Алгоритм что это такое в математике

Алгоритмы в математике

Разделы: Математика

Современные формы обучения, инновации в преподавании, введение новых технологий диктуют учителю необходимость постигать секреты мастерства, а значит, и совершенствовать методы обучения и воспитания учащихся.

Исследования психологов и педагогов, опыт коллег показывают: чтобы научить детей самостоятельно учиться и проявлять творчество необходимо применение деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и обучить их приемам и способам учебной деятельности, которые помогут сформировать необходимые знания, умения и навыки.

Курс школьной математики имеет достаточно широкие возможности для применения различных приемов, методов и технологий. В последние годы в содержание школьного курса естественным образом закладывается алгоритмическая линия. Так как применение алгоритмов является приоритетным в моей работе, то нужно отметить что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть принципиальные отличия, а именно:

– прием – это рациональный способ работы, который состоит из отдельных действий, он может быть выражен в виде правил или инструкций, его можно перестроить и на его основе создать новый прием. Приемы деятельности допускают самостоятельный выбор учениками конкретных действий по решению учебных задач;
– алгоритм – это общепонятное и однозначное предписание, которое определяет последовательность действий, позволяющее достичь искомый результат. Алгоритм предполагает жесткое выполнение шагов, а прием дает общее направление деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование приемов решения задач. Школьные задачи делятся на: алгоритмические, полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи предполагает свои схемы решения, подходы, применение логики и изобретательности.

На начальном этапе обучения математике применение алгоритмов способствует формированию и прочному усвоению навыков владения математическими методами. Также осуществляется подготовка к формированию первоначальных представлений о математическом моделировании. Уже в начальных классах прослеживается применение простейших алгоритмов выполнения арифметических операций, дети овладевают навыками выполнения последовательных действий. Решают задачи с составлением схем и кратких записей. Это можно рассматривать как пропедевтику операционного стиля мышления.

Следующий уровень алгоритмической культуры учащихся – введение понятия алгоритма и формирование его основных свойств. Это происходит в среднем звене школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его правильной речью. У учителя появляется возможность предлагать задачи с элементами творчества. А материал, предлагаемый в наших школьных учебниках, является хорошей базой для обучения составлению простейших алгоритмов и дальнейшей их записи в разных формах. Мы применяем табличную, графическую (блок-схема), словесную и формульную форму записи алгоритмов.

В качестве примера, иллюстрирующего процесс алгоритмизации как средство обучения, можно указать на решение задач методом уравнений. Примером графического алгоритма является блок-схема для отыскания количества решений системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).

Отыскания числа решений системы двух линейных уравнений (блок-схема)

Рис. 1
Графические алгоритмы

Табличную форму алгоритма можно продемонстрировать на примере таблицы, составляемой для исследования функций и дальнейшего построения графиков (см. рис. 2).

Исследование функции и построение графика

Функция задана уравнением у = f(x). Исследовать функцию и построить ее график.

1. Таблица исследования функции

2. Построение графика

Рис. 2
Табличный алгоритм

Пример формульного способа – последовательность нахождения компонентов при составлении уравнения касательной к графику той или иной функции (см. рис. 3).

Уравнение касательной к графику функции

Рис. 3
Формульный способ

Словесный алгоритм используется практически во всех правилах выполнения действий, например, правило сложения чисел с разными знаками (см. рис. 4).

Алгоритм сложения чисел с разными знаками

Рис. 4
Словесный алгоритм

В старших классах работа становится разнообразней и содержательней, появляется возможность включать упражнения разного типа и уровня сложности, предполагающее, что приемы деятельности могут быть разной степени сложности и обобщенности. Они состоят из большого числа действий, выполнение которых приводит к применению алгоритмов на отдельных этапах работы.

Такой подход к преподаванию математики в основной школе определяет условия для формирования у учащихся навыков, позволяющих в старших классах успешно изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших классах, по мнению некоторых учителей, отбивает творческий подход к решению задач, но с другой стороны, твердое знание основных задач курса и умение их решать, является твердым фундаментом для активизации самостоятельной и творческой работы учащихся.

Источник

Что такое алгоритм

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В интернете очень часто встречается слово «алгоритм», и для многих оно является загадкой.

Разберемся на понятных и простых примерах с понятием алгоритма (что такое), а также с его видами и применением.

Алгоритм — это.

Алгоритмы окружают нас повсюду. По их принципам существует животный мир, люди, работают компьютеры и механизмы. Некоторые из них очевидны, другие же скрыты от глаз (но это не значит, что их нет).

Алгоритм в информатике — это последовательность действий, которая направлена на достижение окончательного решения проблемы наиболее оптимальными и эффективными способами.

Существует версия, что термин алгоритм произошел от имени древнего ученого Аль-Хорезми, который написал трактат «Книга о сложении и вычитании».

Позднее один из переводчиков на латинский язык неправильно перевел имя ученого и вынес его в название книги — «Алгоритмии о счете индийском». Так этот термин проник в европейские языки и закрепился в них.

Существуют сложные и легкие алгоритмы. Для решения одних не требуется усилий, а для других не хватит и всей мощности компьютеров.

Любые действия, предполагающие определенную последовательность в жизни животных и людей, можно назвать алгоритмом (поиск пищи для животного, поход в магазин за хлебом).

Конечно, животное, ищущее корм, не подозревает, что использует алгоритмы, но действует по определенным правилам (инстинктам), чтобы добыть пропитание:

В информатике и программировании алгоритмы используются для написания программ (что это такое?). Чем качественнее алгоритмы, используемые в программе, тем лучше она работает.

Когда вы начинаете изучать любой язык программирования, то первое, что вам объясняют — это принципы построения алгоритма для будущей программы. Это такие блок-схемы, которые наглядно покажут ход обработки данных и логику вычислений. Без них поначалу будет очень трудно писать программы.

Как все это делается и выглядит на практике отлично показано на приведенном выше видео. Не буду повторяться, а лишь настоятельно посоветую потратить десять минут на его просмотр.

Виды и типы алгоритмов

Линейный алгоритм — это последовательное выполнение инструкций в строгой очередности их расположения (пример, «сделать бутерброд с сыром»).

Ветвления — последовательность действий в соответствии с определенными условиями (если одно условие, то выполняется действие 1, если другой условие, то выполняется действие 2);

Пример: Если идет сильный дождь, тогда возьми зонт, а иначе брать зонт не нужно.

В большинстве случаев слово «иначе» опускается, так как из контекста первой части фразы уже понятна дальнейшая логика.

Пример: Если хотите сообщить что-то важное, позвоните по телефону (в данном случае, очевидно, что если сообщение неважное, то звонить не нужно).

Циклические алгоритмы — это последовательность действий, которую необходимо повторять несколько раз для достижения положительного результата («проверка груш на гнилые и не гнилые»).

Пример: В одном ящике лежат груши, необходимо отобрать гнилые и хорошие. Для этого совершаем следующие действия:

Иногда случаются ситуации, когда цикл начинает бесконечно повторяться. Это называется зацикливанием или бесконечный цикл.

Это происходит в том случае, когда условие не может быть выполнено, тогда цикл замыкается в бесконечное повторение. Стоит отметить, что таких ситуаций следует избегать.

В языках программирования существуют различные виды алгоритмов для решения определенных задач.

К основным видам, которые должен знать каждый начинающий программист, можно отнести те, которые используют методы сортировки и поиска.

Все, что нас окружает построено именно на этих алгоритмах, они считаются простыми для понимания.

Где применяют алгоритмы

В математических науках и информатике это поиск эффективного решения поставленной задачи с использованием инструментов и средств.

Например, даже при решении простой задачки (2 * 6) используются определенные методы и инструменты для получения правильного результата. Самое интересное заключается в том, что ее можно решить несколькими способами: использовав листок и ручку, посчитав на компьютере или выполнив умножение в уме. Наиболее эффективный способ решения этой задачи и будет лучшим алгоритмом в данном случае.

Но такие простые примеры не очень интересны для любителей информатики. Есть гораздо более захватывающие проблемы, волнующие умы многих программистов, и над их решением бьются ученые всего мира.

Задача продавца (коммивояжера)

Существуют более интересные примеры для понимания сложности функционирования алгоритмов. Например, задача коммивояжера.

Дано: одному продавцу необходимо посетить четыре города: например, Москву, Берлин, Лондон, и Сан-Франциско. Продать там товар, а затем вернуться обратно.

Решение задачи выглядит простым. Сначала из Москвы поехать в Берлин, затем посетить Лондон, а потом отправиться в Сан-Франциско и вернуться в Москву.

На самом деле это сложный для компьютера алгоритм. В этих 4-х вариантах скрыто 24 различных комбинаций путешествия для решения задачи. Компьютер высчитывает расстояние от одного города до другого, затем сравнивает варианты и выдает решение.

Но если увеличить количество городов (например, до 100), то компьютер не сможет решить эту задачу, так как вариантов будут миллионы, а на решение понадобится несколько веков.

Но самым интересным является то, что, поняв принцип решения подобной задачи, его можно распространить на все подобные, что расширит знания в области информатики (это что?) и других наук.

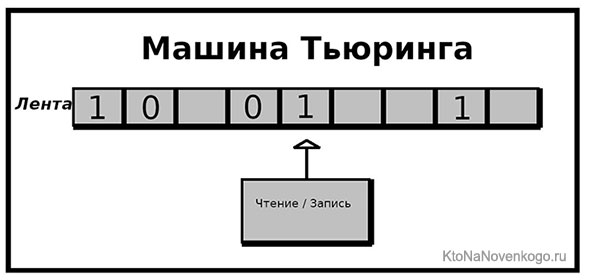
Машина Тьюринга — это основа для понимания алгоритмов

Это абстрактная машина, которую придумал Алан Тьюринг, известный британский ученый. Гениальность этого автомата состоит в следующем. Есть некая лента, состоящая из множества отдельных (бесконечных) ячеек, в которых содержатся данные или биты (0 и 1). Есть считывающее устройство, имеющее доступ к ленте.

В процессе движения устройство снабжено определенными инструкциями, получает доступ к ячейкам, считывает информацию и шагает дальше. Но машина может изменять свои действия, записать другую информацию или передвигаться то в одну, то в другую сторону (на основе стека внутренних инструкций).

В результате исследований таких машин Тьюрингом выдвинута гипотеза о том, что алгоритм при нахождении значений некоторой функции, которая задана в области алфавита, только тогда существует, когда данная функция вычисляется на машине Тьюринга.

Это аксиома, постулат, которые невозможно доказать математическим методом, так как алгоритм — это не точное математическое понятие.

Заключение

Изучение алгоритмов — это важная часть в понимании работы компьютеров. Оно позволяет узнать, как компьютер функционирует, как принимает, обрабатывает данные и выдает необходимый результат.

Понимание принципов работы поможет лучше овладеть компьютерными языками, так как, владея принципами построения и создания эффективных алгоритмов, можно изучить любой язык программирования (как алфавит в иностранных языках).

Изучаете, осваивайте, применяйте алгоритмы. Надеемся, что наша статья помогла вам в этом!

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (7)

Даже не прочитав статью, а прочитав название, сразу ответил правильно на вопрос. Алгоритм — это реально любая последовательность действий, которая позволит достичь цели.

Можно представить даже поход на работу в виде алгоритма. Если вышли вовремя, то идем на трамвай допустим, если опаздываем, то вызываем такси, если погода хорошая, то берем зонтик / не берем и т.д.

Все программирование в принципе построено на алгоритмах.

Чтобы разобраться с алгоритмами в написании программ нужно иметь хорошо развитое логическое мышление, для программиста главное орудие — это не математика, а именно логика.

Проблема ведь и кроется в том, что поменяв местами две инструкции, синтаксис языка программирования не будет нарушен, но будет нарушена логика, и это нарушение компилятор спокойно пропустит. Вот из-за таких логических ошибок и появляются баги в программах.

Я бы не сказал, что бесконечный цикл в программировании нужно избегать, тут всё от задумки программиста зависит. Если мы хотим, чтобы программа начиналась снова и снова, то тут и нужен бесконечный цикл, а выход из него можно предусмотреть с помощью ветвления if и else и оператора break.

Для успешного программирования нужно обладать хорошей логикой, ведь любой алгоритм опирается на логику, а не существует сам по себе.

Я заметил, что многие алгоритмы я не пропускаю через своё сознание, а выполняю их на уровне рефлекса, к примеру, сначала надеваю кофту, а на неё уже куртку, а не наоборот. Все простые алгоритмы именно так и выполняются, без включения осознанности.

Блок-схема — это слишком общий алгоритм, с его помощью можно понять лишь самую общую логику работы программы. Для написания программы этой схемы недостаточно.

Источник

Алгоритмы

Чтобы успешно применять современный анализ данных, нам нужно познакомиться с понятием алгоритма. Алгоритм – это основное понятие математики и современного анализа данных.

Под алгоритмом понимается набор последовательных действий, которые направлены на достижение определенной цели.

Алгоритмы используются не только в математике, но и во всех областях человеческой деятельности, даже часть творческой работы, например, создания скульптуры или картины, может быть алгоритмизирована, что мы наблюдаем в классических академических работах.

Лучше всего познакомиться с понятием алгоритма на примерах.

Мы начнем с классического примера – алгоритма Евклида.

Алгоритм Евклида

Пусть у вас имеется два натуральных числа a и b, например, 2014 и 15. Ваша цель – найти наибольший общий делитель этих чисел.

Итак, нужно найти делитель, который должен быть, во-первых, общим для двух чисел, во-вторых, максимальным.

Очевидно, различных задач такого типа существует столько, сколько различных пар чисел а, b.

Нам необходимо найти последовательность действий, пригодную для всех натуральных чисел a и b.

Попробуем осмыслить задачу и понять, как Евклид пришел к этому алгоритму.

Очевидно, вначале он обозрел два числа и предположил, что одно из них больше другого, например, a > b.

Далее можно предположить, что b является таким делителем.

Вопрос: как это проверить?

Деление – это обобщение вычитания, поэтому будем из числа a последовательно вычитать число b. Сделаем это несколько раз подряд, пока не получим 0.

Если получили 0, то решение найдено, b и есть искомый наибольший делитель.

Но пусть 0 не найден, а на определенном шаге у нас получается остаток – число b1 меньшее b, и мы не знаем, что делать дальше.

Разумно сосредоточиться на этом остатке.

У нас возникает предположение, что если есть общий делитель, то он должен находиться именно в этом остатке b1.

Задача. Попробуйте доказать, что это действительно так!

Поэтому мы можем продолжить наши действия с остатком b1, вычитая его из числа a, и повторить эту процедуру несколько раз.

В итоге мы придем к заключению: либо общего делителя нет, либо найдем максимальный делитель двух чисел, процесс оборвется на конечном числе шагов.

Мы применили эти действия к двум числам, предполагая, что a > b.

Если это неравенство не выполняется, мы просто меняем числа местами и достигаем поставленной цели.

Конечно, это не единственный способ нахождения максимального делителя, мы могли бы предложить простой перебор, последовательно подставляя числа от 1 до b и проверяя, делят они нацело исходные числа или нет.

Очевидно, алгоритмы можно сравнивать по числу операций или усилий, которые вы затратили на достижение своей цели, а также на объем затраченных ресурсов.

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к четырем арифметическим действиям, называются численными алгоритмами.

Они играют важную роль в самых разнообразных областях математики.

Например, пусть нужно решить систему двух уравнений первой степени с двумя неизвестными:

Алгоритм решения этой системы дается формулами

которых полностью выражен как состав действий, так и порядок их выполнения.

В приведенных формулах предусмотрена одна и та же цепочка действий для всех задач данного типа (т. е. при любых коэффициентах ).

Конечно, нам нужно предположить, что знаменатели не обращаются в 0.

Можно написать последовательность действий, рассматривающую все варианты значений коэффициентов уравнений. Можно также по шагам исключить одно неизвестное, найти значение другого, как это делается в школе. Именно важен сам принцип алгоритмистики.

Интересно, заметить, что, вообще говоря, число операций, предписываемых алгоритмом, заранее не бывает известным; оно зависит от конкретного выбора условий задачи и выясняется в процессе решения.

В частности, так обстоит дело и в случае алгоритма Евклида, где число вычитаний, которые могут понадобиться, зависит от выбора той или иной пары чисел а, b.

Точное число операций можно оценить и выбрать алгоритм с наименьшим числом операций или обладающий другими оптимальными свойствами, например, по количеству требуемой памяти.

Широкое распространение численных алгоритмов обусловливается тем, что к четырем арифметическим действиям можно свести многие другие операции.

Правда, такое сведение обычно не является исчерпывающе точным, но оно может быть осуществлено с любой наперед заданной точностью.

Все это можно было бы иллюстрировать на примере алгоритма извлечения корня квадратного, который позволяет находить корень приближенно, но с любой наперед заданной точностью, при помощи последовательности делений, умножений и вычитаний.

В специальной ветви современной математики (численные методы) разрабатываются аналогичные приемы сведения к арифметическим действиям и более сложных операций, как интегрирование, дифференцирование и т. д.

В математике серия задач определенного типа считается решенной, когда для ее решения установлен алгоритм. Нахождение таких алгоритмов является естественной целью математики.

Например, в алгебре установлены алгоритмы, которые по заданным коэффициентам алгебраического уравнения позволяют совершенно автоматически определить, сколько различных корней имеет данное уравнение (и какой кратности), и вычислить эти корни с любой наперед заданной точностью.

Если же математик не обладает алгоритмом для решения всех задач данного типа, то хотя порою и удается решать некоторые единичные задачи этого типа, но в отдельных случаях приходится придумывать специальную процедуру, непригодную уже для большинства других случаев.

Примеры

Приведем пример такого класса однотипных задач, для решения которых современная математика не располагает алгоритмом.

Рассмотрим всевозможные диофантовы уравнения, т. е. уравнения вида

где P является многочленом с целочисленными коэффициентами.

Уравнения названы в честь древнегреческого математика Диофанта. Диофа́нт Александри́йский — древнегреческий математик, живший предположительно в III веке н. э.

Основное произведение Диофанта — Арифметика в 13 книгах, из которых сохранились только 6 первых книг из 13.

Примеры диофантовых уравнений:

из которых первое — с двумя неизвестными, а второе с одним неизвестным (вообще же рассматриваются уравнения с любым числом неизвестных).

Уравнение может иметь целочисленное решение, а может и не иметь его.

Первое из приведенных уравнений имеет целочисленное решение

Второе уравнение не имеет целочисленного решения, ибо для любого целого х легко устанавливается неравенство

В 1901 году немецкий математик Давид Гильберт огласил список 20 трудных задач, среди них была и такая задача:

требуется выработать алгоритм, позволяющий для любого диофантова уравнения выяснить, имеет ли оно целочисленное решение.

Позднее эту задачу Гильберта решали многие математики, заключительное доказательство принадлежит советскому математику Ю.В.Матиясевичу (см. Ю. В. Матиясевич Диофантовость перечислимых множеств // Доклады Академии наук СССР. — 1970. — Т. 191. — № 2. — С. 279—282).

Ю. В. Матиясевич Десятая проблема Гильберта. — М.: Наука: Физико-математическая литература, 1993. — 223 с. — (Математическая логика и основания математики; выпуск № 26). —ISBN 502014326X

Для частного случая диофантова уравнения с одним неизвестным такой алгоритм известен.

с целочисленными коэффициентами.

Алгоритм нахождения такого корня простой: нужно перебрать все делители свободного члена приводит к цели:

Отметим общие свойства алгоритмов.

Требуется, чтобы метод вычисления можно было сообщить другому лицу в виде конечного числа указаний, как следует действовать на отдельных стадиях вычисления.

При этом вычисления согласно этим указаниям не зависят от произвола вычисляющего лица и представляют собою определенный процесс, который может быть в любое время повторен и выполнен другим человеком.

Алгоритм решает не индивидуальную задачу, а решает множество однотипных задач.

Далее мы используем отрывки из увлекательной книги Б.А.Трахтенброта Алгоритмы и машинное решение задач и расскажем о некоторых интересных алгоритмах.

Задача Тезея и алгоритм поиска чудовища

Греческая мифология повествует о легендарном герое Тезее, который отважился проникнуть в лабиринт для того, чтобы разыскать в нем чудовищного Минотавра. Ему помогла выбраться из лабиринта Ариадна, давшая Тезею клубок ниток, один конец которых держала она сама. По мере углубления Тезея в лабиринт клубок разматывался; наматывая потом нитки, Тезей благополучно вернулся к выходу.

Об этой древней легенде напомнила автоматическая игрушка «Мышь в лабиринте», созданная американским математиком и инженером Клодом Шэнноном.

В одном месте специального лабиринта ставится вещь, условно именуемая куском сала, в другом — «мышь». Мышь начинает блуждать по лабиринту, делая при этом петли, пока находит «сало». Если повторно запустить «мышь» с того же места, то она уже прямо бежит к «пище», не делая петель.

Лабиринт можно представить в виде конечной системы площадок, от которых расходятся коридоры, причем каждый коридор соединяет две площадки (такие площадки будем называть смежными), но не исключается существование таких площадок, из которых можно пройти только в один коридор (такие площадки будем называть тупиками).

Будем говорить, что площадка Y достижима из площадки X, если существует путь, ведущий от X к Y через промежуточные коридоры и площадки.

Точнее это означает, что либо X и Y—смежные площадки, либо существует последовательность площадок таких, что X и , и , и . и т. д. и, наконец, и Y смежны.

Например, на, рис. 1 площадка H достижима из тупика A посредством пути АВ, ВС, CD, DE, EF, FD, DH, в то время как площадка K не достижима из А.

Вместе с тем, если K вообще достижима из X, то она достижима и посредством простого пути, т. е. такого пути, в котором каждая площадка (а тем более и каждый коридор) проходится лишь один раз.

В предыдущем примере пусть и не был простым, но, срезав петлю DB, EF, FD, мы получаем простой путь АВ, ВС, CD, DH.

Предполагается, что Минотавр находится на одной из площадок лабиринта (обозначим ее через М), а Тезей, отправляясь на его поиски с площадки А, на которой его ждет Ариадна.

Герой должен решить следующую задачу: достижим минотавра M из A или нет.

Если Минотавр достижим, то нужно добраться до него по какому бы то ни было пути, но вернуться к Ариадне нужно уже по простому пути (не делая петель).

Если же М не достижима, то вернуться к Ариадне.

Различных лабиринтов может быть бесчисленное множество, а взаимное расположение в данном лабиринте площадок А и М также можно варьировать.

Поскольку Тезею заранее ничего не известно об устройстве данного лабиринта и о местонахождении в нем Минотавра, то решение поставленной задачи мыслится в виде общего метода поисков пригодного при любом лабиринте и при любом расположении в нем площадок А и М.

Иными словами, решение мыслится в виде алгоритма, решающего любую из задач данного типа.

Для построения такого алгоритма рассмотрим один специальный метод поисков.

На любой стадии процесса поиска в соответствии с этим методом приходится различать коридоры, еще ни разу не пройденные Тезеем (условно — зеленые), пройденные один раз (желтые), пройденные дважды (красные).

Далее, находясь на какой-либо площадке, Тезей может попасть на одну из смежных площадок посредством одного из следующих ходов:

Предполагается, что Тезей делает какие-то пометки, позволяющие ему впоследствии различать красные коридоры от зеленых; желтые различимы тем, что по ним протянута нить Ариадны.

Выбор того или иного хода зависит от обстановки, наблюдаемой Тезеем на той площадке, на которой он находится в данный момент.

Эту обстановку можно охарактеризовать следующими признаками:

Метод поиска может быть теперь задан следующей схемой:

1МинотаврОстановка2ПетляНаматывание нити3Зеленая улицаРазматывание нити4АриаднаОстановка5Пятый случайНаматывание нити

Находясь на какой-нибудь площадке, Тезей делает очередной ход так: он проверяет по порядку номеров в соответствии с левым столбцом схемы, какой из перечисленных признаков имеет место; обнаружив первый такой признак, он (уже не проверяя остальные признаки) делает соответствующий ход (или остановку) из правого столбца.

Такие ходы делаются до тех пор, пока не наступает остановка.

Пригодность метода непосредственно вытекает из следующих трех утверждений:

Прежде чем доказывать эти утверждения, покажем на двух примерах, как работает метод.

Пример 1

Пусть с площадки А лабиринта (рис. 1) начинается поиск Минотавра, который находится в F.

Процесс поиска в соответствии с нашим методом удобно изобразить посредством схемы (в силу произвола при выборе зеленого коридора — это лишь одна из возможных схем), представленной на таблице 2.

Каким признаком руководствуется Тезей

Цвет коридора после его прохождения

1Зеленая улицаРазматывание нитиABЖелтый2Зеленая улицаРазматывание нитиBCЖелтый3Зеленая улицаРазматывание нитиCDЖелтый4Зеленая улицаРазматывание нитиDHЖелтый5Зеленая улицаРазматывание нитиHJЖелтый6Пятый случайНаматывание нитиJHКрасный7Пятый случайНаматывание нитиHDКрасный8Зеленая улицаРазматывание нитиDBЖелтый9ПетляНаматывание нитиBDКрасный10Зеленая улицаРазматывание нитиDFЖелтый11МинотаврОстановка..

Мы видим, что в данном случае Минотавр достижим. Выделив в предпоследнем столбце те из коридоров, которые остались желтыми (в соответствии с показаниями последнего столбца), получим следующий простой путь, ведущий от A к F:

Пример 2

Если же поиск начинается с площадки K, то процесс поиска можно изобразить в схеме, представленной на таблице 2.

Мы видим, что в этом случае Минотавр не достижим.

Перейдем теперь к доказательству утверждений 1—3.

Доказательство утверждения 1.

Покажем методом индукции по числу ходов Тезея, что на любом этапе процесса поиска возникает следующая альтернатива (т. е. имеет место один из следующих двух случаев, взаимно исключающих друг друга):

Каким признаком руководствуется Тезкй

Цвет коридора после прохождения

1Зеленая улицаРазматываниеKNЖелтый2Зеленая улицаРазматываниеNLЖелтый3Зеленая улицаРазматываниеLMЖелтый4Зеленая улицаРазматываниеMNЖелтый5ПетляНаматываниеNMКрасный6Пятый случайНаматываниеMLКрасный7Пятый случайНаматываниеLNКрасный8Пятый случайНаматываниеNKКрасный9АриаднаОстановка..

a) В лабиринте нет желтых коридоров; при этом Тезей находится на площадке А (Ариадны).

b) В лабиринте имеются желтые коридоры, причем они, будучи рассмотрены в том порядке, в каком они были пройдены Тезеем, образуют путь, ведущий от А до площадки, на которой находится Тезей.

Вместе с тем будет обнаружено, что Тезей никогда не проходит по красному коридору.

Высказанные положения являются очевидными для начала процесса, когда Тезей еще находится на площадке А и никакой коридор еще не пройден (все коридоры — зеленые). Предположим теперь, что указанные альтернативы справедливы после (n—1)-го хода и покажем, что тогда они справедливы и после n-го хода (разумеется, если только (n— 1)-й ход еще не привел к остановке).

Пусть после (n— 1)-го хода имеет место случай а.

Тогда очередной ход может быть либо продвижением по зеленому коридору от А до некоторой смежной площадки K (после n-го хода возникает случай б с единственным желтым коридором AK), либо остановкой на площадке А (после n-го хода сохраняется случай a). Допустим теперь, что после (n— 1)-го хода имеет место случай б с s желтыми коридорами, образующими путь .

В зависимости от того, каким признаком руководствуется Тезей при выборе очередного n-го хода, после n-го хода имеются следующие возможности:

Таким образом, полностью установлена упомянутая выше альтернатива, а также выяснено, что по каждому коридору Тезей проходит не более двух раз (по красному он никогда не проходит).

Поскольку, кроме того, число всех коридоров в лабиринте конечно, то и последовательность ходов должна быть конечной; но эта последовательность может оборваться только при остановке Тезея на площадке Минотавра или на площадке Ариадны.

Доказательство утверждения 2. В случае остановки на площадке Минотавра факт достижимости очевиден, причем нить Ариадны протянута вдоль желтого пути, существование которого было установлено выше.

Отсутствие петель в нити обеспечивается тем, что каждый раз, когда в процессе блуждания Тезей обнаруживает петлю, он возвращается обратно и тем самым ликвидирует ее.

Доказательство утверждения 3. Заметим, что в случае остановки на площадке Ариадны

Предположим теперь от противного, что Минотавр достижим и пусть —путь, ведущий от А к М.

Первый коридор в этом пути является красным, ибо он выходит из А, последний же является зеленым, ибо Тезей в своих поисках до Минотавра не добрался. Пусть — первый зеленый коридор в этой последовательности.

Таким образом, к примыкают зеленые и красные коридоры.

Рассмотрим теперь последнее прохождение Тезея через площадку ; оно, очевидно, произошло по одному из красных коридоров, примыкающих к

Однако последнего быть не может, ибо из выходит зеленый коридор .

Поэтому приходится допустить, что последнее прохождение через было связано с обнаружением петли. Однако это немедленно приводит к противоречию, чем и завершается доказательство утверждения 3.

Именно, если бы в была обнаружена петля, то это означало бы, что из нее выходят по крайней мере два желтых коридора; сделав свой очередной ход, Тезей превратил бы один из этих желтых коридоров в красный, оставшийся же желтый коридор должен быть обязательно пройден впоследствии повторно, ибо желтых коридоров не должно оставаться; тогда же будет пройдена еще раз площадка .

Это противоречит допущению, что рассматривается последнее прохождение через .

Сделаем теперь следующее замечание. В предложенном нами предписании для поиска пути допускается известный элемент случайности.

Именно, при условии зеленая улица очередной ход не определен однозначно, поскольку с данной площадки могут оказаться выходы в несколько зеленых коридоров, а наше предписание не предусматривает, какой из них нужно выбрать, точнее — оно допускает произвольный случайный выбор одного из них.

Тем самым нарушается свойство детерминированности, о котором в предыдущем параграфе говорилось, что оно присуще всем алгоритмам.

Этот элемент случайности можно устранить (и тем самым превратить рассмотренное предписание в алгоритм) хотя бы соглашением, что при наличии нескольких зеленых коридоров выбирается коридор по некоторому правилу.

Например, выйдя на площадку, Тезей начинает ее обходить по часовой стрелке до появления первого зеленого коридора и далее следует по нему, или же каким-нибудь другим соглашением.

Вывод

Рассмотрение таких предписаний, в которых заранее предусматриваются акты случайного выбора, представляет большой теоретический и практический интерес, особенно в теории игр. В таких задачах мы видим соединение теории алгоритмов и теории вероятностей.

Источник