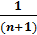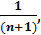Аликвотные дроби что это
Тема «Аликвотные дроби» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Аликвотные дроби
Происхождение аликвотных дробей.
Тема «Аликвотные дроби» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби.
Египтяне ставили иероглиф «Глаз Хора»
Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить «хекат», основную меру объёма в Древнем Египте, т.е.аликвотные дроби нужны были египтянам в практических целях.
вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
Основные операции над аликвотными дробями
Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Скажем, число 2/43 выражается так: 2/43= 1/42 +1/86 +1/129 +1/301.Производить арифметические действия над числами, раскладывая их в сумму долей единицы, очень неудобно.
Поэтому в процессе решения задач для разложения аликвотных дробей в виде суммы меньших аликвотных дробей возникла идея систематизировать разложение дробей в виде формулы. Эта формула действует, если требуется разложение аликвотной дроби на две аликвотные дроби.
Формула выглядит следующим образом:
Примеры разложения дробей:
Но если преобразовать нашу формулу, то получим следующее полезное равенство:
Т.е. аликвотную дробь можно представить разностью двух аликвотных дробей, или разность двух аликвотных, знаменателями которых являются последовательные числа равна их произведению.
Вернемся к формуле и докажем это равенство:
( n+1 )/((n+1)*n) после сокращения получаем:
Итак, получается, что 1/n=1/n. Наша формула верна.
Но мы пойдем дальше, и на основании разности аликвотных дробей решим, на первый взгляд, трудноразрешимую для обычного человека задачу:
Воспользуемся нашей формулой для разложения аликвотной дроби в виде разности:
Подставив, уже разложенные выражения в наш пример, получаем:
Мы представили формулу, как удобство при разложении аликвотной дроби на 2 слагаемых. При разложении 1 на два слагаемых получается:
1=1/2+1/2 (Наша формула действует!). Чтобы разложить 1 на 3 слагаемых, мы возьмем одну аликвотную дробь и по формуле разложим ее еще на две аликвотные дроби:
Чтобы разделить на 4 слагаемых, делим еще одну дробь на две аликвотные дроби:
На 5 слагаемых: 1/6=1/7+1/42 => 1=1/2+1/4+1/12+1/7+1/42.
Решение задач из учебника
Б) четырех слагаемых
Если 1/n написало лучше, а 1/(n-1) хуже. В идеале никто не написал работу также как и он, но с таким же результатом могло быть и большее количество учеников.
За нескольких сказать ничего не могу, а за одного: Мы можем взять число всех учеников классе за 1. И тогда получается что мы должны разложить число 1 на 3-и аликвотные дроби.
1/x=1/n*(n-1) тогда получается что в классе n*(n-1) учеников.
Методом подбора мы видим что 1 раскладывается на аликвотные дроби только следующим образом :
1=1/2+1/2=1/2+1/3+1/6 во всех других случаях мы не сможем получить из суммы других аликвотных дробей 1.
А если таких учеников было несколько, то задача имеет множество решений.
Решение олимпиадных задач
Задача. Найди сумму
Чтобы найти решение данной задачи необходимо найти сумму
И вычесть из нее сумму
Задача. Найти сумму
1, b) 10/11, c) 4/5, d) 8/9, e) 9/10
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2013*2014) умножить на год проведения зимних олимпийских игр в городе Сочи.
2013/2014 * 2014 = 2013
Ответ : Универсиада будет проводиться в 2013 году.
Аликвотные дроби что это
Чтобы найти решение данной задачи необходимо найти сумму
И вычесть из нее сумму
Таким образом, при разработке данной темы, я узнала, что первыми дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.
Решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Поэтому решения задач с применением аликвотных дробей – это занимательный процесс, развивающий мышление и логику, который помогает решать нестандартные и олимпиадные задачи по математике разных лет.
Список использованных источников и литературы
Петерсон Л. Г. Математика, 5класс. – М.:Ювента, 2016.
Фарков А. В. Математические олимпиады в школе, 5-11классы. – М.: Айрис-пресс, 2012.
Фарков А.В. Математические олимпиады 5-6 классы.- М: Издательство «Экзамен». – М.:2019
Энциклопедический словарь юного математика для среднего и старшего школьного возраста, М.: Педагогика,1989.
Аликвотные дроби что это
Тема «Аликвотные дроби при решении нестандартных задач» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби.
· Выяснить, какое значение имеют аликвотные дроби в нашей жизни.
· Узнать происхождение аликвотных дробей.
· Рассмотреть основные операции с аликвотными дробями.
· Решать олимпиадные задачи с помощью аликвотных дробей.
· Составлять и решать задачи практического содержания.
История аликвотных дробей
Аликвотная дробь- дробь, числитель которой равен единице.
Аликвотные дроби начали использоваться ещё в древности. Необходимость в дробных числах возникла в результате практической деятельности человека. Потребность в нахождении долей единицы появилась у наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения. [8]
Первые дроби, с которыми нас знакомит история, это дроби вида – 1/2, 1/3, 1/4 – так называемые единичные дроби, так как числитель этих дробей единица. Причиной появления этих дробей являлась необходимость разбить единицу на доли. Это нужно было для того:
1. чтобы разделить добычу после охоты, ведь, нужно было знать, сколько частей составляет целое и кому какая часть добычи станет принадлежать.
2. выразить результат измерения длины, времени, площади, массы и вести расчеты за товары
Аликвотные дроби в Древнем Египте
Аликвотные дроби появились раньше других дробей. В Древнем Египте математики «настоящими» считали только аликвотные дроби вида 1/n.
Итак, дроби вида 1/n, где числитель 1, а n – натуральное число, (т.е. число, которое используется для счёта предметов), называются аликвотными дробями (от латинского aliguot-« несколько») или единичными.[2]
В Древнем Египте «настоящими», математики, считали только аликвотные дроби. Поэтому каждую дробь стремились представить в виде суммы меньших аликвотных дробей, причём с разными знаменателями.
Кроме того, для единиц измерения емкостей и объемов использовался так называемый глаз «Хора»
Он представлял собой дробь 63/64.
Так как, согласно мифам глаз Хора был выбит, а затем восстановлен на 63/64. Каждая часть глаза соответствовала определённой дроби и была представлена в виде суммы аликвотных дробей таким образом:
Аликвотные дроби встречаются в древнейших, дошедших до нас математических текстах, составленных более 5000 лет тому назад, – древнеегипетских папирусах и вавилонских клинописных табличках. Они нужны были для практических целей.[8]
Рассмотрим такую задачу: «Разделить 7 хлебов между 8 людьми» Если разрезать каждый хлеб на 8 частей, придется провести 49 разрезов (7 хлебов по 7 надрезов в каждом хлебе). А по-египетски эта задача решалась так:
Значит, каждому человеку нужно дать половину хлеба, четверть хлеба и восьмушку хлеба. При этом, придется сделать почти в три раза меньше разрезов.
Значение аликвотных дробей в истории:
Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка «Попасть в дроби», что означало оказаться в трудном положении.
Формулы аликвотных дробей
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Сюда относятся, прежде всего задачи, в которых требуется разделить какие-либо ресурсы на несколько частей с наименьшим количеством действий. Для этого необходимо представить какое-либо число в виде суммы аликвотных дробей.[1]
Например: 1/3 = 1/4+1/12,
Из данных примеров следует, что знаменатель первой дроби на 1 больше знаменателя данной дроби. Произведение же знаменателя первой дроби и знаменателя данной дроби соответствует знаменателю второй дроби.
Где n – знаменатель данной дроби является натуральным числом, тогда мы можем представить формулу в таком виде как:
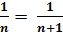
Доказать это равенство можно, приведя дроби к общему знаменателю и после сокращений увидеть, что формула верна.
Кроме того, следует отметить, что аликвотные дроби можно как складывать, так и вычитать.
Поэтому, разложить в виде суммы двух аликвотных дробей можно по формуле:

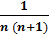
Если преобразовать формулу 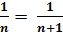
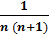
то получим следующие равенства:
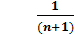
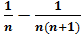
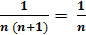
Если разложить в виде разности двух аликвотных дробей по формуле: 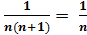
то мы увидим, что аликвотную дробь можно представить разностью двух аликвотных дробей, знаменателями которых являются последовательные числа равные их произведению.
Так, например: 1/6 = 1/(2*3) = 1/2-1/3
Решение нестандартных задач
№1. Представить число 1 в виде сумм различных аликвотных дробей.[5]
б) четырёх слагаемых:
№2. Представьте дробь 1/2020 в виде аликвотных дробей.[7]
Это, опять-таки, из-за простоты числа 2020.
№3. Найти сумму аликвотных дробей[6] 1/2+1/((2*3))+1/((3*4))+1/((4*5))+?+1/((19*20))
Решение: воспользуемся формулой для разложения аликвотной дроби в виде разности
Подставив, уже разложенные выражения в сумму, получим:
№4. Найти сумму аликвотных дробей [6] 1/20+1/30+1/42+1/56+1/72+1/90+1/110+1/132
Решение: воспользуемся формулой для разложения аликвотной дроби в виде разности
1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10+1/10-1/11+1/11-1/12=1/4-1/12= (3-1)/12=2/12=1/6 1/20+1/30+1/42+1/56+1/72+1/90+1/110+1/132=1/6
№5. Решить уравнение [4]
(1/(25*26)+1/(26*27)+1/(27*28)+1/(28*29)+1/(29*30))*150+1,03:[10,3*(х-1)]=11 Решение: упростим уравнение и найдем сумму аликвотных дробей: 1/(25*26)+1/(26*27)+1/(27*28)+1/(28*29)+1/(29*30)
Представим каждую дробь в виде разности аликвотных дробей
После нахождения суммы, уравнение примет следующий вид
Чтобы найти решение данной задачи необходимо найти сумму
И вычесть из нее сумму
Таким образом, при разработке данной темы, я узнала, что первыми дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.
Решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Поэтому решения задач с применением аликвотных дробей – это занимательный процесс, развивающий мышление и логику, который помогает решать нестандартные и олимпиадные задачи по математике разных лет.
НЕСКОЛЬКО СЛОВ ОБ АЛИКВОТНОЙ ДРОБИ
Аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек. С Древних времен эта тема считалась одной из самых сложных поэтому, когда человек попадал в трудное положение, говорили «Попал в дроби».
В современной записи этот алгоритм можно представить в виде формулы:
Она действует только тогда, когда требуется разложить аликвотную дробь на две составляющие. Если же преобразовать формулу, то можно получить следующее равенство:
Отсюда следует, что аликвотную дробь можно представить в виде разности двух аликвотных, или же разностью двух аликвотных, знаменателями которых, являются последовательные числа, равные их произведению.
Рассмотрим это равенство, тем самым докажем справедливость данного утверждения:
Приведя дроби к общему знаменателю, получаем:
Рассмотрим задачу на использование метода Фибоначчи.
Чтобы узнать в каком году Фибоначчи со дня рождения исполнится 850 лет, нужно сумму аликвотных дробей
умножить на число, когда Фибоначчи исполнилось ровно 1 год. Если он родился в 1170, прибавляем к этому числу возраст Фибоначчи.
Получается, что Фибоначчи в 2020 году исполняется 850 лет [1].
На современном этапе развития математики ученые продолжают исследовать массу задач, которые связаны с аликвотными дробями. В конце ХХ ученые смогли дать оценку самого большого знаменателя и длины разложения обычной дроби в аликвотную. Также была выдвинута гипотеза Эрдешом и Грэхемом, которые утверждают, что для любой раскладки целых чисел, которые больше единицы в цветов может существовать конечное подмножество S целых. В 2003 году дана гипотеза была доказана известным математиком Эрнестом Крутом.
На сегодняшний день аликвотные дроби ставят для математиков целый ряд трудных и практически нерушимых математических задач. Задачи, связанные с использованием аликвотных дробей в решении, актуальны и в наши дни, так как они составляют обширный класс нестандартных задач. Нужно отметить, что эти задачи являются неотъемлемой частью не только при подготовке к олимпиадам, но также и при подготовке заданий ЕГЭ. Данная тема вляется хорошим подспорьем для исследовательской работы учащихся школ, что повышает успешность обучающихся в учёбе, развивает математические способности, внимание, познавательный интерес к математике.
Список используемых источников
Левитас, Г. Г. Нестандартные задачи по математике./ Г.Г. Левитас. – М.: ИЛЕКСА,2010. – 56 с.
Статья на тему «Аликвотные дроби»
Выяснить, какое значение имеют аликвотные дроби в нашей жизни.
Узнать происхождение аликвотных дробей.
Рассмотреть основные операции с аликвотными дробями.
Решать олимпиадные задачи с помощью аликвотных дробей.
Составлять и решать задачи практического содержания.
Первые дроби, с которыми нас знакомит история, это дроби вида – 
В Древнем Египте «натоящими» математики считали только аликвотные дроби. Поэтому каждую дробь стремились представить в виде суммы меньших аликвотных дробей, причём с разными знаменателями.
при n =5 2/11=1/6 + 1/66 и т.п.
Задачи из журнала «Квант». Решение задач.
Представить число 1 в виде сумм различных аликвотных дробей
Б) четырёх слагаемых:
Представьте дробь 
3. Верно ли равенство?
7.В каком году будет проходить олимпиада в Казани?
Чтобы узнать в каком году в Казани будет проводиться Универсиада нужно сумму аликвотных дробей
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2013*2014) умножить на год проведения зимних олимпийских игр в городе Сочи.
2013/2014 * 2014 = 2013
Ответ: Универсиада будет проводиться в 2013 году.
Олимпиадные задания 2006 – 2007г.
Чтобы найти решение данной задачи необходимо найти сумму
И вычесть из нее сумму
Таким образом, при разработке данной темы, я узнала, что первыми дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.
Таким образом, аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек, а правила действий с произвольными дробями разработаны «сравнительно недавно».
Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.
Левитас Г. Г. Нестандартные задачи по математике.– М.: ИЛЕКСА,2007.
Баженов И.И., Порошкин А.Г. и др. Задачи для школьных математических кружков. Сыктывкар, 1994.
Гаврилова Т. Д. «Занимательная математика». 5-11класс. Волгоград: Учитель, 2008.
Фарков А. В. Математические олимпиады в школе. 5-11класс. – М.: Айрис-пресс, 2005.
Петерсон Л. Г. Математика. 5класс. – М.:Ювента, 2009.