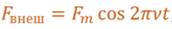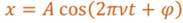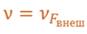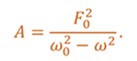Амплитуда резонансных явлений тем больше чем больше

Вынужденные колебания. Резонанс

Урок 40. Подготовка к ЕГЭ по физике. Часть 1. Механика.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Вынужденные колебания. Резонанс»

Данная тема посвящена вынужденным колебаниям и резонансу.

Ранее говорилось о колебательном движении и гармонических колебаниях. Гармоническими называются колебания, при которых смещение колеблющейся материальной точки происходит по закону синуса или косинуса.

Известно, что реальные колебания не происходят в точности по гармоническому закону. Ни один колебательный процесс в природе и технике не продолжается бесконечно долго, а имеет начало и конец во времени. А колебательный процесс, ограниченный во времени, не является гармоническим.

Но в природе встречаются колебательные процессы, протекающие весьма длительное время. Примером колебаний такого рода могут служить периодические изменения напряжения между различными участками человеческого тела, возникающие в результате работы сердца. График зависимости «вырабатываемого» сердечной мышцей напряжения от времени называется электрокардиограммой. Как видно из рисунка, она очень мало похожа на синусоиду. То есть колебания биотоков являются негармоническими.

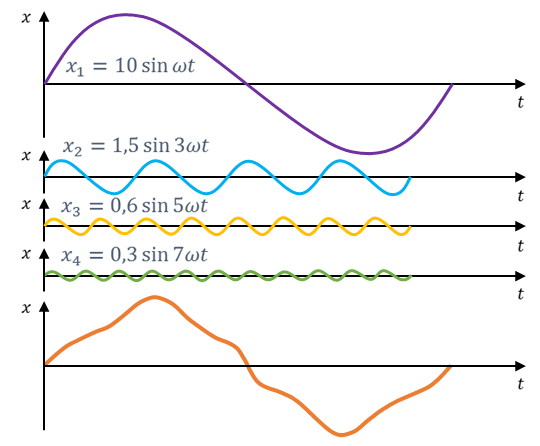
Однако, как показывают теоретические расчеты, любое периодическое колебание может быть математически представлено как сумма гармонических колебаний кратных частот, причем амплитуды гармоник этого ряда (ряда Фурье) с увеличением номера уменьшаются.

Также ранее рассматривались математический и пружинный маятники, колебания которых принимались за гармонические. Однако на самом деле, колебания маятников лишь близки к гармоническим, но не являются таковыми, так как тоже сопротивление воздуха и необратимые потери энергии на нагревание нити и пружины при их деформации приводят к тому, что амплитуда колебаний с течением времени уменьшается.

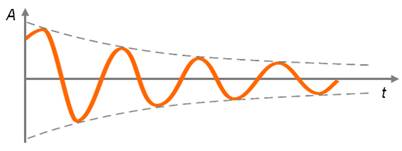
Колебания, амплитуда которых с течением времени уменьшается, называются затухающими.

Так как свободные колебания всегда затухают за то или иное время, то они не находят практического применения. Наиболее простой способ возбуждения незатухающих колебаний состоит в том, чтобы действовать на колебательную систему внешней периодической силой, возбуждающей колебания, которые сама система не совершала бы.

Работа этой внешней силы над системой обеспечивает приток энергии к ней извне, который не дает колебаниям затухать, несмотря на действие сил сопротивления.

Такие колебания, то есть колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями.

Основное отличие вынужденных колебаний от свободных состоит в том, что при свободных колебаниях система получает энергию только один раз, когда она выводится из положения равновесия, а при вынужденных колебаниях энергия постоянно пополняется за счет работы вынуждающей силы.

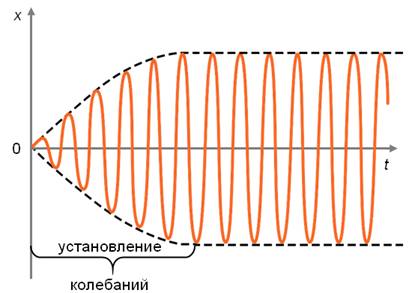
Вначале, в процессе установления вынужденных колебаний, они носят сложный характер: происходит наложение свободных затухающих, а также вынужденных колебаний. И только после того, как свободные колебания прекратятся, останутся только вынужденные колебания.

Рассмотрим некоторые особенности вынужденных колебаний.

1) Внешнее воздействие навязывает системе свой закон колебаний: так, если значение внешней силы изменяется по закону синуса (или косинуса), то вынужденные колебания будут являться гармоническими. Обратите внимание на то, что между вынужденными колебаниями и колебаниями внешней силы существует разность фаз.

где j – разность фаз.

2) Частота вынужденных колебаний равна частоте изменения вынуждающей силы.

3) Амплитуда вынужденных колебаний тем больше, чем больше амплитуда вынуждающей силы.

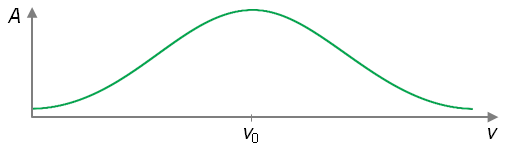
4) Амплитуда вынужденных колебаний зависит от частоты вынуждающего воздействия, она достигает максимального значения при совпадении частоты вынужденных колебаний с собственной частотой, то есть с частотой свободных колебаний системы. При частоте вынуждающей силы, приближающейся к собственной частоте колебаний системы, амплитуда колебаний растет, а при больших частотах — уменьшается.

Явление резкого возрастание амплитуды вынужденных колебаний, когда частота вынуждающей силы близка к частоте собственных колебаний системы, называется механическим резонансом.

Частота, при которой амплитуда вынужденных колебаний максимальна, называется резонансной.

А график зависимости амплитуды вынужденных колебаний от частоты называется резонансной кривой.

Явление резонанса имеет огромное практическое значение, так как используется для усиления различных колебаний в технике.

Например, вынужденные колебания используют при работе виброустройств для уплотнения сыпучего основания под фундаменты и дороги, уплотнения бетона при заливке фундаментов. Также вибраторы применяются дли вибрационного погружения свай и труб, при виброукладке бетона, сортировке сыпучих материалов.

Но механический резонанс может вызывать и разрушение колебательной системы, если амплитуда вынужденных колебаний превысит определенные пределы.

Поэтому, например, двигатель в автомобиле устанавливается на специальных амортизаторах, в которых механическая энергия колебаний гасится и переходит в тепловую.

В зданиях вибрирующие установки (такие, как электродвигатели, дизельные установки) размещают на резиновых или металлических амортизаторах. Иначе резкое возрастание амплитуды колебаний при резонансе может вызвать разрушение конструкций.

Резонансные явления возможны и в других сооружениях. Так, например, 16 апреля 1850 года близ города Анже во Франции на подвесном мосту Бас-Шен при движении по мосту батальона французских войск во время сильного ветра произошла первая «катастрофа-резонанса». Несмотря на отданную команду сбить шаг, солдаты непреднамеренно двигались синхронно в попытке сохранить равновесие на раскачивавшемся ветром мосту, что, вероятно, привело к увеличению амплитуды колебаний и дальнейшему обрушению моста. В результате обрушения погибло 226 человек.

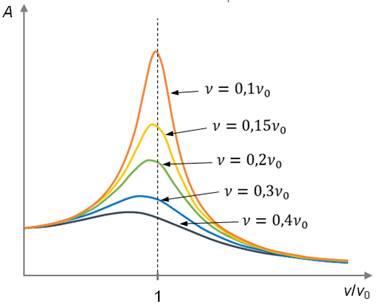
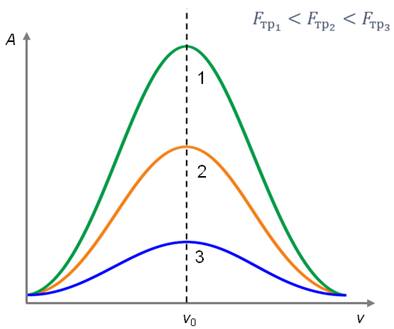
5) Амплитуда зависит от силы трения. Она уменьшается с увеличением силы трения, а резонансные кривые становятся более пологими (говорят, что наблюдается острый или тупой резонанс).

Если сила трения очень мала, то амплитуда вынужденных колебаний, как показывают расчеты, прямо пропорциональна квадрату амплитуды внешней периодической силы, и обратно пропорциональна разности квадратов циклических частот свободных и вынужденных колебаний системы.

Из формулы видно, что при стремлении частоты вынужденных колебаний к частоте свободных, амплитуда вынужденных колебаний стремится к бесконечности.

Среди различного рода колебательных движений можно также выделить и автоколебания. Автоколебаниями называются незатухающие колебания в системе, поддерживаемые внутренними источниками энергии при отсутствии воздействия внешней переменной силы.

Впервые термин автоколебания в русскоязычную терминологию был введен советским физиком Александром Александровичем Андроновым в 1928 году.

Примерами автоколебательных систем могут служить электрические звонки, двигатели внутреннего сгорания, часы с гирями и так далее.

Общее между автоколебаниями и свободными колебаниями в том, что их частота и амплитуда определяются свойствами самой колебательной системы.

А отличие автоколебаний от свободных затухающих колебаний в том, что их амплитуда не зависит от времени и от начального кратковременного воздействия, возбуждающего колебательный процесс.

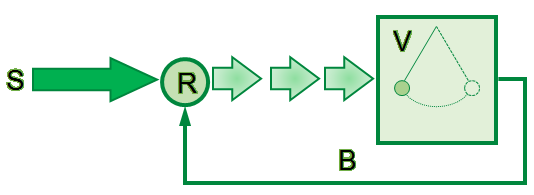
Как правило, автоколебательная система состоит из трех основных частей: колебательной системы V; источника энергии S; и устройства обратной связи B, регулирующего поступление энергии от источника к колебательной системе R.

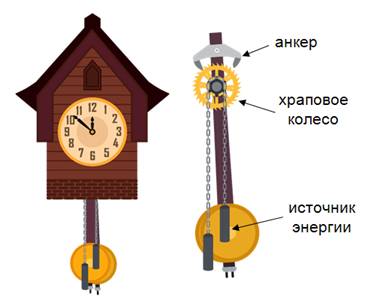
Простейшей механической автоколебательной системой являются маятниковые часы с гирями. В этих часах колебательная система — это маятник; источник энергии — это потенциальная энергия поднятой гири; а устройство обратной связи — это храповjе колесо и анкер. Потери механической энергии на трение при движении восполняются за счет уменьшения потенциальной энергии, спускающейся при каждом колебании маятника часов гири.

Вспомнили, какие колебания называются вынужденными. Рассмотрели особенности вынужденных колебаний. Вспомнили о явлении механического резонанса. А также поговорили об автоколебаниях и автоколебательных системах.

Источник

Вынужденные колебания. Резонанс. Резонансные кривые

Вынужденные колебания. Резонанс.

До сих пор мы рассматривали собственные колебания, колебания, происходящие в отсутствие внешних воздействий. Внешнее воздействие было нужно лишь для того, чтобы вывести систему из состояния равновесия, после чего она предоставлялась самой себе. Дифференциальное уравнение собственных колебаний вообще не содержит следов внешнего воздействия на систему: это воздействие отражается лишь в начальных условиях.

Установление колебаний.

Но очень часто приходится сталкиваться с колебаниями, которые происходят при постоянно присутствующем внешнем воздействии. Особенно важен и в то же время достаточно прост для изучения случай, когда внешняя сила имеет периодический характер. Общей чертой вынужденных колебаний, происходящих под действием периодической внешней силы, является то, что спустя некоторое время после начала действия внешней силы система полностью «забывает» свое начальное состояние, колебания приобретают стационарный характер и не зависят от начальных условий. Начальные условия проявляются только в период установления колебаний, который обычно называют переходным процессом.

Синусоидальное воздействие.

Рассмотрим вначале наиболее простой случай вынужденных колебаний осциллятора под действием внешней силы, изменяющейся по синусоидальному закону.

Такое внешнее воздействие на систему можно осуществить различными способами. Например, можно взять маятник в виде шарика на длинном стержне и длинную пружину с малой жесткостью и прикрепить ее к стержню маятника недалеко от точки подвеса, как показано на рис. 178.

Другой конец горизонтально расположенной пружины следует заставить двигаться по закону В с помошью кривошипно-шатунного механизма, приводимого в движение электромотором. Действующая на маятник со стороны пружины вынуждающая сила будет практически синусоидальна, если размах движения левого конца пружины В будет много больше амплитуды колебаний стержня маятника в точке закрепления пружины.

Уравнение движения.

Уравнение движения для этой и других подобных систем, в которых наряду с возвращающей силой и силой сопротивления на осциллятор действует вынуждающая внешняя сила, синусоидально изменяющаяся со временем, можно записать в видеЗдесь левая часть в соответствии со вторым законом Ньютона, является произведением массы на ускорение. Первый член в правой части представляет собой возвращающую силу, пропорциональную смещению из положения равновесия.

Для подвешенного на пружине груза это упругая сила, а во всех других случаях, когда ее физическая природа иная, эту силу называют квазиупругой. Второе слагаемое есть сила трения, пропорциональная скорости, например сила сопротивления воздуха или сила трения в оси. Амплитуду и частоту со раскачивающей систему вынуждающей силы будем считать постоянными.Разделим обе части уравнения на массу и введем обозначенияВ отсутствие вынуждающей силы правая часть уравнения обращается в нуль и оно, как и следовало ожидать, сводится к уравнению собственных затухающих колебаний.

Опыт показывает, что во всех системах под действием синусоидальной внешней силы в конце концов устанавливаются колебания, которые также происходят по синусоидальному закону с частотой вынуждающей силы со и с постоянной амплитудой а, но с некоторым сдвигом по фазе относительно вынуждающей силы. Такие колебания называются установившимися вынужденными колебаниями.Установившиеся колебания. Рассмотрим вначале именно установившиеся вынужденные колебания, причем для простоты пренебрежем трением. В этом случае в уравнении не будет члена, содержащего скорость.

Попробуем искать решение, соответствующее установившимся вынужденным колебаниям, в видеВычислим вторую производную и подставим ее вместе в уравнениеЧтобы это равенство было справедливо в любой момент времени, коэффициенты при слева и справа должны быть одинаковы. Из этого условия находим амплитуду колебаний. Исследуем зависимость амплитуды а от частоты со вынуждающей силы. График этой зависимости показан на рис. 179. Подставив сюда значения, видим, что постоянная во времени сила просто смещает осциллятор в новое положение равновесия, сдвинутое от старого.

Из следует, что при смещениеФазовые соотношения.

Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет немонотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении частоты со вынуждающей силы к собственной частоте со0 осциллятора называется резонансом.Формула дает выражение для амплитуды вынужденных колебаний в пренебрежении трением. Именно с этим пренебрежением связано обращение амплитуды колебаний в бесконечность при точном совпадении частот.

Реально амплитуда колебаний в бесконечность, конечно же, обращаться не может.Это означает, что при описании вынужденных колебаний вблизи резонанса учет трения принципиально необходим. При учете трения амплитуда вынужденных колебаний при резонансе получается конечной. Она будет тем меньше, чем больше трение в системе. Вдали от резонанса формулой можно пользоваться для нахождения амплитуды колебаний и при наличии трения, если оно не слишком сильное. Более того, эта формула, полученная без учета трения, имеет физический смысл только тогда, когда трение все же есть. Дело в том, что само понятие установившихся вынужденных колебаний применимо только к системам, в которых есть трение.

Если бы трения совсем не было, то процесс установления колебаний продолжался бы бесконечно долго. Реально это означает, что полученное без учета трения выражение для амплитуды вынужденных колебаний будет правильно описывать колебания в системе только спустя достаточно большой промежуток времени после начала действия вынуждающей силы. Слова «достаточно большой промежуток времени» означают здесь, что уже закончился переходный процесс, длительность которого совпадает с характерным временем затухания собственных колебаний в системе.

При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при со и в противофазе при, как и в отсутствие трения. Однако вблизи резонанса фаза меняется не скачком, а непрерывно, причем при точном совпадении частот смещение отстает по фазе от вынуждающей силы на (на четверть периода). Скорость изменяется при этом в фазе с вынуждающей силой, что обеспечивает наиболее благоприятные условия для передачи энергии от источника внешней вынуждающей силы к осциллятору.

• Какой физический смысл имеет каждый из членов в уравнении, описывающем вынужденные колебания осциллятора?

• Что такое установившиеся вынужденные колебания?

• При каких условиях можно использовать формулу для амплитуды установившихся вынужденных колебаний, полученную без учета трения?

• Что такое резонанс? Приведите известные вам примеры проявления и использования явления резонанса.

• Опишите сдвиг по фазе между вынуждающей силой и смешением при разных соотношениях между частотой в вынуждающей силы и собственной частотой осциллятора.

• Чем определяется длительность процесса установления вынужденных колебаний? Дайте обоснование ответа.

По этой ссылке вы найдёте полный курс лекций по математике:

Векторные диаграммы.

Убедиться в справедливости приведенных выше утверждений можно, если получить решение уравнения, описывающее установившиеся вынужденные колебания при наличии трения. Поскольку установившиеся колебания происходят с частотой вынуждающей силы со и некоторым сдвигом по фазе, то решение уравнения, соответствующее таким колебаниям, следует искать в видеПри этом скорость и ускорение, очевидно, тоже будут изменяться со временем по гармоническому закону.Амплитуду а установившихся вынужденных колебаний и сдвиг фазы удобно определять с помощью векторных диаграмм.

Воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по гармоническому закону величины можно представить как проекцию вектора на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с частотой со, а его неизменная длина равна амплитудному значению этой осциллирующей величины. В соответствии с этим сопоставим каждому члену уравнения вращающийся с угловой скоростью вектор, длина которого равна амплитудному значению этого члена.

Применяя теорему Пифагора, получаем откуда находим амплитуду установившихся вынужденных колебаний.Сдвиг фазы между вынуждающей силой и смещением, как видно из векторной диаграммы на рис. 182, отрицателен, так как вектор длины отстает от вектора. ПоэтомуИтак, установившиеся вынужденные колебания происходят по гармоническому закону, где определяются формулами.

Резонансные кривые.

Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Исследуем зависимость амплитуды колебаний от частоты со вынуждающей силы. При малом затухании у эта зависимость имеет очень резкий характер. Если, то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом.

При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Резонансные кривые при разных значениях постоянной затухания у приведены на рис. 183.

из положения равновесия под действием постоянной силы.Максимальная амплитуда. Амплитуду вынужденных колебаний в резонансе находим, подставляя частоту из в выражение.Амплитуда колебаний в резонансе тем больше, чем меньше постоянная затухания. При изучении вынужденных колебаний вблизи резонанса трением пренебрегать нельзя, как бы мало оно ни было: только при учете затухания амплитуда в резонансе яре, получается конечной.Интересно сравнить значение со статическим смещением под действием силы.

Составляя отношение, получаем при малом затуханииПодставляя сюда и учитывая, что есть время жизни собственных затухающих колебаний для той же системы в отсутствие внешних сил, находимНо есть число колебаний, совершаемых затухающим осциллятором за время жизни колебаний. Таким образом, резонансные свойства системы характеризуются тем же параметром, что и собственные затухающие колебания.Фазовые соотношения. Формула дает возможность проанализировать изменение сдвига фазы между внешней силой и смещением, при вынужденных колебаниях.

Возможно вам будут полезны данные страницы:

При значение д близко к нулю. Это означает, что при низких частотах смещение осциллятора происходит в фазе с внешней силой. При медленном вращении кривошипа на рис. 178 маятник движется в такт с правым концом шатуна.Если стремится к нулю со стороны отрицательных значений,сдвиг фазы равен и смещение осциллятора происходит в противофазе с вынуждающей силой. В резонансе, как видно из, смещение отстает по фазе от внешней силы.

Вторая из формул показывает, что при этом внешняя сила изменяется в фазе со скоростью все время действует в направлении движения. Что именно так и должно быть, ясно из интуитивных соображений.Резонанс скорости. Из формулы видно, что амплитуда колебаний скорости при установившихся вынужденных колебаниях равна. С помощью получаемЗависимость амплитуды скорости от частоты внешней силы показана на рис. 184.

Резонансная кривая для скорости хотя и похожа на резонансную кривую для смещения, но отличается от нее в некоторых отношениях. Так, при при действии постоянной силы, осциллятор испытывает статическое смещение из положенияравновесия и скорость его после того, как закончится переходный процесс, равна нулю. Из формулы видно, что амплитуда скорости при обращается в нуль. Резонанс скорости имеет место при точном совпадении частоты внешней силы с частотой свободных колебаний.

Рис. 184. Амплитуда скорости при установившихся вынужденных колебаниях

• Как строятся векторные диаграммы для установившихся вынужденных колебаний при синусоидальном внешнем воздействии?

• Чем определяется частота, амплитуда и фаза установившихся вынужденных гармонических колебаний?

• Опишите различия резонансных кривых для амплитуды смещения и амплитуды скорости. Какими характеристиками колебательной системы определяется острота резонансных кривых?

• Как связан характер резонансной кривой с параметрами системы, определяющими затухание ее собственных колебаний?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник