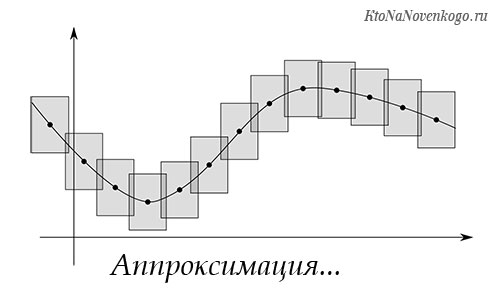
Аппроксимация пробега что это значит

Значение слова «аппроксимация»

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.

В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

аппроксима́ция

1. матем. приближённое выражение некоторых величин или объектов через другие, более простые величины или объекты ◆ Вследствие того, что массы элементарных частиц распределены в пределах многих порядков, аппроксимацию распределения целесообразно представить в логарифмическом масштабе. Воспоминания о Шкловском, «1996» (цитата из НКРЯ) ◆ Коэффициент аппроксимации 6,8% свидетельствует о высокой степени согласия уравнения регрессии с фактическими величинами. «Прогноз необходимости борьбы с непарным шелкопрядом в нагорных дубравах», 2004 г. // «Лесное хозяйство» (цитата из НКРЯ)

2. перен. филос. метод приближения, указание на приблизительный, неокончательный характер чего-либо

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова вазон (существительное):

Источник

Что такое аппроксимация

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.

Сегодня рассмотрим один из них, термин «аппроксимация».

Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.

Аппроксимация в математике — это …

Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».

Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).

Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.

Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.

Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.

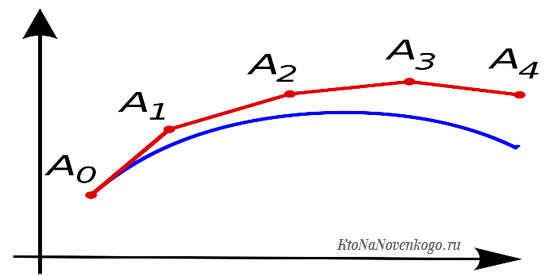
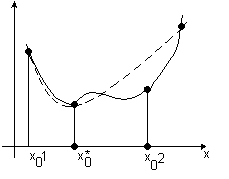
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:

Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.

Термин «аппроксимация» схож по сути со следующими математическими понятиями:

Применение термина «аппроксимация» в иных областях

Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.

Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).

Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.

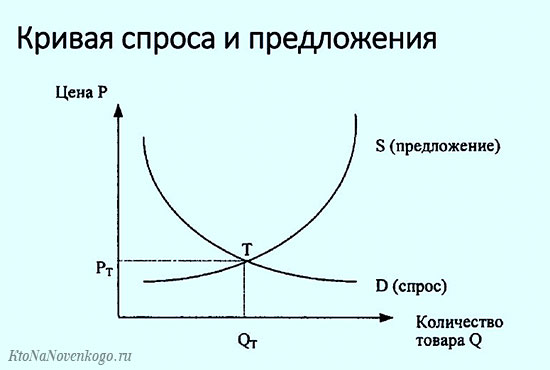
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:

На самом деле на спрос и предложение влияние оказывают и другие факторы.

При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.

Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».

Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.

Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.

Краткое резюме

Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.

Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.

Читайте наш блог, это познавательно!

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?

Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.

Источник

Аппроксимация в Excel

(Обратите внимание на дополнительный раздел от 04.06.2017 в конце статьи.)

Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.

Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.

Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.

«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…

«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…

«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…

«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…

Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда. ». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.

В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.

Аппроксимация в Excel статистических данных аналитической функцией.

Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.

Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.

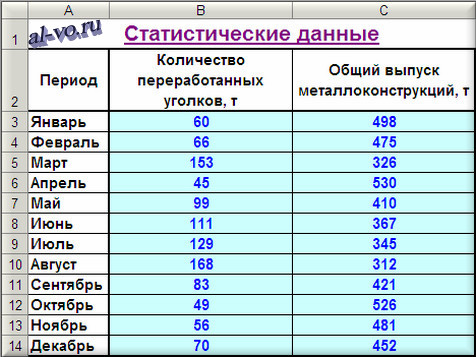
1. Включаем Excel и помещаем на лист таблицу с данными статистики.

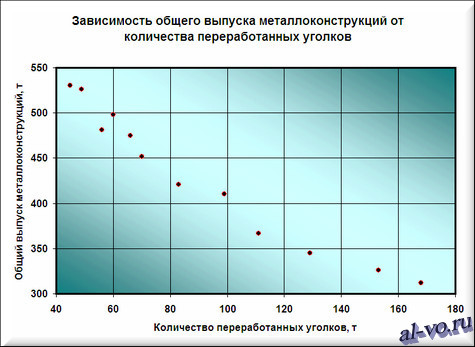
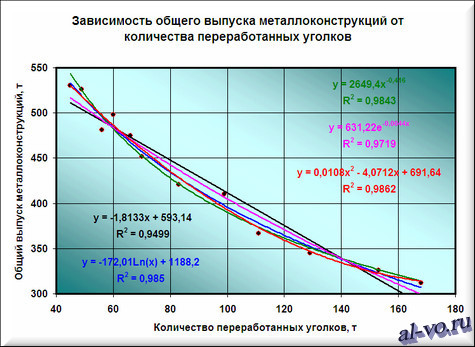
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.

О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».

3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».

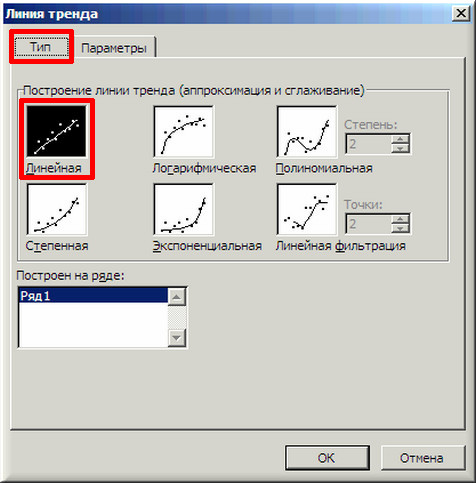
4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».

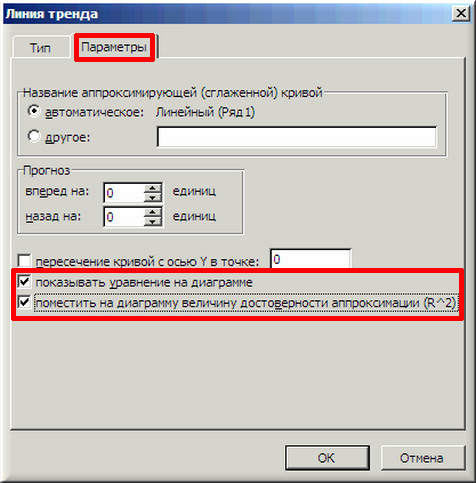
5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».

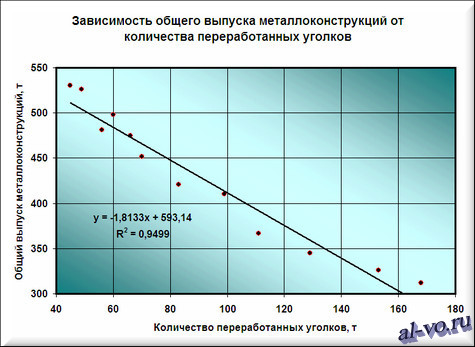
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.

Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R 2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!

7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.

Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…. Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл. Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!

Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.

8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».

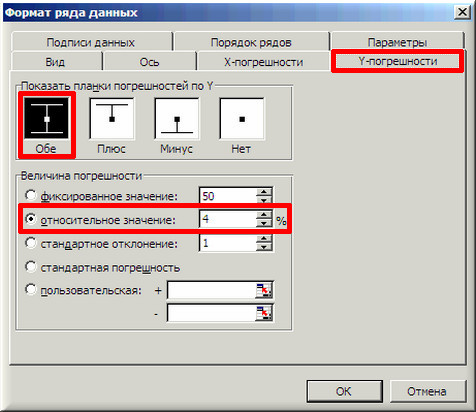
9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.

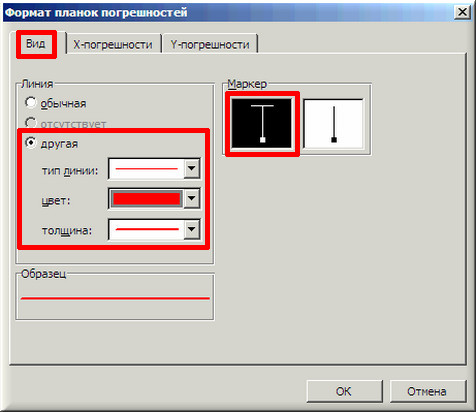
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.

Аналогичным образом форматируются любые другие объекты диаграммы в Excel!

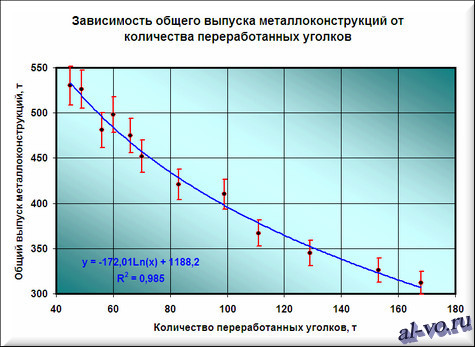
Окончательный результат диаграммы представлен на следующем снимке экрана.

Итоги.

Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.

Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.

Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R 2 >0,87. Отличный результат – при R 2 >0,94.

На практике бывает трудно выделить один самый главный определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!

В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.

Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.

Подписывайтесь на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы.

Не забывайте подтверждать подписку кликом по ссылке в письме, которое придет к вам на указанную почту (может прийти в папку «Спам»).

С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!

P.S. (04.06.2017)

Высокоточная красивая замена табличных данных простым уравнением.

Вас не устраивают полученные точность аппроксимации (R 2 2 =0,9963.

Источник

Аппроксимация

Добавлено в закладки: 0

Что такое аппроксимация – это научный метод, который можно использовать в разных областях познания. В дословном переводе он означает «приближение», и под ним подразумевается замена одних объектов, которые изучаются, на другие, схожие с исходными и более простые.

Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.

Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.

Рассмотрим, более детально, ч то значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.

Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.

В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

Остаточный член

Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.

Примеры

Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.

Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.

Мы надеемся, что да ли наиболее полное определение и понятие термина аппроксимация, привели ее примеры

Источник

Аппроксимированная синусоида – что это и как с ней бороться

Отправим материал на почту

Для чего нам нужна аппроксимированная синусоида и что она может дать? Какими бы надежными ни были линии электропередач, снабжающие нас энергией от ГРЭС (КЭС), АЭС и ТЭС, всегда может случиться авария или рядовая поломка, что приведет к обесточиванию жилья и/или предприятия, организации, учреждения. И вот здесь зачастую потребитель переключается на автономные источники питания – ИБП или генератор (если они есть).

На первый взгляд все просто: при отключении света автоматически или вручную запускается какой-то дизельный или другой генератор и подача электроэнергии возобновляется, но это не совсем так. Загвоздка в том, что не все инверторы способны выдавать синусоидальное переменное напряжение, необходимое для бытового и промышленного оборудования. Конечно, в любом случае оно будет переменным, но без чистой синусоидальной формы. Если еще проще, то источник бесперебойного питания, предназначенный для лампы накаливания, не подойдёт для любого котла отопления.

О синусоиде

Давайте разберемся, чем чистая синусоида отличается от аппроксимированной, и для этого посмотрите на изображение вверху. Вы видите, что у чистого синуса линия ровная, без каких-либо сдвигов. Это очень важно, потому что большинство электродвигателей, индукционных катушек, дросселей и т.п. могут работать только в том случае, если форма выходного напряжения имеет чистый, гладкий синус. Конечно, идеально ровным он не может быть и на деле коэффициент гармонии должен быть менее 8%, но об этом чуть ниже.

Если на каком-либо ИБП или генераторе вы видите английский текст «Total Harmonic Distortion», а после него число с процентами, значит, вы столкнулись с добросовестным производителем. Дело в том, что приборы с аппроксимацией синусоиды зачастую продаются без информации об этом факте, так как такое устройство проще продать неосведомленному покупателю. А вот на устройствах или их документах с чистой синусоидой обязательно будет подтверждение, что это так и есть.

Видео описание

Обман от производителей инверторов.

Вот какими могут быть коэффициенты по отклонениям (обозначаются в процентах):

Источников бесперебойного питания существует немало – их производят почти во всех странах мира, но, по большому счету все приборы можно классифицировать только по трем типам:

В сопроводительных документах или на наружной маркировке (на корпусе) резервных ИБП (1) можно встретить обозначение «Back», но если оно двойное и выглядит, как «Back-UPS», то о гладкой синусоиде можно забыть. Здесь технические параметры полностью зависимы от инвертора, а в недорогих моделях такого типа встроенного преобразователя попросту не может быть. Если инвертор все-таки есть, то стоимость прибора значительно возрастет.

Когда вы выбираете линейно-активный источник бесперебойного питания line-interactive (2), то возможность купить прибор с преобразователем на чистый синус значительно увеличивается. По визуальным признакам наличие такого инвертора можно определить, если в документах или на наружной маркировке (на корпусе) увидите обозначение «Smart», но это только предположение, так как «Back-UPS» тоже стали порой использовать эти символы. Более точно вы сможете узнать у продавца или при тщательном изучении технических характеристик от завода-изготовителя.

И, наконец, модели on-line (3), в которых обязательно есть двойной инвертор на чистую синусоиду. Неоспоримое преимущество такого прибора в том, что он работает на выравнивание аппроксимированной синусоиды не только во время отключения ЛЭП (от аккумуляторов), но и в обычном режиме. Главный недостаток on-line модификаций, это их высокая цена.

Примечание: ИБП с двойным преобразователем позволяют производить подключение внешнего питания, что в значительной степени увеличивает автономный ресурс агрегата.

Видео описание

Как проверить форму напряжения ИБП без осцилографа.

Варианты применения ИБП с аппроксимированной синусоидой

Как вы уже поняли, можно допускать применение инверторов ИБП: синусоидальная аппроксимация присутствует и с чистой синусоидой. Все зависит от оборудования, которое будет получать электроэнергию через такие источники.

Где ступенчатая синусоида не мешает

Если оборудование не имеет в своей схеме диммеров (электронных приборов регулировки), конденсаторов, индуктивных катушек и использует активную нагрузку, то оно не восприимчиво к той или иной синусоиде. Таких приборов не очень много, но они все-таки есть, и мы их широко используем в быту:

Негативное влияние аппроксимации

В Сети иногда проскакивает мнение, что все осветительные приборы могут функционировать от ИБП с аппроксимированной синусоидой, но это только полуправда. В большинстве случаев мы не используем не «лампочку Ильича», а более современные светильники с преобразователем напряжения ≈220-230 V. Подавляющее большинство людей даже не задумываются над принципами работы таких осветительных приборов, но посмотрите результаты теста некоторых из них, которые представлены в таблице ниже.

В таблице сравниваются параметры разных моделей светильников при подключении к обычной сети ≈220-230 V и к источнику бесперебойного питания, где присутствует ступенчатая аппроксимация синусоиды. Для эксперимента был использован ИБП компании APC с мощностью 500 V*A.

Даже неискушенный пользователь заметит, что электрические характеристики приборов освещения становятся другими при модифицированной синусоиде и эти изменения происходят с негативом – потребляемый ток возрастает, а КПД (яркость) падает. Возможна также ещё одна реакция, например, когда для ограничения мощности добавляют конденсатор, он соберет все реактивные токи, что одновременно будут делать диоды, и мощность, конечно же, увеличится в несколько раз, но это очень быстро выведет лампу из строя. Но при подключении к другому автономному ИБП 12/220 V такой картины не наблюдается, и лампа работает нормально.

Отсюда можно сделать вывод: подключение светодиодов или люминесцентных ламп на квази-синус зависит от случая: может сгореть, но может функционировать в нормальном режиме. Если говорить о правильной работе приборов, где в значительной степени присутствуют реактивные токи, а также для устройств, которые чувствительны к помехам, то придется использовать только источники типа on-line, выдающих чистую синусоиду.

Среди агрегатов, которым в любом случае противопоказана аппроксимированная синусоида можно назвать:

Видео описание

Чистый и модифицированный синус. В чем отличие.

Заключение

Подводя итоги можно сказать, что использование ступенчатой синусоиды для приборов, генерирующих реактивные токи, в лучшем случае обернется невозможностью их запуска, а худшие варианты – это падение коэффициента мощности и даже быстрый выход из строя. Потому источники бесперебойного питания типа on-line, где на выходе чистый синус, это лучший вариант бесперебойника как на промышленном, так и на бытовом уровне.

Источник