Аппроксимировать это что значит
Значение слова «аппроксимация»
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
аппроксима́ция
1. матем. приближённое выражение некоторых величин или объектов через другие, более простые величины или объекты ◆ Вследствие того, что массы элементарных частиц распределены в пределах многих порядков, аппроксимацию распределения целесообразно представить в логарифмическом масштабе. Воспоминания о Шкловском, «1996» (цитата из НКРЯ) ◆ Коэффициент аппроксимации 6,8% свидетельствует о высокой степени согласия уравнения регрессии с фактическими величинами. «Прогноз необходимости борьбы с непарным шелкопрядом в нагорных дубравах», 2004 г. // «Лесное хозяйство» (цитата из НКРЯ)
2. перен. филос. метод приближения, указание на приблизительный, неокончательный характер чего-либо
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова бинтовой (прилагательное):
Что такое аппроксимация
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.
Сегодня рассмотрим один из них, термин «аппроксимация».
Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.
Аппроксимация в математике — это …
Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».
Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).
Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.
Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.
Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.
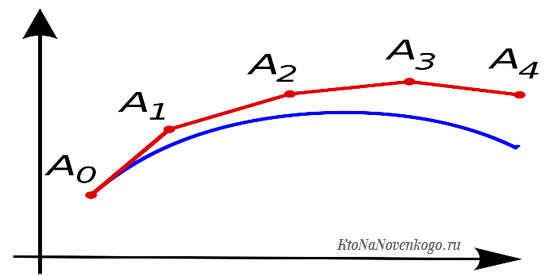
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:
Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.
Термин «аппроксимация» схож по сути со следующими математическими понятиями:
Применение термина «аппроксимация» в иных областях
Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.
Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).
Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.
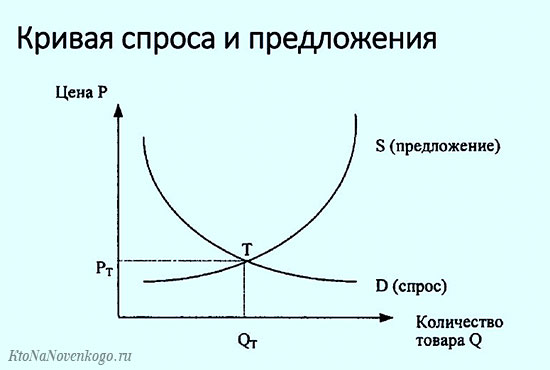
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:
На самом деле на спрос и предложение влияние оказывают и другие факторы.
При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.
Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».
Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.
Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.
Краткое резюме
Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.
Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.
Читайте наш блог, это познавательно!
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?
Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.
Аппроксимация
Добавлено в закладки: 0
Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.
Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.
Рассмотрим, более детально, ч то значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.
Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.
В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
Остаточный член
Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.
Примеры
Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:
Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.
Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.
Мы надеемся, что да ли наиболее полное определение и понятие термина аппроксимация, привели ее примеры