Авл что это такое
Авл что это такое
Смотреть что такое «АВЛ» в других словарях:
АВЛ — армейский ветеринарный лазарет воен., мед. Словари: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с., Новый словарь сокращений русского языка, М.: ЭТС, 1995. АВЛ АК АВЛ авиакомпания «Архангельские… … Словарь сокращений и аббревиатур
қавл — I [قول] а 1. гуфтор, сухан, калом; аз қавли… аз гапи…, аз сухани…; аз рӯи қавли… // назар ба қавли… мувофиқи гапи…, тибқи гуфтаи…; ба қавли… бино ба гуфтаи…, ба гуфти…, аз рӯи гапи… тавре ки мегӯя(н)д 2. фикр, ақида 3. аҳд, паймон, мисоқ; ваъда;… … Фарҳанги тафсирии забони тоҷикӣ
АВЛ — Эта страница ранее удалялась или была переименована (что это значит?) 22:54, 27 декабря 2012 CodeMonk (обсуждение | вклад) удалил страницу АВЛ (О7: для возможности переименования: <
авл — I [عول] а. кит. майл, тамоюл II [عول] а. кит. нигаҳдории аёл, таъмини оила … Фарҳанги тафсирии забони тоҷикӣ
ҳавл — [هول] хавф, тарс, бим, ваҳшат; ҳавлу ҳарос тарсу бим … Фарҳанги тафсирии забони тоҷикӣ
ҳавлӣ — [حولي] иқоматгоҳи гирдогирдаш девор кашидаи саҳндори иборат аз чанд хона … Фарҳанги тафсирии забони тоҷикӣ
Авл Корнелий Косс — лат. Aulus Cornelius Cossus Военный трибун 437 до н. э. или 426 до н. э., консул 428 до н. э., великий понтифик ок. 431 420 до н. э … Википедия
Авл Лициний Нерва Силиан — лат. Aulus Licinius Nerva Silianus Консул Римской империи … Википедия
Авл Клавдий Харакс — лат. Aulus Claudius Charax Консул суффект Римской империи … Википедия
Авл Цецилий Фаустин — лат. Aulus Caecilius Faustinus Консул суффект Римской империи … Википедия
Авл что это такое
армейский ветеринарный лазарет
Словари: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с., Новый словарь сокращений русского языка, М.: ЭТС, 1995.
авиакомпания «Архангельские воздушные линии»
авиа, г. Архангельск, организация
автоматическое выключение лазера
Словари: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. — М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2003. — 318 с., С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с., Новый словарь сокращений русского языка, М.: ЭТС, 1995.
автомат выбора линии
Полезное
Смотреть что такое «АВЛ» в других словарях:
қавл — I [قول] а 1. гуфтор, сухан, калом; аз қавли… аз гапи…, аз сухани…; аз рӯи қавли… // назар ба қавли… мувофиқи гапи…, тибқи гуфтаи…; ба қавли… бино ба гуфтаи…, ба гуфти…, аз рӯи гапи… тавре ки мегӯя(н)д 2. фикр, ақида 3. аҳд, паймон, мисоқ; ваъда;… … Фарҳанги тафсирии забони тоҷикӣ
АВЛ — Эта страница ранее удалялась или была переименована (что это значит?) 22:54, 27 декабря 2012 CodeMonk (обсуждение | вклад) удалил страницу АВЛ (О7: для возможности переименования: <
АВЛ — авианосец лёгкий армейский ветеринарный лазарет … Словарь сокращений русского языка
авл — I [عول] а. кит. майл, тамоюл II [عول] а. кит. нигаҳдории аёл, таъмини оила … Фарҳанги тафсирии забони тоҷикӣ
ҳавл — [هول] хавф, тарс, бим, ваҳшат; ҳавлу ҳарос тарсу бим … Фарҳанги тафсирии забони тоҷикӣ
ҳавлӣ — [حولي] иқоматгоҳи гирдогирдаш девор кашидаи саҳндори иборат аз чанд хона … Фарҳанги тафсирии забони тоҷикӣ
Авл Корнелий Косс — лат. Aulus Cornelius Cossus Военный трибун 437 до н. э. или 426 до н. э., консул 428 до н. э., великий понтифик ок. 431 420 до н. э … Википедия
Авл Лициний Нерва Силиан — лат. Aulus Licinius Nerva Silianus Консул Римской империи … Википедия
Авл Клавдий Харакс — лат. Aulus Claudius Charax Консул суффект Римской империи … Википедия
Авл Цецилий Фаустин — лат. Aulus Caecilius Faustinus Консул суффект Римской империи … Википедия
Авальный кредит
Финансовый эксперт с высшим экономическим образованием по специальности «Экономист-менеджер». Имею опыт работы в Сбербанке России. Более 7 лет консультирую читателей по финансовым вопросам.
Все эти нюансы прописаны в договоре, заключённом между банком и клиентом. Там же прописан перечень конкретных ситуаций, при которых данное условие вступает в силу.
Авальный кредит простыми словами
Авальный кредит является своеобразной формой поручительства или гарантией платёжеспособности клиента. Данная вариация займов может быть представлена краткосрочным или долгосрочным продуктом.
Авальный кредит является весьма распространённым явлением в рыночной экономике. Главная цель, преследуемая при этом — минимизирование риска в клиентской деятельности. Наиболее популярные формы, которые способен принимать данный банковский продукт — поручительство по кредиту, гарантия платежа, гарантия твёрдого предложения товара, предоставление ссуды. Также сюда можно отнести ещё и разные виды поручительства — налоговые, таможенные, судебные.
Особенности авального кредита
Обязательным составляющим данной финансовой операции является факт заключения договора между банковской организацией и потенциальным клиентом. В контракте прописываются все ситуации, при которых финансовое учреждение становится авалистом. Этого статуса оно лишается в момент, когда вексельные обязательства были полностью выполнены.
Существует стандартный набор документов, необходимых для заключения договора подобного типа. В случае отсутствия каких-либо бумаг продолжение сотрудничества не будет возможным. В названный список документов входят: заявление о выдаче вексельного поручительства, копии учредительных документов, оригиналы векселей, подтверждение товарного характера векселей в письменном виде, справка о состоянии собственного расчётного счёта. А при условии, если клиент сотрудничает с другой финансовой организацией, необходимо ещё предоставить и карточку с подписью.
После того, как необходимый пакет документов полностью собран, он отправляется на рассмотрение к сотрудникам банка, являющимся специалистами в данном вопросе. По истечении определённого промежутка времени выносится решение, которое может быть положительным или отрицательным для потенциального клиента учреждения.
Отказ в получении авального кредита
Существует целый ряд причин, по которым клиенту может быть отказано в выдаче такого банковского продукта. Одно из главных ограничений распространяется на юридических лиц, чьи векселя были опротестованы в период действующего календарного года.
Отказ может получить ещё одна категория клиентов, которые на момент подписания договора имеют просроченную задолженность по кредиту. В случае, если заёмщик имеет открытый счёт в другом финансовом учреждении, попытка сотрудничества также не увенчается для него успехом.
Детали сотрудничества
Банк, предоставляющий аваль, взимает дополнительную плату с клиента. Величина комиссии определяется уровнем финансового рынка риска — чем он будет выше, тем больше будет процент. Аваль предоставляется в общепринятой всем форме — с наличием печати и непосредственным написанием аваля. В случае необходимости клиенту может быть выдано гарантийное письмо, в котором указываются обязательства сторон и прописаны штрафные санкции, применимые к каждой из них и на каком основании.
АВЛ-деревья
Если в одном из моих прошлых постов речь шла о довольно современном подходе к построению сбалансированных деревьев поиска, то этот пост посвящен реализации АВЛ-деревьев — наверное, самого первого вида сбалансированных двоичных деревьев поиска, придуманных еще в 1962 году нашими (тогда советскими) учеными Адельсон-Вельским и Ландисом. В сети можно найти много реализаций АВЛ-деревьев (например, тут), но все, что лично я видел, не внушает особенного оптимизма, особенно, если пытаешься разобраться во всем с нуля. Везде утверждается, что АВЛ-деревья проще красно-черных деревьев, но глядя на прилагаемый к этому код, начинаешь сомневаться в данном утверждении. Собственно, желание объяснить на пальцах, как устроены АВЛ-деревья, и послужило мотивацией к написанию данного поста. Изложение иллюстрируется кодом на С++.
Понятие АВЛ-дерева
АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.
Особенностью АВЛ-дерева является то, что оно является сбалансированным в следующем смысле: для любого узла дерева высота его правого поддерева отличается от высоты левого поддерева не более чем на единицу. Доказано, что этого свойства достаточно для того, чтобы высота дерева логарифмически зависела от числа его узлов: высота h АВЛ-дерева с n ключами лежит в диапазоне от log2(n + 1) до 1.44 log2(n + 2) − 0.328. А так как основные операции над двоичными деревьями поиска (поиск, вставка и удаление узлов) линейно зависят от его высоты, то получаем гарантированную логарифмическую зависимость времени работы этих алгоритмов от числа ключей, хранимых в дереве. Напомним, что рандомизированные деревья поиска обеспечивают сбалансированность только в вероятностном смысле: вероятность получения сильно несбалансированного дерева при больших n хотя и является пренебрежимо малой, но остается не равной нулю.
Структура узлов
Будем представлять узлы АВЛ-дерева следующей структурой:
Поле key хранит ключ узла, поле height — высоту поддерева с корнем в данном узле, поля left и right — указатели на левое и правое поддеревья. Простой конструктор создает новый узел (высоты 1) с заданным ключом k.
Определим три вспомогательные функции, связанные с высотой. Первая является оберткой для поля height, она может работать и с нулевыми указателями (с пустыми деревьями):
Вторая вычисляет balance factor заданного узла (и работает только с ненулевыми указателями):
Третья функция восстанавливает корректное значение поля height заданного узла (при условии, что значения этого поля в правом и левом дочерних узлах являются корректными):
Заметим, что все три функции являются нерекурсивными, т.е. время их работы есть величина О(1).
Балансировка узлов
Код, реализующий правый поворот, выглядит следующим образом (как обычно, каждая функция, изменяющая дерево, возвращает новый корень полученного дерева):
Левый поворот является симметричной копией правого:
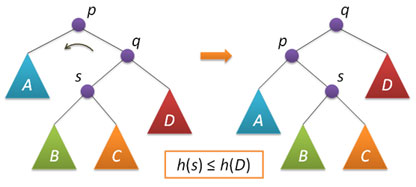
Рассмотрим теперь ситуацию дисбаланса, когда высота правого поддерева узла p на 2 больше высоты левого поддерева (обратный случай является симметричным и реализуется аналогично). Пусть q — правый дочерний узел узла p, а s — левый дочерний узел узла q.
Анализ возможных случаев в рамках данной ситуации показывает, что для исправления расбалансировки в узле p достаточно выполнить либо простой поворот влево вокруг p, либо так называемый большой поворот влево вокруг того же p. Простой поворот выполняется при условии, что высота левого поддерева узла q больше высоты его правого поддерева: h(s)≤h(D).
Большой поворот применяется при условии h(s)>h(D) и сводится в данном случае к двум простым — сначала правый поворот вокруг q и затем левый вокруг p.
Код, выполняющий балансировку, сводится к проверке условий и выполнению поворотов:
Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.
Вставка ключей
Вставка нового ключа в АВЛ-дерево выполняется, по большому счету, так же, как это делается в простых деревьях поиска: спускаемся вниз по дереву, выбирая правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. Единственное отличие заключается в том, что при возвращении из рекурсии (т.е. после того, как ключ вставлен либо в правое, либо в левое поддерево, и это дерево сбалансировано) выполняется балансировка текущего узла. Строго доказывается, что возникающий при такой вставке дисбаланс в любом узле по пути движения не превышает двух, а значит применение вышеописанной функции балансировки является корректным.
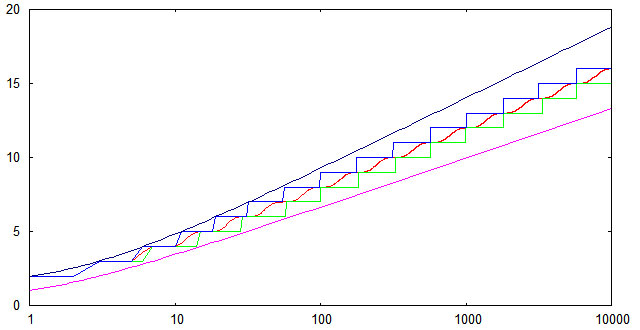
Чтобы проверить соответствие реализованного алгоритма вставки теоретическим оценкам для высоты АВЛ-деревьев, был проведен несложный вычислительный эксперимент. Генерировался массив из случайно расположенных чисел от 1 до 10000, далее эти числа последовательно вставлялись в изначально пустое АВЛ-дерево и измерялась высота дерева после каждой вставки. Полученные результаты были усреднены по 1000 расчетам. На следующем графике показана зависимость от n средней высоты (красная линия); минимальной высоты (зеленая линия); максимальной высоты (синяя линия). Кроме того, показаны верхняя и нижняя теоретические оценки.
Видно, что для случайных последовательностей ключей экспериментально найденные высоты попадают в теоретические границы даже с небольшим запасом. Нижняя граница достижима (по крайней мере в некоторых точках), если исходная последовательность ключей является упорядоченной по возрастанию.
Удаление ключей
С удалением узлов из АВЛ-дерева, к сожалению, все не так шоколадно, как с рандомизированными деревьями поиска. Способа, основанного на слиянии (join) двух деревьев, ни найти, ни придумать не удалось.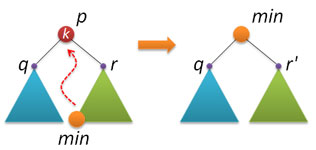 
Поэтому за основу был взят вариант, описываемый практически везде (и который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска). Идея следующая: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min.
При реализации возникает несколько нюансов. Прежде всего, если у найденный узел p не имеет правого поддерева, то по свойству АВЛ-дерева слева у этого узла может быть только один единственный дочерний узел (дерево высоты 1), либо узел p вообще лист. В обоих этих случаях надо просто удалить узел p и вернуть в качестве результата указатель на левый дочерний узел узла p.
Пусть теперь правое поддерево у p есть. Находим минимальный ключ в этом поддереве. По свойству двоичного дерева поиска этот ключ находится в конце левой ветки, начиная от корня дерева. Применяем рекурсивную функцию:
Еще одна служебная функция у нас будет заниматься удалением минимального элемента из заданного дерева. Опять же, по свойству АВЛ-дерева у минимального элемента справа либо подвешен единственный узел, либо там пусто. В обоих случаях надо просто вернуть указатель на правый узел и по пути назад (при возвращении из рекурсии) выполнить балансировку. Сам минимальный узел не удаляется, т.к. он нам еще пригодится.
Теперь все готово для реализации удаления ключа из АВЛ-дерева. Сначала находим нужный узел, выполняя те же действия, что и при вставке ключа:
Как только ключ k найден, переходим к плану Б: запоминаем корни q и r левого и правого поддеревьев узла p; удаляем узел p; если правое поддерево пустое, то возвращаем указатель на левое поддерево; если правое поддерево не пустое, то находим там минимальный элемент min, потом его извлекаем оттуда, слева к min подвешиваем q, справа — то, что получилось из r, возвращаем min после его балансировки.
При выходе из рекурсии не забываем выполнить балансировку:
Вот собственно и все! Поиск минимального узла и его извлечение, в принципе, можно реализовать в одной функции, при этом придется решать (не очень сложную) проблему с возвращением из функции пары указателей. Зато можно сэкономить на одном проходе по правому поддереву.
Очевидно, что операции вставки и удаления (а также более простая операция поиска) выполняются за время пропорциональное высоте дерева, т.к. в процессе выполнения этих операций производится спуск из корня к заданному узлу, и на каждом уровне выполняется некоторое фиксированное число действий. А в силу того, что АВЛ-дерево является сбалансированным, его высота зависит логарифмически от числа узлов. Таким образом, время выполнения всех трех базовых операций гарантированно логарифмически зависит от числа узлов дерева.
АВЛ-дерево.
АВЛ-дерево – структура данных, изобретенная в 1968 году двумя советскими математиками: Евгением Михайловичем Ландисом и Георгием Максимовичем Адельсон-Вельским. Прежде чем дать конструктивное определение АВЛ-дереву, сделаем это для сбалансированного двоичного дерева поиска.
Сбалансированным называется такое двоичное дерево поиска, в котором высота каждого из поддеревьев, имеющих общий корень, отличается не более чем на некоторую константу k, и при этом выполняются условия характерные для двоичного дерева поиска.
АВЛ-дерево – сбалансированное двоичное дерево поиска с k=1. Для его узлов определен коэффициент сбалансированности (balance factor). Balance factor – это разность высот правого и левого поддеревьев, принимающая одно значение из множества <-1, 0, 1>. Ниже изображен пример АВЛ-дерева, каждому узлу которого поставлен в соответствие его реальный коэффициент сбалансированности.
Пример АВЛ-дерева
Положим Bi – коэффициент сбалансированности узла Ti (i – номер узла, отсчитываемый сверху вниз от корневого узла по уровням слева направо). Balance factor узла Ti рассчитывается следующим образом. Пусть функция h() с параметрами Tiи L возвращает высоту левого поддерева L узла Ti, а с Ti и R – правого. Тогда Bi=h(Ti, R)-h(Ti, L). Например, B4=-1, так как h(T4, R)-h(T4, L)=0-1=-1.
Сбалансированное дерево эффективно в обработке, что следует из следующих рассуждений. Максимальное количество шагов, которое может потребоваться для обнаружения нужного узла, равно количеству уровней самого бинарного дерева поиска. А так как поддеревья сбалансированного дерева, «растущие» из произвольного корня, практически симметричны, то и его листья расположены на сравнительно невысоком уровне, т. е. высота дерева сводиться к оптимальному минимуму. Поэтому критерий баланса положительно сказывается на общей производительности. Но в процессе обработки АВЛ-дерева, балансировка может нарушиться, тогда потребуется осуществить операцию балансировки. Помимо нее, над АВЛ-деревом определены операции вставки и удаления элемента. Именно выполнение последних может привести к дисбалансу дерева.
Доказано, что высота АВЛ-дерева, имеющего N узлов, примерно равна log2N. Беря в виду это, а также то, то, что время выполнения операций добавления и удаления напрямую зависит от операции поиска, получим временную сложность трех операций для худшего и среднего случая – O(logN).
Прежде чем рассматривать основные операции над АВЛ-деревом, определим структуру для представления его узлов, а также три специальные функции: