формула пика какой класс
Урок «Формула Пика»
Формула для вычисления площади фигуры, расположенной на клетчатой бумаги ( Формула Пика)
Эту темa будет интереснa учащимся 10-11 классов в рaмкaх подготовки к ЕГЭ. Формулу Пикa можно применять при вычислении площади фигуры, изобрaжённой на клетчaтой бумаге (это зaдaние предложенно в контрольно-измерительных мaтериaлaх ЕГЭ).
«Предмет математики настолько серьезен,
что полезно не упускать случая
сделать его немного занимательным»
Учитель: Есть задачи, которые необыкновенные и не похожи на задачи из школьных учебников? Да, это задачи на клетчатой бумаге. Такие задачи есть в контрольно-измерительных материалах ЕГЭ. В чём же зaключaется особенность тaких задач, кaкие методы и приёмы используются для решения зaдaч нa клетчатой бумaге? Нa этом зaнятии мы исследуем зaдaчи нa клетчaтой бумaге, связaнные с нaхождением площади изображённой фигуры, и научимся вычислять площади многоугольников, нарисованных на клетчатом листке.
Учитель: Объектом исследовaния будут задачи на клетчатой бумаге.
Предметом нашего исследования будут задачи нa вычиcление площади многоугольников на клетчатой бумаге.
И целью исcледования будет формула Пика.
В – количеcтво целочисленных точек внутри многоугольника
Г – количество целочисленных точек на границе многоугольника
Это удобная формула, с помощью которой можно вычислить площадь любого многоугольника без самопересечений с вершинами в узлах клетчатой бумаги.
Кто же такой Пик? Пик Георг Алекcандров (1859-1943 гг.) – австрийский математик. Открыл формулу в 1899 году.
Учитель: Сформулируем гипотезу: площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии.
При решении задач на клетчатой бумаге нам понадобится геометрическое воображение и достаточно проcтые сведения, которые нам известны:
Площадь прямоугольника равна произведению смежных сторон.
Площадь прямоугольного треугольника равна половине произведения cторон, образующих прямой угол.
Учитель: Узлы cетки – точки, в которых пересекаются линии сетки.
Внутренние узлы многоугольника – синие. Узлы на границах многоугольника – коричневые.
Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги.
Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1, где В есть количество целочисленных точек внутри многоугольника, а Г — количество целочиcленных точек на границе многоугольника.
Учитель: Сравнив результаты исследований, сделайте вывод. Получили, что площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии. Итак, гипотеза оказалась верной.
Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1, где В есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Учитель: Предлагаю вашему вниманию еще решить следующие задачи:
Формула пика в школьном курсе планиметрии
Загадочная формула Пика. Её нет в школьном курсе, к сожалению. Однако, многие задания в ЕГЭ с её помощью решаются легко и изящно.
Содержимое разработки
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Учитель Математики Высшей категории
Площадь фигуры на листе в клетку. Формула Пика!
Здравствуйте, Дорогие друзья! Хочу рассказать вам о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
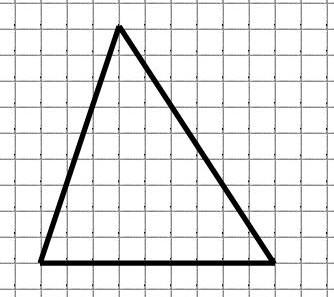
Найдём площадь треугольника:
M = 15 (обозначены красным)
N = 34 (обозначены синим)
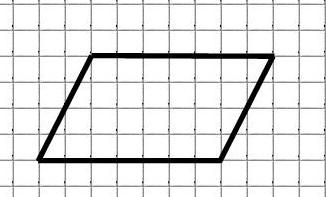
Ещё пример. Найдём площадь параллелограмма:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
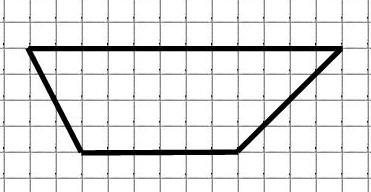
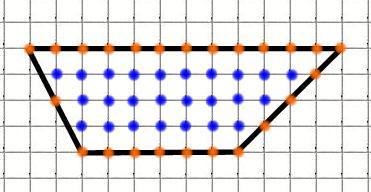
Найдём площадь трапеции:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
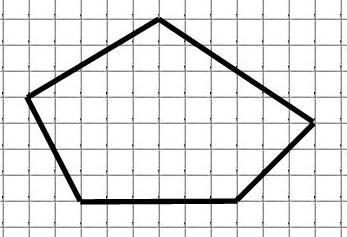
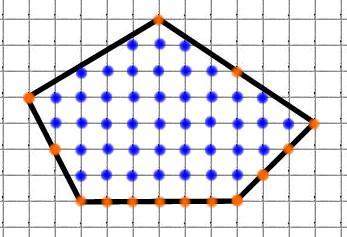
Найдём площадь многоугольника:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
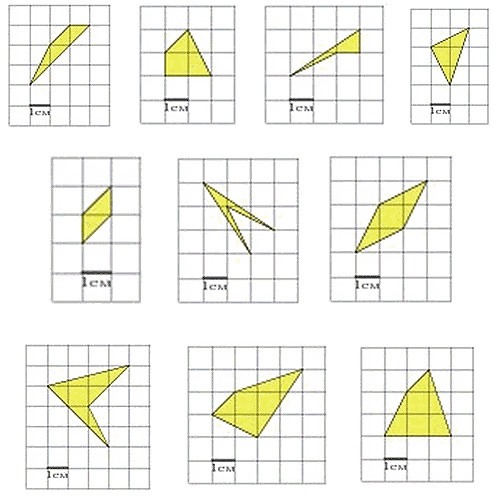
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ«.
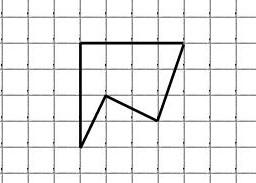
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Презентация к уроку
Авторы: Куровская Юлия, Шагаева Диана.
Девиз проекта:
“Если вы хотите научиться плавать, то смело входите в воду.
а если хотите научиться решать задачи, то решайте их”.
Д. Пойя.
Выбор темы проекта не случаен. Способы нахождения площади многоугольника нарисованного на “клеточках” очень интересная тема.
Мы знаем разные способы выполнения таких заданий: способ сложения, способ вычитания и др.
Нас очень заинтересовала эта тема, мы изучили много литературы и к нашей огромной радости нашли еще один способ, способ не известный по школьной программе, но способ замечательный! Вычисление площади, используя формулу, выведенную австрийским ученым – математиком Георгом Пиком.
Мы решили изучить формулу Пика, при помощи которой выполнять задания на нахождении площади очень легко!
Решили поделиться нашим открытием с одноклассниками, учащимися других школ, создать электронную презентацию.
Цель исследования
1. Изучение формулы Пика.
2. Расширение знаний о многообразии задач на клетчатой бумаге, о приёмах и методах решения этих задач.
Задачи:
1. Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
2. Проанализировать и систематизировать полученную информацию
3. Создать электронную презентацию работы для представления собранного материала одноклассникам
4. Сделать выводы по результатам работы.
5. Подобрать наиболее интересные, наглядные примеры.
Методы исследования:
3. Анализ и классификация информации
4. Сравнение, обобщение
5. Изучение литературных и Интернет-ресурсов
Георг Пик – австрийский ученый – математик. Пик поступил в университет в Вене в 1875 году. Свою первую работу опубликовал в возрасте 17 лет. Круг его математических интересов был чрезвычайно широк. 67 его работ посвящены многим разделам математики, таким как: линейная алгебра, интегральное исчисление, геометрия, функциональный анализ, теория потенциала.
Широко известная Теорема появилась в сборнике работ Пика в 1899 году.
Теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.
Формула Пика, формула вычисления площади многоугольника, изображенного на бумаге в клетку, полезна при решении заданий ЕГЭ и ОГЭ. Именно, поэтому, она нас очень заинтересовала.
Формула Пика — классический результат комбинаторной геометрии и геометрии чисел.
По теореме Пика площадь многоугольника равна:
Г – число узлов решетки на границе многоугольника
В – число узлов решетки внутри многоугольника.
Первым делом мы поставили задачу: изучить, что такое узлы решетки и как правильно вычислять их количество. Оказалось, это очень просто. Приведем несколько примеров.
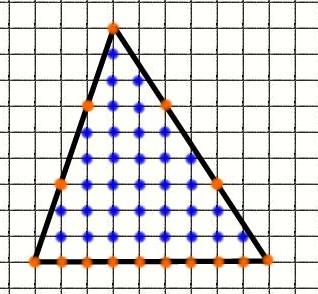
Пусть дан произвольный треугольник. Узлы на границе изображены оранжевым цветом, узлы внутри изображены синим цветом. Найти узлы и подсчитать их количество очень легко.
В данном случае Г= 15, В = 35
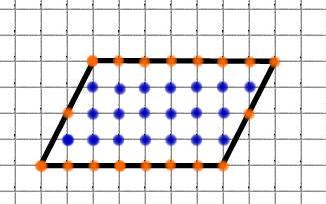
Пример №2 Узлов на границе 18, т.е. Г = 18, узлов внутри 20, В = 20.
И еще один пример. Дан произвольный многоугольник. Считаем узлы на границе. Их 14. Узлом внутри многоугольника 43. Г = 14, В = 43.
С первой задачей мы справились!
Второй этап нашей работы: вычисление площадей многоугольников.
Рассмотрим несколько примеров.
Пример №1.
Г = 14, В = 43, S =
+ 43 – 1 = 49
Пример №2.
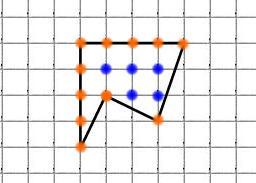
Г = 11, В = 5, S =
+ 5 – 1 = 9,5
Пример №3.
Г = 15, В = 22, S =
+ 22 – 1 = 28,5
Пример №4.
Г = 8, В = 16, S =
+ 16 – 1 = 19
Пример №5
Г = 10, В = 30, S =
+ 30 – 1 = 34
На рассмотрение пяти примеров мы затратили всего 1-2 минуты. Вычислять площадь по формуле Пика не только быстро, но и очень легко!
Но перед нами встал очень серьезный вопрос:
Можно ли доверять теореме Пика?
Получаются ли одинаковые результаты при вычислении площадей разными способами?
Найдем площади многоугольников по формуле Пика и обычным способом, применяя формулы геометрии и способы достроения или разбиения на части. Вот какие результаты мы получили:
Пример №1.
Вычислим площадь многоугольника по формуле Пика:
Подсчитаем количество узлов на границе и внутри. Г = 3, В = 6.
Вычислим площадь: S = 6 + 
Пример №2.
Вычислим площадь по формуле Пика.
Г = 4, В = 9, S = 9 + 
Достроим до прямоугольника.
Площадь прямоугольника равна: 5 * 4 = 20, S1 = 2 * 1 = 2, S2 = 
Площадь прямоугольника равна
S = 20 – 2 – 3 – 2 – 1,5 – 2,5 = 10
Мы снова получили одинаковые результаты.
Рассмотрим еще один пример.
Пример №3
Вычислим площадь по формуле Пика.
Г = 5, В = 6, S = 6 + 
Вычислим площадь, используя способ достроения.
Площадь прямоугольника равна 5·4 = 20
S1 = 2 * 1 = 2, S2 = 



S7 = 
В презентации мы рассмотрели три примера, но на самом деле мы рассмотрели очень много самых разных примеров. Результат всегда был один и тот же: Вычисление площади по формуле Пика и другими способами дает одинаковый результат.
Вывод: формуле Пика можно доверять! Она дает точный результат.
И еще один вопрос встал перед нами: какой способ вычисления наиболее рациональный, наиболее удобный для использования?
Чтобы ответить на этот вопрос, достаточно использовать всю предыдущую работу. Но рассмотрим еще три примера, которые окончательно позволят получить ответ на наш вопрос.
При помощи формулы Пика легко вычислить площадь многоугольника даже самой причудливой формы. Рассмотрим пример:
Вывод однозначный: наиболее рациональный способ вычисления площади многоугольника, изображенного на бумаге в клетку: формула Пика!
Предлагаем каждому из вас вычислить площадь многоугольника, используя формулу Пика:
— вычислите количество узлов на границе. Они изображены желтым цветом.
— вычислите количество узлов внутри, красный цвет.
— Подставьте в формулу, назовите результат. Вы за одну минуту вычислили площадь.
Итак, формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:
Для вычисления площади многоугольника, нужно знать всего одну формулу:
Формула Пика очень проста для запоминания.
Формула Пика очень удобна и проста в применении.
Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.
Применяя формулу Пика легко выполнять задание ЕГЭ и ОГЭ.
Приведем несколько примеров вычисления площади из вариантов ЕГЭ – 2015.
Мы решили научить пользоваться формулой Пика учащихся 9 – 11 классов нашей школы. Провели фестиваль “Формула Пика”.
Все учащиеся с большим интересом познакомились с презентацией, научились пользоваться формулой Пика.
За 30 минут практической работы учащиеся выполнили большое количество заданий. Каждый учащийся получил памятку “Формула Пика”.
Мы помогли им в подготовке к ЕГЭ и ОГЭ!
Спустя месяц работы, мы провели опрос учащихся 9–11 классом.
Задали следующие вопросы:
Вопрос №1:
Формула Пика – это рациональный способ вычисления площади многоугольника?
Вопрос №2:
Вы пользуетесь формулой Пика?
Наша работа не прошла даром! Мы довольны!
Презентацию нашего проекта мы разместили в сети Интернет. Много просмотров и скачиваний нашей работы.
Мы оформили альбом “Формула Пика”. Им постоянно, особенно первое время, пользовались учащиеся нашей школы.
Результаты работы над проектом:
Предлагает вам выполнить два задания, чтобы вы убедились в рациональности нашей работы.
Конспект к презентации «Теорема Пика»
Ищем педагогов в команду «Инфоурок»
Муниципальное бюджетно образовательное учреждение
«средняя общеобразовательная школа №11»
Применение формулы Пика
Сумпатова Анастасия учащаяся 6 «б» класса МБУ СОШ № 11
МБУ СОШ№11 Филипова Ольга Юрьевна
1.2 Задачи исследования…………………стр.4
Создатель Теоремы Пика………………стр.5-7
Теорема. Формула и её свойства…………стр. 8
Доказательство Теоремы Пика………….. стр. 9
Фигуры посложнее………………………. Стр.13
Задачи с интересными фигурами……….. стр. 14
Знают ли мои сверстники о формуле…… стр.15
Узнать что такое Теорема Пика и понять её свойства.
Применить Теорему Пика в задачах.
Узнать нужна ли она в ЕГЭ.
Выявить в ходе опроса что знают о Теореме мои сверстники.
Для достижения поставленной цели предусматриваем решение следующих задач:
Подобрать подходящую информацию.
Показать на практике работу Теоремы Пика.
Учебник математики для 5 классов. М.Н. Башмаков
Каждая теорема имеет свою интересную и неповторимую историю. Конечно хочется узнать, как можно больше. Всем известно, что история начинается с создателя. Именно он создал и изучил свойства своего открытия. Теорема Пика не стала исключением. Поэтому давайте знакомиться с её сюжетом.
Создатель Теоремы Пика
Пик поступил в университет в Вене в 1875 году. Уже в следующем году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику, окончил в 1879 г. универститет, получив возможность преподавать оба эти предмета. В 1877 году из Дрезденской Высшей технической школы переехал Лео Кёнигсбергер, который занял кафедру в венском университете. Он стал руководителем Пика, и 16 апреля 1880 г. Пик защитил докторскую диссертацию “О классе абелевых интегралов”. Вторым экзаменатором на защите был Эмиль Вейра.
После получения докторской степени Пик был назначен помощником Эрнста Маха в пражском университете Карла-Фердинанда. Мах переехал из Граца, где он был профессором математики, в Прагу в 1867 году, чтобы занять там кафедру физики. Он, как и Пик, учился в университете в Вене и, к тому времени как Пик стал его помощником, считался одним из ведущих европейских ученых. Пик теперь хотел читать лекции в Праге, и для того
hyperelliptischer Differentiale durch Logarithmen, после чего в 1881 году получил право читать лекции в Праге.
За исключением академического 1884-85 года, который Пик провел в Лейпцигском университете, учась у Кляйна, он оставался в Праге до конца своей карьеры. В 1888 г. он был назначен экстраординарным профессором математики, затем — ординарным профессором (полным профессором) в 1892 году в немецком университете в Праге. Круг его математических интересов был чрезвычайно широк, и 67 его работ посвящены многим темам, таким как линейная алгебра, теория инвариантов, интегральное исчисление, теория потенциала, функциональный анализ и геометрия. Тем не менее более половины его работ связаны с функциями комплексного переменного, дифференциальными уравнениями и дифференциальной геометрией. Такие термины как матрица Пика, интерполяция Пика — Неванлинны, и лемма Шварца — Пика используются иногда и сегодня. Он больше всего известен, однако, своей теоремой Пика, которая появилась в его восьмистраничной работе 1899 года Geometrisches zur Zahlenlehre, опубликованной в Праге в Sitzungber, Lotos, Naturwissen Zeitschrift.
После того как Пик вышел в отставку в 1927 г., он получил звание почетного профессора и вернулся в Вену, город, в котором он родился. Тем не менее, в 1938 г. он вернулся в Прагу после аншлюса 12 марта, когда немецкие войска вошли в Австрию. В конце сентября 1938 г. правительство Праги попросили отдать Германии все районы Чехии и Моравии, население которых на 50 или
более процентов составляли немцы. Лидеры Чехословакии ушли в отставку, но не согласились на это, однако те, кто пришел им на смену, отдали эти регионы Германии. Гитлеровская армия вторглась в Прагу 14 марта 1939 г., и Гитлер оставил здесь своего представителя для того, чтобы управлять страной. Пик был избран членом Чешской академии наук и искусств, но после того как нацисты пришли в Прагу, он был исключен из академии. Нацисты создали лагерь Терезиенштадт в Северной Богемии 24 ноября 1941 г. для размещения престарелых, привилегированных и знаменитых евреев.

















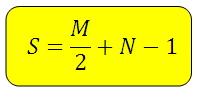
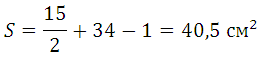
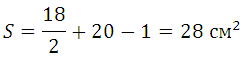
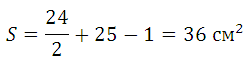
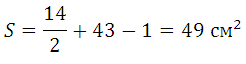
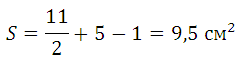

 + 43 – 1 = 49
+ 43 – 1 = 49 + 5 – 1 = 9,5
+ 5 – 1 = 9,5 + 22 – 1 = 28,5
+ 22 – 1 = 28,5 + 16 – 1 = 19
+ 16 – 1 = 19 + 30 – 1 = 34
+ 30 – 1 = 34




