Как играть в игру матрица
Мы поиграли в технодемо The Matrix Awakens. Это будущее видеоигр — и, скорее всего, оно вам не понравится
Чего у Epic Games не отнять, так это эффектных презентаций своих технологий. Прошлогодний стрим с показом Unreal Engine 5 еще долго отдавался эхом по интернету, а в качестве первого широкого доступного демо компания выпустила совместный с Warner Bros. проект по «Матрице» — кто-нибудь вообще презентовал свои технологии круче? При этом The Matrix Awakens смогла показать не только поразительную картинку, но и будущее, в котором мы можем оказаться. И похоже, что игрокам в нем будет настолько же невесело, как и людям под гнетом машин в фильме.
Новые технологии в Unreal Engine 5 позволят достигать небывалого уровня качества трехмерной графики вполне доступными средствами — достаточно иметь мощный компьютер, минимальные навыки и большое желание. Своей прошлогодней презентацией движка Epic Games взорвала интернет: обсуждения не утихали вплоть до выхода консолей нового поколения. Теперь сделать кинематографичную игру с правильным освещением, высокой детализацией объектов и процедурной анимацией сможет любой умелец, который достаточно разбирается в программировании или имеет много времени. Благодаря этим возможностям инди-игры начнут выглядеть гораздо круче, жизнь разработчиков упростится, а игроки получат в разы больше красивых и интересных игр. Или нет?
С другой стороны, какая разница, ведь у нас тут «Матрица» возвращается! Маркетинг Warner Bros. всерьез пытается показать, что именитая франшиза вышла из комы, заигрывая с ожиданиями зрителей в трейлерах. Epic Games, в свою очередь, смогла подарить фанатам то, о чем двадцать лет назад можно было только мечтать — возможность прогуляться по фотореалистичному городу из фильмов. Вот у нас тут здание, где работал Нео; вот банк, в котором они с Тринити разносили колонны; вот площадка, где происходил мощнейший замес с агентами Смитами во второй части — все это действительно круто.
Вышедшая сегодня бесплатно для всех владельцев PlayStation 5 и Xbox Series X/S The Matrix Awakens стала вторым широкодоступным проектом на Unreal Engine 5 (первым был Fortnite), и вряд ли можно придумать презентацию эффектнее
Демо разделено на две части: первая состоит ролика с Киану Ривзом и Кэри-Энн Мосс, участвующих в постановочной погоне, где игрок в основном наблюдает за происходящим, а вторая — из возможности исследовать город. Получилась почти GTA, но без насилия: можно ходить по окрестностям и садиться в любую припаркованную машину, но нельзя сбивать пешеходов и выкидывать водителей из их автомобилей; по размеру Мега-Сити сравним с целым Вайс-Сити.
Хотя Carmageddon устроить нельзя, машины ломаются довольно красиво
И вроде бы выглядит все это просто потрясающе. В Digital Foundry уже назвали демо «обязательным к ознакомлению», расхвалили применяемые технологии и отметили, что с их помощью теперь даже небольшие команды смогут делать огромные миры.
Здесь стоит оговориться, что The Matrix Awakens — не полноценная игра, никогда ей не будет и не претендует на это. Но вот судить о возможностях независимых разработчиков, которые у них появятся с переходом на Unreal Engine 5, не только можно, но и нужно — к этому подталкивает сама Epic.
Итак, что же смогла сделать «сравнительно небольшая команда» из Epic? Если говорить в цифрах, то вышел город площадью около 16 квадратных километров с 45 тысячами машин, из которых 17 тысяч находится на дорогах и изображают траффик. По местности разбросано 7 тысяч зданий, мимо которых ходит 35 тысяч горожан, а на все это сверху светит солнце как источник глобального освещения; ночью его заменяют фонари и свет из окон домов — никаких искусственных дополнительных источников. Звучит очень круто, но что это значит на деле?
На раскиданных по городу табличках есть интересные факты о культовых сценах и их создании
Естественно, для создания такого объема ассетов использовалась процедурная генерация. В итоге большая часть города выглядит невыразительно, а внимание привлекают лишь знакомые по фильмам здания. Впрочем, в этом нет ничего плохого — примерно то же можно сказать про любой открытый мир. А вот гигантомания, которая и без того уже почти десять лет преследует разработчиков и их чересчур огромные игры, похоже, затронет и инди. Если теперь любой сможет делать огромные пустые города, то хватит ли серверов Epic Games Store и Steam, чтобы хранить столько народного творчества?
Ключевой вопрос любого открытого мира — наполненность. Разумеется, The Matrix Awakens не является полноценной игрой, но мы ведь все понимаем, что если маленькой команде теперь хватит ресурсов на создание огромного мира, то прорывные технологии все равно не заполнят его деталями и контентом?
Теория игр. Матричные игры. Онлайн калькулятор
С помощю этого онлайн калькулятора можно решить задачу теории игр. Для решения задачи теории игр задайте количество строк и количество столбцов матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Предупреждение
Теория игр − теоретическая часть
Бывают ситуации, в которых сталкиваются интересы двух и более сторон. При этом эффективность принимаемого решения одной стороны зависит от действий другой стороны. Такие ситуации называются конфликтными. Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной стороны на определенную величину приводит к уменьшению выигрыша другой стороны на такую же величину. Математическая модель таких ситуаций описывается матричной игрой. Участники игры (т.е. лица, принимающие решение) называются игроками. Принятие игроком того или иного решения в процессе игры и его реализация называется ходом. Ходы могут быть личными (т.е. сознательными) и случайными. Стратегия игрока − осознанный выбор одного из множества вариантов его действий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистых стратегий, а у второго игрока n чистых стратегий. Если множество стратегий игроков конечный, то игра называется конечной, а если хотя бы у одного игрока множество стратегий бесконечно, то игра называется бесконечной. Стратегия игрока называется оптимальной, если она обеспечивает данному игроку (при многократном повторении) максимально возможный средний выигрыш или минимально возможный средний проигрыш.
Игры, в которых учавствуют 2 игрока, называются парными, а игры с большим числом участников − множественными. Если в парной игре выигрыш одной стороны точностью совпадает с проигрышем другой стороны, то игра называется игрой с нулевой суммой.
В зависимости от вида функций выигрышей, игры бывают матричные, биматричные, непрерывные, выпуклые и др.
Рассмотрим матричную игру двух участников с нулевой суммой и конечным числом возможных ходов.
Решение матричной игры в чистых стратегиях
Пусть игроки A и B распологают конечным числом возможных действий (чистых стратегий). Обозначим их через 





Таким образом игра с нулевой суммой однозначно определяется матрицей
которая называется платежной матрицей или матрицей выигрышей. Строки матрицы (1) определяют стратегии первого игрока (

Игра проходит партиями. Партия начинается с первого игрока. Он выбирает некоторую строку i матрицы. В ответ на это второй игрок выбирает некоторый столбец j. На этом заканчивается партия и второй игрок платит первому сумму aij, если aij>0 или первый игрок платит сумму aij второму игроку, если aij Теорема 1. В матричной игре нижняя цена игры не превосходит верхней цены, т.е. α ≤ β.
Если для чистых стратегий Ak и Bl игроков A и B имеет место равенство α = β, то пару чистых стратегий (Ak,Bl) называют седловой точкой матричной игры а γ=α = β чистой ценой игры. Элемент akl называют седловым элементом платежной матрицы.
Заметим, что отклонение игрока A от максимальной стратегии Ak ведет к уменьшению его выигрыша, а отклонение игрока B от минимальной стратегии Bl ведет к увеличению его проигрыша. Поэтому Ak и Bl являются оптимальными чистыми стратегиями игроков A и B, соответственно.
Тройку (Ak, Bl, γ) называют решением матричной игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.
Решение матричной игры в смешанных стратегиях
Если матричная игра не имеет седловой точки, то α ≠ β, и, Теорему 1, получим: α * и q * называются оптимальными, если они образуют седловую точку для платежной функции M(p,q), т.е.
Значение платежной функции при оптимальных смешанных стратегиях p * и q * называют ценой игры:
Теорема 2 (Основная теорема теории матричных игр). В любой матричной игре у игроков есть оптимальные смешанные стратегии.
Доказательство. Пусть игра имеет платежную матрицу
где все элементы положительны.
Математическое ожидание выигрыша игрока A равна:
При любом выборе игроками своих смешанных стратегий p и q, математическое ожидание будет положительным, так как все элементы aij платежной матрицы положительны, pi неотрицательные числа и среди них есть хотя бы одно положительное число, qj неотрицательные числа и среди них есть хотя бы одно положительное число.
так как aij >0, i=1,2. m, j=1,2. n. Поскольку α>0 и γ не может быть меньше нижней цены игры, то γ ≥ α, а так как α>0, то γ >0.
Пусть игрок A выбирает такую стратегию p, что математическое ожидание его выигрыша независимо от того, какую стратегию выбирает игрок B было не меньше некоторой величины γ:
где pi >0, i=1,2. m, 
Преобразуем систему нерравенств (3), введя новые обозначения:
Разделим все неравенства системы (3) на положительное число γ. Тогда имеем:
Цель игрока A − максимизировать свой гарантированный выигрыш γ или минимизировать величину
Таким образом, приходим к следующей задаче линейного программирования:
Сделав аналогичные рассуждения с позиции игрока B, получим следующую задачу линейного программирования:
Покажем, что задачи линейного программирования (4) и (5) имеют допустимые решения. Так как aij >0, то можно подобрать достаточно большие положительные числа yi, i=1,2. m так, чтобы выполнялись неравенства (4b). Значит задача линейного программирования (4) имеет допустимое решение.
Допустимое решение задачи линейного программирования (5) является нулевой вектор. Таким образом, пары двойственных задач линейного программирования (4) и (5) имеют допустимые решения. Тогда, согласно теории двойственных задач линейного программирования, обе эти задачи имеют оптимальные планы 

Найдем оптимальные смешанные стратегии игроков:
  , , |
  . . |
Пара 
Если в матрице 
Математическое ожидание выигрыша игрока A с платежной матрицей A(aij):
 |
Математическое ожидание игрока A с платежной матрицей A’(aij+r):
 |
   |
Игра с платежной матрицей A’ имеет седловую точку 
 |
Следовательно, игра с платежной матрицей A также имеет седловую точку 
Для рассмотрения численного примера матричной игры, введите в калькуляторе в начале страницы элементы матрицы и нажмите на кнопку вычислить. Онлайн калькулятор выдаст подробное рашение задачи.
Матричные игры: примеры решения задач
Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.
Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.
Теперь обо всём по порядку и подробно.
Платёжная матрица, чистые стратегии, цена игры
В матричной игре её правила определяет платёжная матрица.
В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.
Составим платёжную матрицу:

Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает «орёл» или «решка». Если одновременно выпали «орёл» и «орёл» или «решка» или «решка», то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:

Как происходит выбор стратегии в матричной игре?
Вновь посмотрим на платёжную матрицу:

Пример 1. Дана матричная игра с платёжной матрицей
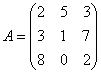
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.
Итак, гарантированный выигрыш первого игрока:

Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:

Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так:

Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:

Ещё пример из этой же серии.
Пример 2. Дана матричная игра с платёжной матрицей

Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Седловая точка в матричных играх
Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.
Таким образом, если 


В этом случае матричная игра имеет решение в чистых стратегиях.
Пример 3. Дана матричная игра с платёжной матрицей

Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Решить задачу на матричную игру самостоятельно, а затем посмотреть решение
Пример 4. Дана матричная игра с платёжной матрицей

Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Матричные игры с оптимальной смешанной стратегией
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.
Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.
Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.
Если первый игрок использует чистые стратегии с вероятностями 


Если второй игрок использует чистые стратегии с вероятностями 



Если уже подзабыто произведение матриц, то следует повторить материал.
Пример 5. Дана матричная игра с платёжной матрицей

Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока), если смешанная стратегия первого игрока 

Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока) оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора смешанной стратегии второго игрока:
Оптимальной смешанной стратегией первого игрока называется такая смешанная стратегия 

Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия 

По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):


В таком случае для функции E существует седловая точка, что означает равенство 
Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования, то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.
Сведение матричной игры к задаче линейного программирования
Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.
Функция цели в прямой задаче линейного программирования:

Система ограничений в прямой задаче линейного программирования:
Функция цели в двойственной задаче:

Система ограничений в двойственной задаче:
Оптимальный план прямой задачи линейного программирования обозначим

а оптимальный план двойственной задачи обозначим
Линейные формы для соответствующих оптимальных планов обозначим 

а находить их нужно как суммы соответствующих координат оптимальных планов.
В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:


Математики-теоретики доказали, что цена игры следующим образом выражается через линейные формы оптимальных планов:

то есть является величиной, обратной суммам координат оптимальных планов.
Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:


Пример 6. Дана матричная игра с платёжной матрицей

Найти цену игры V и оптимальные смешанные стратегии 

Решение. Составляем соответствующую данной матричной игре задачу линейного программирования:
Получаем решение прямой задачи:

Находим линейную форму оптимальных планов как сумму найденных координат:

Получаем решение двойственной задачи:

Находим линейную форму оптимальных планов как сумму найденных координат:


Находим оптимальную смешанную стратегию первого игрока:

Находим оптимальную смешанную стратегию второго игрока:

Игры с матрицей 2 Х 2
Пусть дана игра с платёжной матрицей
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях, как показано в параграфах 1 и 2.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:

Формула для нахождения оптимальной смешанной стратегии второго игрока:

Формула для нахождения цены игры:

Пример 7. Дана матричная игра с платёжной матрицей

Найти оптимальные смешанные стратегии игроков и цену игры.
Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:

Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:


Составление матричной игры
Матричная игра, седловая точка, чистые стратегии, смешанные стратегии. А для чего всё это? Рассмотрим на примере, как с помощью матричных игр решаются экономические задачи.
Пример 8. Составить матричную игру для следующей задачи.
| B 1 | B 2 | B 3 | B 1 | |
| A 1 | 3 | 3 | 6 | 8 |
| A 2 | 9 | 10 | 4 | 2 |
| A 3 | 7 | 7 | 5 | 4 |

Далее составляется и решается задача линейного программирования. Это мы уже умеем.











