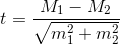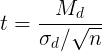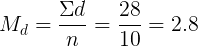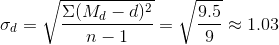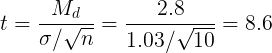Как интерпретировать результаты критерия стьюдента
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
t-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ
– общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

1. История разработки t-критерия
Данный критерий был разработан Уильямом Сили Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
3. В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
4. Как рассчитать t-критерий Стьюдента?
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
5. Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
6. Пример расчета t-критерия Стьюдента
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА
– одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.

1. История разработки t-критерия
t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется парный t-критерий Стьюдента?
3. В каких случаях можно использовать парный t-критерий Стьюдента?
Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.
Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.
Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.
4. Как рассчитать парный t-критерий Стьюдента?
Парный t-критерий Стьюдента рассчитывается по следующей формуле:
5. Как интерпретировать значение t-критерия Стьюдента?
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p
3. Найдем среднее квадратическое отклонение разностей от средней по формуле:
4. Рассчитаем парный t-критерий Стьюдента:
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
Динамические ряды могут быть моментными, когда величины ряда характеризуют явление на какой-то определенный момент времени (штаты, койки, вновь выявленные больные при медосмотрах и т.д.) и интервальными, когда явление рассматривается за определенный период (число родившихся и умерших за год, число поступивших больных в стационар, число бытовых травм за месяц и др.).
Для характеристики динамического ряда используют 3 основных показателя:
Рассмотрим методику анализа динамического ряда на примере изменения показателя общей смертности в России с 1940 по 1995 годы:
Пример расчета:
2) Темп роста = последующий уровень х 100% / предыдущий уровень
1940-1960 гг. = 7,4 х 100 / 20,6 = 35,9%
1970-1960 гг. = 8,7 х 100 / 7,4 = 117,6%
1980-1970 гг. = 11 х 100 / 8,7 = 126,4%
3) Темп прироста = абс. прирост х 100 / предыдущий уровень
1970-1960 гг. = 1,3 х 100 / 7,4 = 17,6
1980-1970 гг. = 2,3 х 100 / 8,7 = 26,4
Многочисленные наблюдения за длительный промежуток времени не всегда позволяют выявить определенную тенденцию в динамике. Такую возможность дает применение методов выравнивания динамических рядов. К ним относятся:
1. Приведение рядов к одному основанию путем вычисления показателей наглядности. Динамика в этом случае выразится наиболее ярко.
2. Укрупнение интервалов, которое заключается в суммировании данных за ряд периодов. В результате получаются итоги за более продолжительные отрезки времени и тем самым сглаживаются случайные колебания и более четко определяется характер динамики.
3. Сглаживание путем групповой и скользящей средней. Периоды времени укрупняются и для них вычисляется средняя величина, характеризующая укрупненный период. Этим достигается большая ясность изменений во времени.
Интересен метод скользящей средней, который часто применяется для характеристики сезонных колебаний. Для этого каждый уровень ряда заменяется средней из данного уровня и соседних с ним. Обычно суммируются последовательно три члена ряда, но можно брать и больше. Важно, что средняя получается для каждого уровня динамического ряда.
23.Средние величины, методика расчета средней, среднеквадратического отклонения, ошибки средней и коэффициента вариации. Нормальное распределение вариационного ряда, Кривая Гаусса-Лапласа, мода и медиана.
24.Средние величины, их значение и применение в практической деятельности врача. Понятие о норме, среднее квадратическое отклонение, ошибка средней и коэффициент вариации (Сv). Их значение и применение.
25.Классификация средних величин. Вариационные ряды его виды и элементы. Правила построения вариационного сгруппированного ряда. Определение средней арифметической простой и взвешенной. Примеры использования средних величин в лечебной практике.
26.Значение и применение ошибки средней арифметической величины и относительного показателя. Определение ошибки относительного показателя, если он равен 0 или 100%. Определение достаточного числа наблюдений для получения достоверного результата исследования.



Дата добавления: 2019-07-15 ; просмотров: 195 ; Мы поможем в написании вашей работы!
Классические методы статистики: t-критерий Стьюдента
 |
| У. Госсет, автор t-критерия. Рисунок из Wikipedia |
Критерий Стьюдента t относится к одному из наиболее давно разработанных и широко используемых методов статистики. Чаще всего он применяется для проверки нулевой гипотезы о равенстве средних значений двух совокупностей, хотя существует также и одновыборочная модификация этого метода. В данном сообщении я продемонстрирую, как статистические тесты, основанные на критерии Стьюдента, можно реализовать в R.
Одновыборочный t-критерий
В общем виде проверка (= тест) этой гипотезы выполняется при помощи t-критерия, который рассчитывается как отношение разницы между выборочным средним и известным значением к стандартной ошибке выборочного среднего:
Сравнение двух независимых выборок
stature можно расшифровать как «зависимость суточного потребления энергии ( expend ) от статуса пациентки ( stature )».
Сравнение двух зависимых (= парных) выборок
Если нулевая гипотеза заключается в равенстве истинного эффекта нулю, формула для парного критерия Стьюдента примет вид
Индивидуальные разницы в потреблении энергии у этих женщин составляют:
Усреднив эти индивидуальные разницы, получим
Задача заключается в том, чтобы оценить, насколько статистически значимо эта средняя разница отличается от нуля. Применим парный критерий Стьюдента (обратите внимание на использование аргумента paired = TRUE ):
Как видим, рассчитанное программой P-значение оказалось намного меньше 0.05, что позволяет нам сделать заключение о наличии существенной разницы в потреблении энергии у исследованных женщин до и после менструации. Истинная величина эффекта (в абсолютном выражении) с вероятностью 95% находится в интервале от 1074.1 до 1566.8 кДж/сутки.
t-критерий Стьюдента для проверки гипотезы о средней и расчета доверительного интервала в Excel
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:
Для расчета двустороннего t-значения используем функцию:
Для двустороннего t используем удвоенное значение вероятности:
В результате получим:
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
Этапы статистического вывода (statistic inference)
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
Внесите исходные данные группы
Вы можете внести данные для расчета критерия Т-Стьюдента поочередно вручную или скопировать их из вашего Excel файла.
Внесите исходные данные группы
Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.
Критические точки распределения Стьюдента
| Число степеней свободы k | Уровень значимости α (двусторонняя критическая область) | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3.14 | 3.71 | 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ∞ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости α (односторонняя критическая область) | ||||||
Условия применения t-критерия Стьюдента
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.