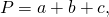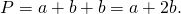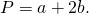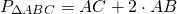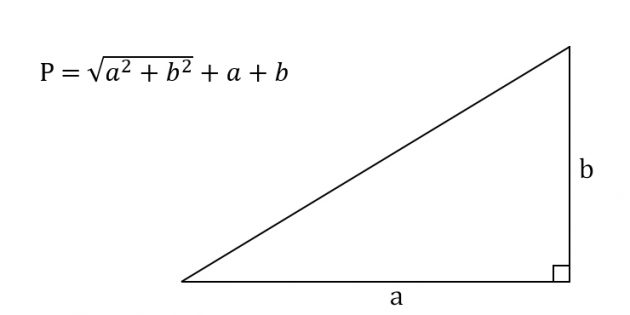Как искать периметр равнобедренного треугольника
Как найти периметр треугольника
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
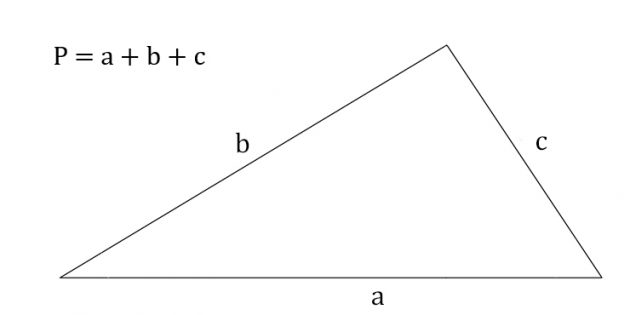
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Нахождение периметра треугольника: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.
Периметр равнобедренного треугольника
Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание и боковую сторону.
В общем случае формула для нахождения периметра треугольника выглядит так:
где a, b и c — длины сторон треугольника.
формулу можно упростить:
Таким образом, периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны:
Соответственно, периметр равнобедренного треугольника ABC можно найти по формуле:
(здесь AC — основание, AB — боковая сторона).
1) Найти периметр равнобедренного треугольника, если его основание равно 4 см, а боковая сторона — 9 см.
Здесь а=4 см, b=9 см. По формуле Р=а+2b имеем: P=4+2∙9=22 (cм).
2) Периметр равнобедренного треугольника равен 170 см, а его основание — 60 см. Найти боковую сторону треугольника.
Здесь а=60 см, Р=170 см. По формуле Р=а+2b, 2b=Р-а, b=(Р-а):2, b=(170-60):2=55 (см).
Задача нахождения периметра равностороннего треугольника решается еще проще. Её мы рассмотрим в следующий раз.
Периметр и площадь треугольника
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
где P — это периметр треугольника, a, b и c — его стороны.
Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.
Как найти периметр треугольника
Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.
Периметр треугольника
Периметр треугольника — это сумма длин всех его сторон.
Треугольник — это геометрическая фигура, которая состоит из трех точек (вершин), не лежащих на одной прямой. Эти точки попарно соединены тремя отрезками, которые называются сторонами (ребрами) многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры. Каждая из предложенных формул опирается на те величины, которые нам уже известны.
Способы нахождения
По трем сторонам
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:
где a, b и с — это стороны треугольника.
В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:
где a — основание фигуры, а b и с — равные ребра.
Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:
где a — это любая сторона фигуры.
По площади и радиусу вписанной окружности
Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:
где S — площадь фигуры, r — радиус вписанной в нее окружности.
По двум сторонам и углу между ними
Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.
Теорема косинусов выглядит так:
где α — известный угол.
Тогда формула для расчета периметра всей фигуры в этом случае:
По боковой стороне и высоте (для равнобедренного)
Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.
Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:
где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.
Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.
По двум катетам (для прямоугольного)
Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).
где a и b — катеты треугольника.
Подставляем значение c в формулу для нахождения периметра и получаем:
Примеры решения задач
Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.
Задача №1
Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.
Решение:
Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.
Задача №2
Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.
Решение:
Для данного случая подходит формула P=a+2b, подствляем значения: \(P=6+4\times2 = 14\) см.
Задача №3
Решение:
Задача №4
Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.
Решение:
Задача №5
Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.
Решение:
В формулу \(P=\sqrt