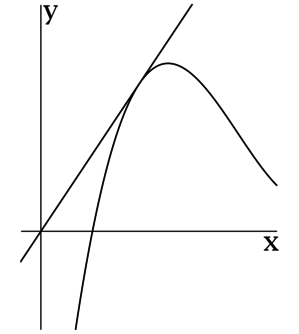Как искать угловой коэффициент функции

Линейная функция

Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

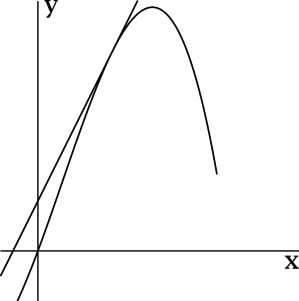
Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой это не выполняется: значению соответствует бесконечно много значений у.

Если прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

Значит, наша прямая проходит через точки и

Зачем изучать линейную функцию?

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Источник

Угловой коэффициент касательной как значение производной в точке касания

\[<\large>\] где \(x_o\) — абсцисса точки касания прямой и кривой.

Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.

Основные моменты

Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.

Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.

Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.

Как подготовиться к экзамену?

Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.

Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.

Источник

Линейная функция ее свойства и график. Угловой коэффициент линейной функции

Линейная функция

Линейная функция – это функция вида:

здесь k и b являются действительными числами.

Свойства линейной функции

Линейная функция имеет следующие свойства:

Угловой коэффициент линейной функции

Коэффициент k в формуле линейной функции называется угловым коэффициентом.

Угловой коэффициент определяет угол между графиком линейной функции и положительным направлением оси абсцисс.

График линейной функции

График линейной функции есть прямая. Вот график линейной функции y = 2x + 1

здесь угловой коэффициент больше нуля, угол прямой линии y = 2x + 1 с положительным направлением оси x – острый.

Как изменяется график линейной функции в зависимости от числа b в формуле линейной функции y = kx + b? Если b увеличивать, график смещается вверх, если число b уменьшать, то график y = kx + b смещается вниз.

График линейной функции y = kx + b построить вы можете сами прямо сейчас с помощью построителя графиков. Выберете в нём вид функции «Линейная: y = k * x + b» и нажмите кнопку «Построить график». Проведите эксперименты: устанавливайте угловые коэффициенты больше и меньше нуля, меняйте значения числа b и посмотрите, как будет изменяться график линейной функции.

Источник

Как определить угловой коэффициент по графику. Как найти угловой коэффициент прямой

В математике одним из параметров, описывающих положение прямой на декартовой плоскости координат, является угловой коэффициент этой прямой. Этот параметр характеризует наклон прямой к оси абцисс. Чтобы понять, как найти угловой коэффициент, сначала вспомним общий вид уравнения прямой в системе координат XY.

Решение: Преобразуем исходное уравнение.

Ответ: Искомый угловой коэффициент данной прямой равен 2.

В случае, если в ходе преобразований уравнения мы получили выражение типа x = const и не можем в результате представить y в виде функции x, то мы имеем дело с прямой, параллельной оси Х. Угловой коэффициент подобной прямой равен бесконечности.

Для прямых, которых выражены уравнением типа y = const, угловой коэффициент равняется нулю. Это характерно для прямых, параллельных оси абцисс. Например:

Решение: Приведем исходное уравнение к общему виду

Из полученного выражения выразить y невозможно, следовательно угловой коэффициент данной прямой равен бесконечности, а сама прямая будет параллельна оси Y.

Геометрический смысл

Для лучшего понимания обратимся к картинке:

Решая задачу, как найти угловой коэффициент прямой, мы находим тангенс угла между ней и осью Х сетки координат. Граничные случаи, когда рассматриваемая прямая параллельна осям координат, подтверждают вышенаписанное. Действительно для прямой, описанной уравнением y=const, угол между ней и осью абцисс равен нулю. Тангенс нулевого угла также равен нулю и угловой коэффициент тоже равен нулю.

Для прямых, перпендикулярных оси абцисс и описываемых уравнением х=const, угол между ними и осью Х равен 90 градусов. Тангенс прямого угла равен бесконечности, так же и угловой коэффициент подобных прямых равен бесконечности, что подтверждает написанное выше.

Угловой коэффициент касательной

Задача: Найти угловой коэффициент линии, касательной к функции y = 12x 2 + 2xe x при х = 0,1.

Решение: Найдем производную от исходной функции в общем виде

Ответ: Искомый угловой коэффициент в точке х = 0,1 равен 4,831

Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

Он лежит в пределах от 0 до 180 градусов.

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Наши точки имеют координаты (5;0) и (0;5). Значит,

Получили, что угловой коэффициент k = – 1.

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a b с осью оx.

В данном случае, проще использовать свойство подобия треугольников.

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

По условию точки имеют координаты (0;8) и (–12;0). Значит,

Получили, что угловой k = 2/3.

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки имеют координаты (0;0) и (10;24). Значит,

Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна –12.

Найдите ординату точки пересечения прямой, заданной уравнением

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у ). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината точки пересечения прямой с осью оу равна 3.

Найдите ординату точки пересечения прямых, заданных уравнениями

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем – х вместо у :

Ордината равна минус шести.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

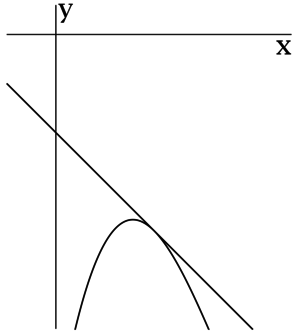
>> Угол наклона прямой от 0 до 90 градусов > Угол наклона прямой от 90 до 180 градусов

Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.

Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у). В обоих случаях необходимо брать производную функции.

В найденную производную подставьте координаты данной вам точки, чтобы вычислить угловой коэффициент. Производная функции равна угловому коэффициенту в определенной точке. Другими словами, f»(х) – это угловой коэффициент функции в любой точке (x,f(x)). В нашем примере:

Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.

Источник

Общая касательная к графикам функций. На примере 2х парабол

На примере двух парабол покажем, как составить уравнение общей касательной к графикам функций. Заметим, что общих касательных может быть несколько.

Для решения данной задачи потребуются знания о производной на уровне школьного курса.

В рамках подготовки к профильному ЕГЭ при изучении производной я предлагаю своим ученикам решать, в том числе, и подобные задачи, помимо стандартных 7 и 12 заданий.

Это необходимо для того, чтобы школьники учились применять свои знания при решении задач, а не просто решать стандартные задания по шаблону.

Составим уравнение общих касательных к графикам квадратичных функций (параболам):

Касательная представляет собой прямую. Запишем уравнение касательной в виде уравнения прямой с угловым коэффициентом:
y = kx + b, k – угловой коэффициент.
Обозначим точку, в которой она касается первой параболы, как A (a1, a2), второй параболы – B (b1, b2).

Рассмотрим функцию

1. Вычислим ее производную: y’ = 2(x – 1).

Таким образом, мы выразили координаты точки A через угловой коэффициент касательной:
A (k/2 + 1, k^2/4 + 1).

3. Угловой коэффициент прямой, проходящей через точки A (a1, a2) и B (b1, b2), равен (a2 – b2) / (a1 – b1). Значит
k = (a2 – b2) / (a1 – b1).

Подставим в это уравнение координаты точек A и B и получим уравнение относительно k:

Находим корни: k = 0 и k = 4.

5. Составляем уравнение касательной (прямой) по двум точкам. (Данная тема разобрана в предыдущем посте)
(x – a1) / (b1 – a1) = (y – a2) / (b2 – a2)
(x – 3) / (1 – 3) = (y – 5) / (-3 – 5)
(x – 3) / (–2) = (y – 5) / (-8) – каноническое уравнение прямой
Выражаем y:
y = 4x – 7 – уравнение прямой с угловым коэффициентом.

Аналогично находим уравнение еще одной касательной (при k = 0):
y = 1.

✔ Для того, чтобы задать вопрос или записаться на консультацию, пишите в whatsapp 8 968 814 30 80.

Источник