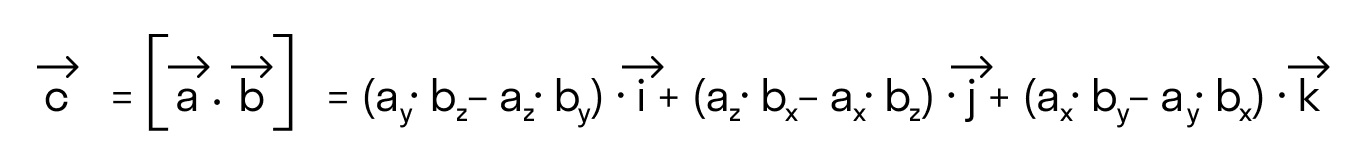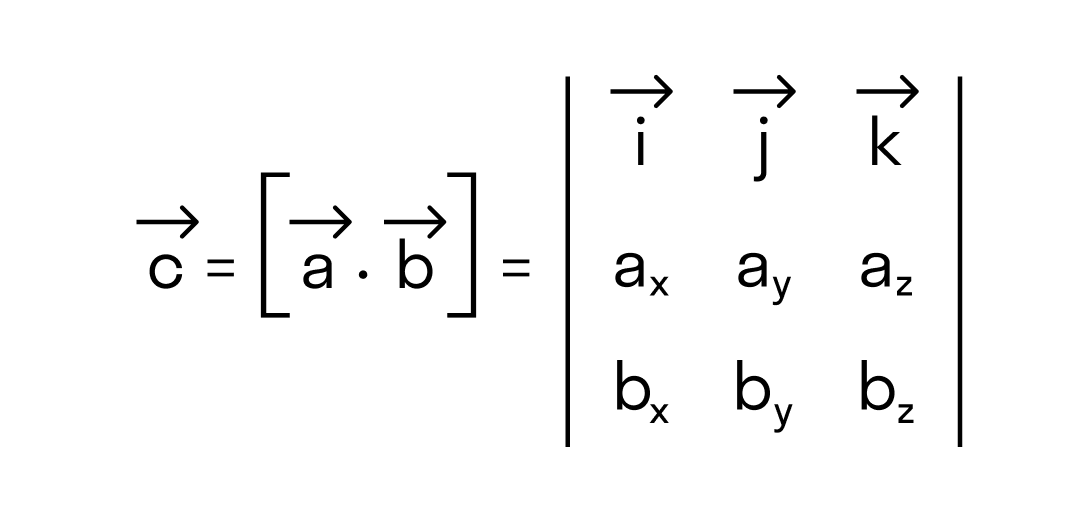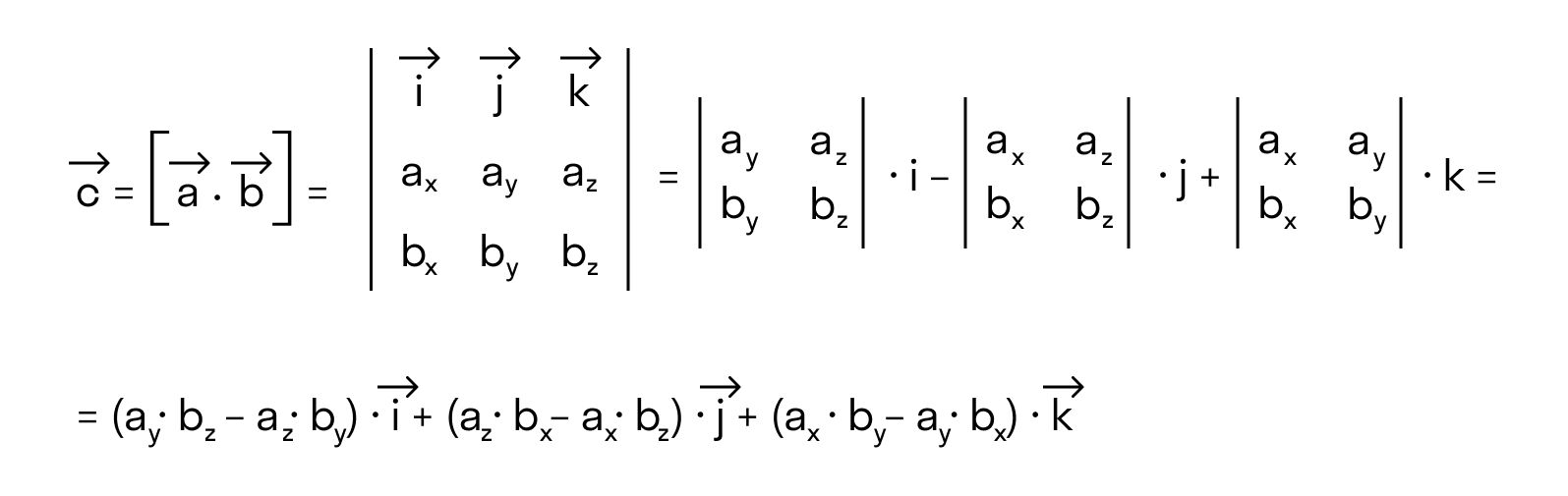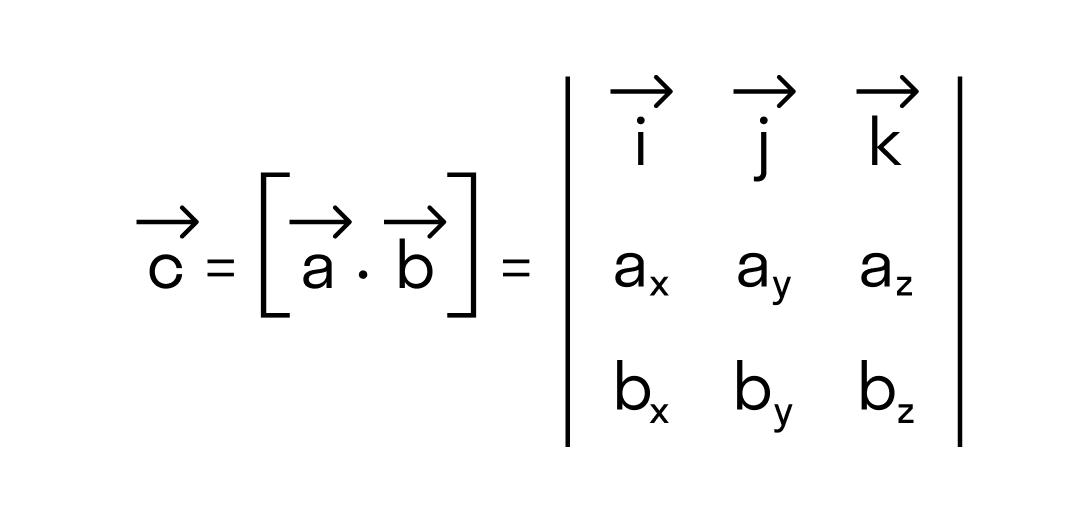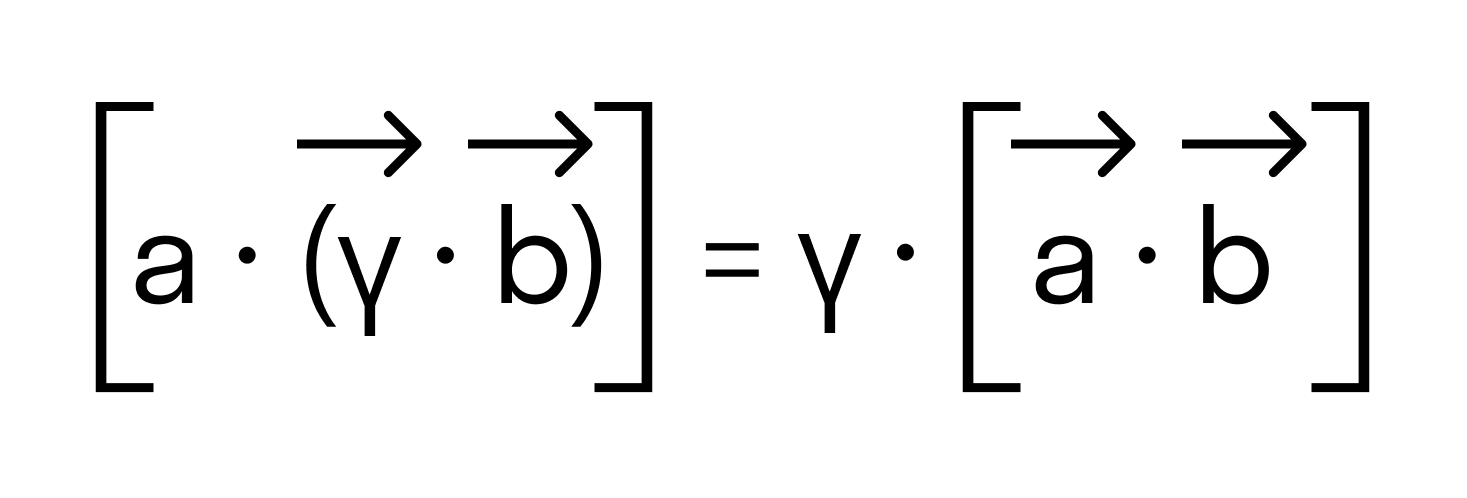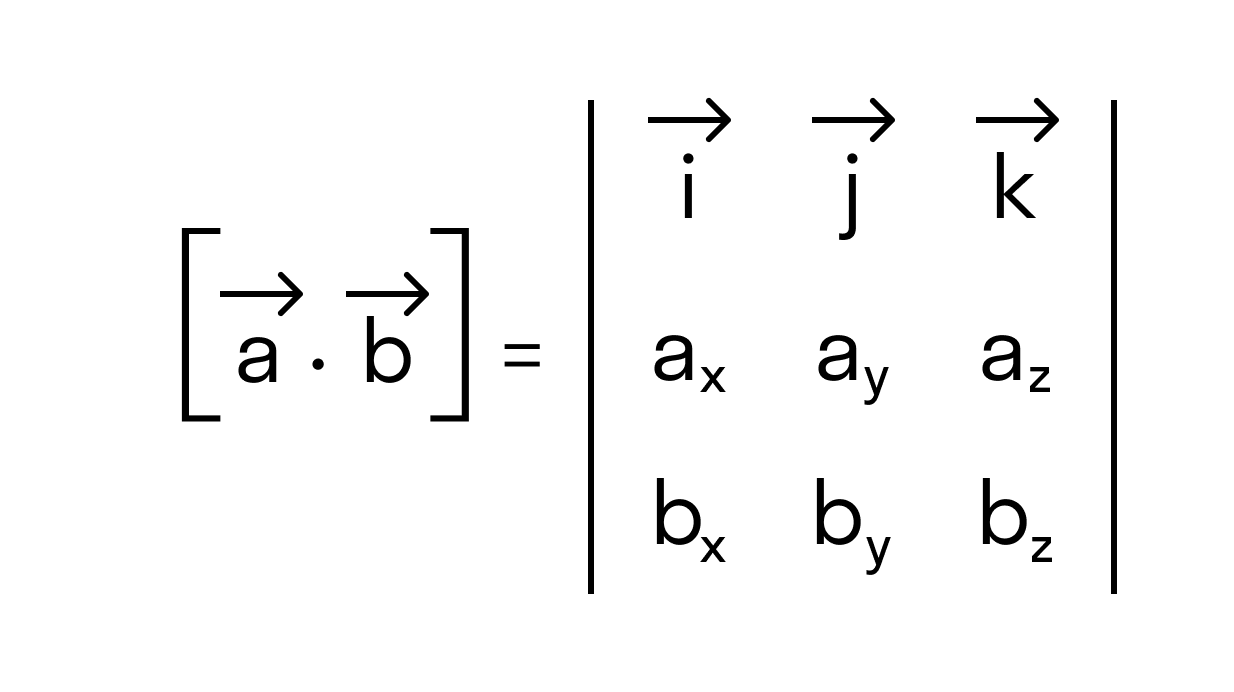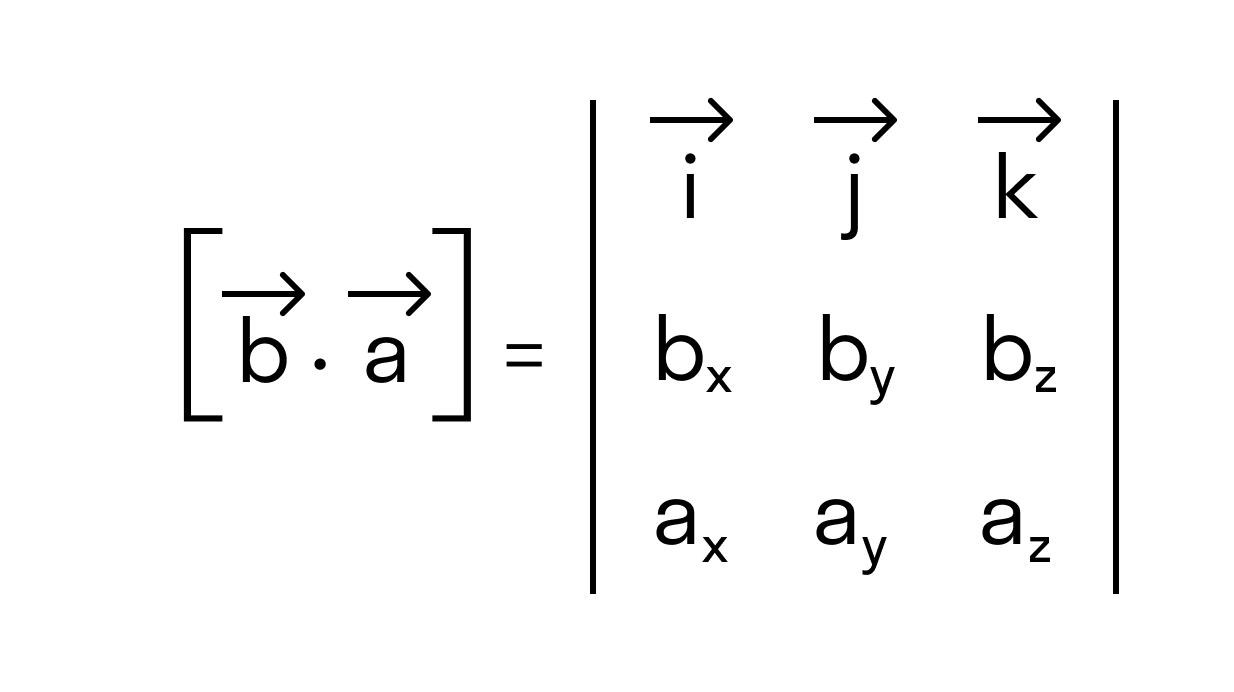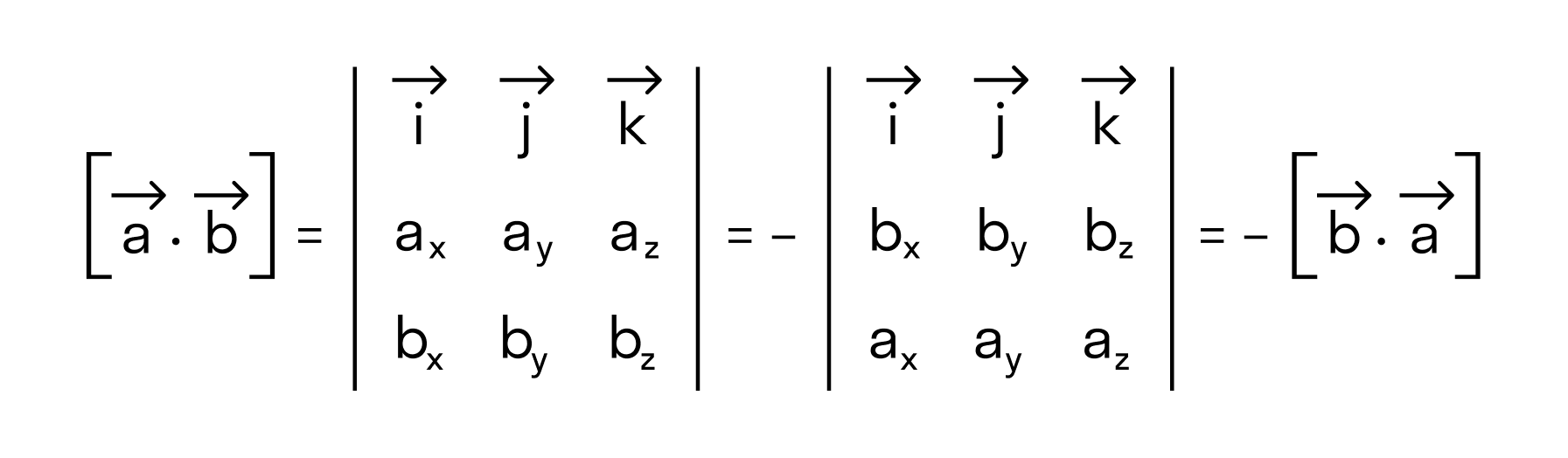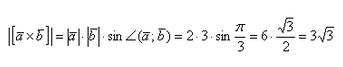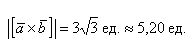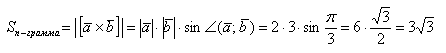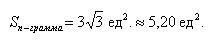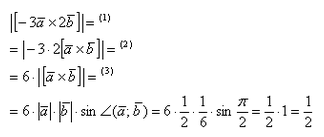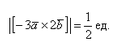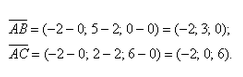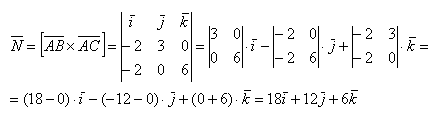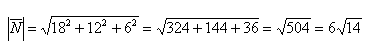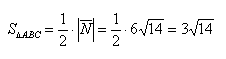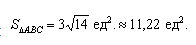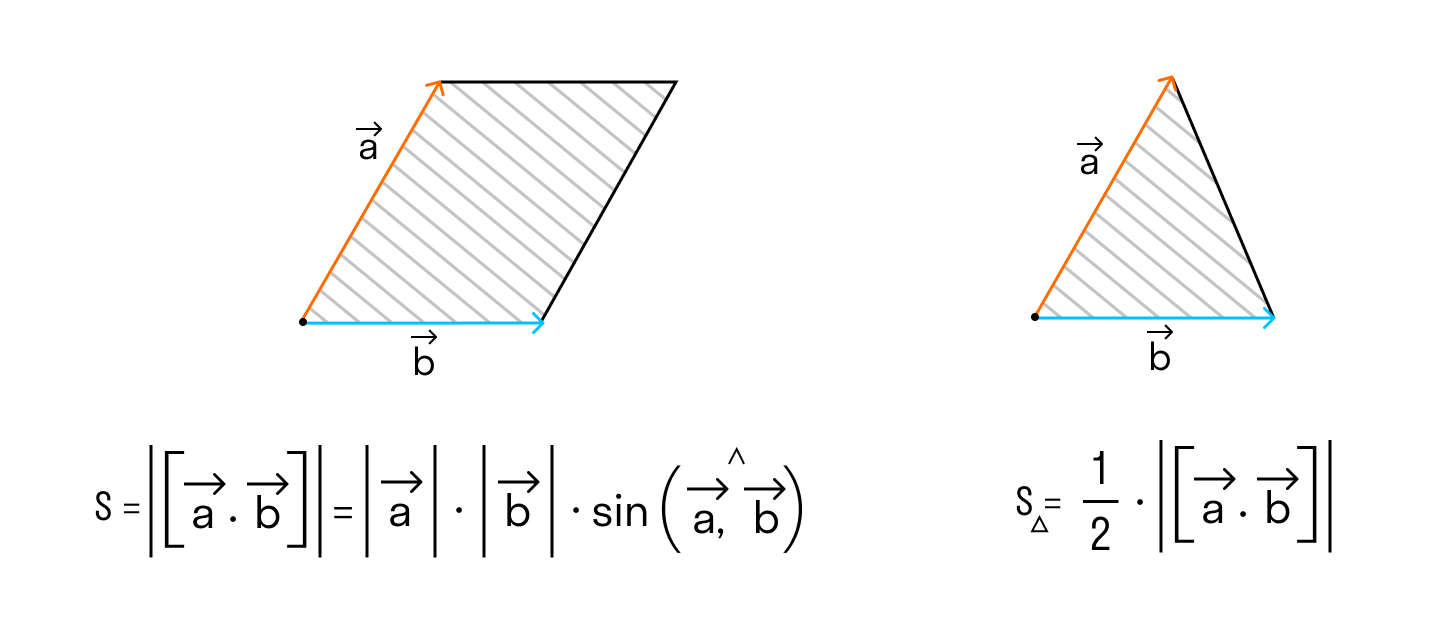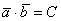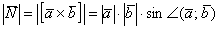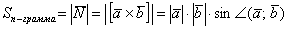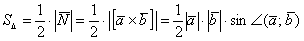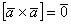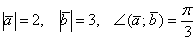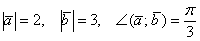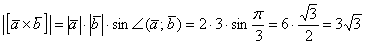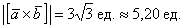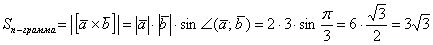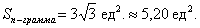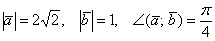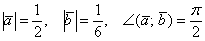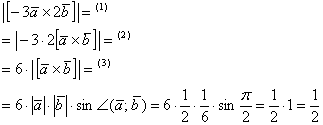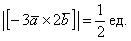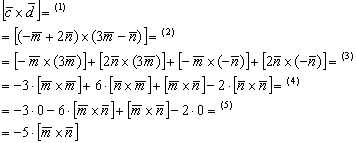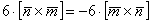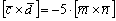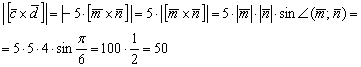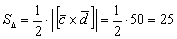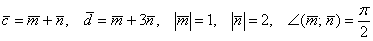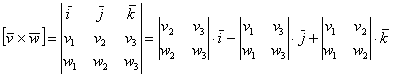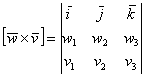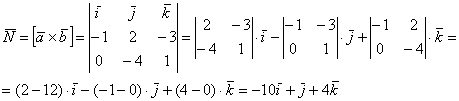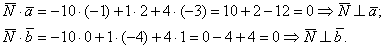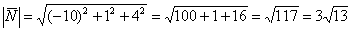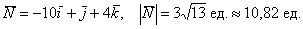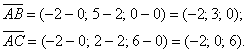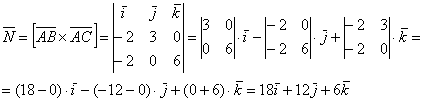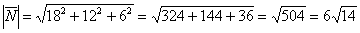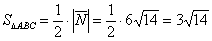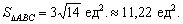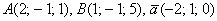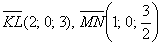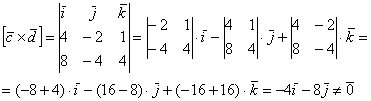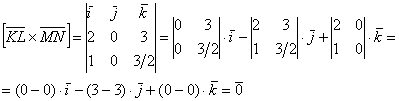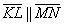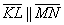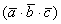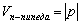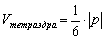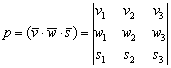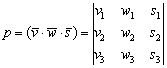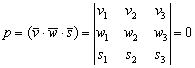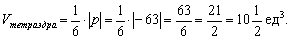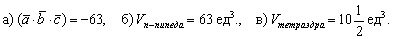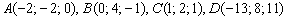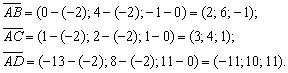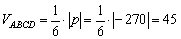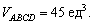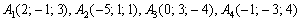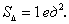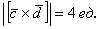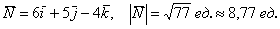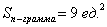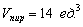Как искать векторное произведение векторов
Векторное произведение векторов
В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.
Геометрическая интерпретация
Формула векторного произведения
Произведение векторов a =
Свойства векторного произведения
1. Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.
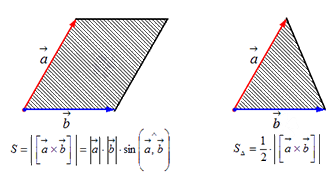
2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.
3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.
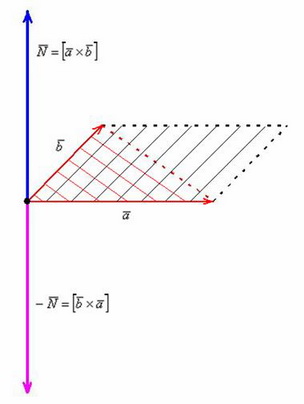
4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.
Пример задачи
Решение:
Определение векторного произведения
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Свойства векторного произведения
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) .
Рассмотрим следующие примеры.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Геометрический смысл векторного произведения
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Векторное произведение векторов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
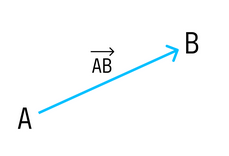
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
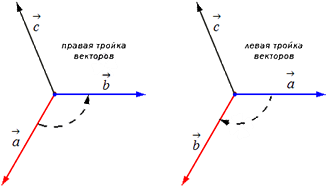
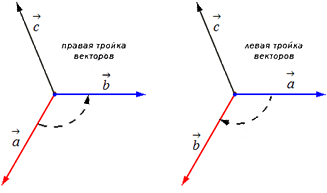
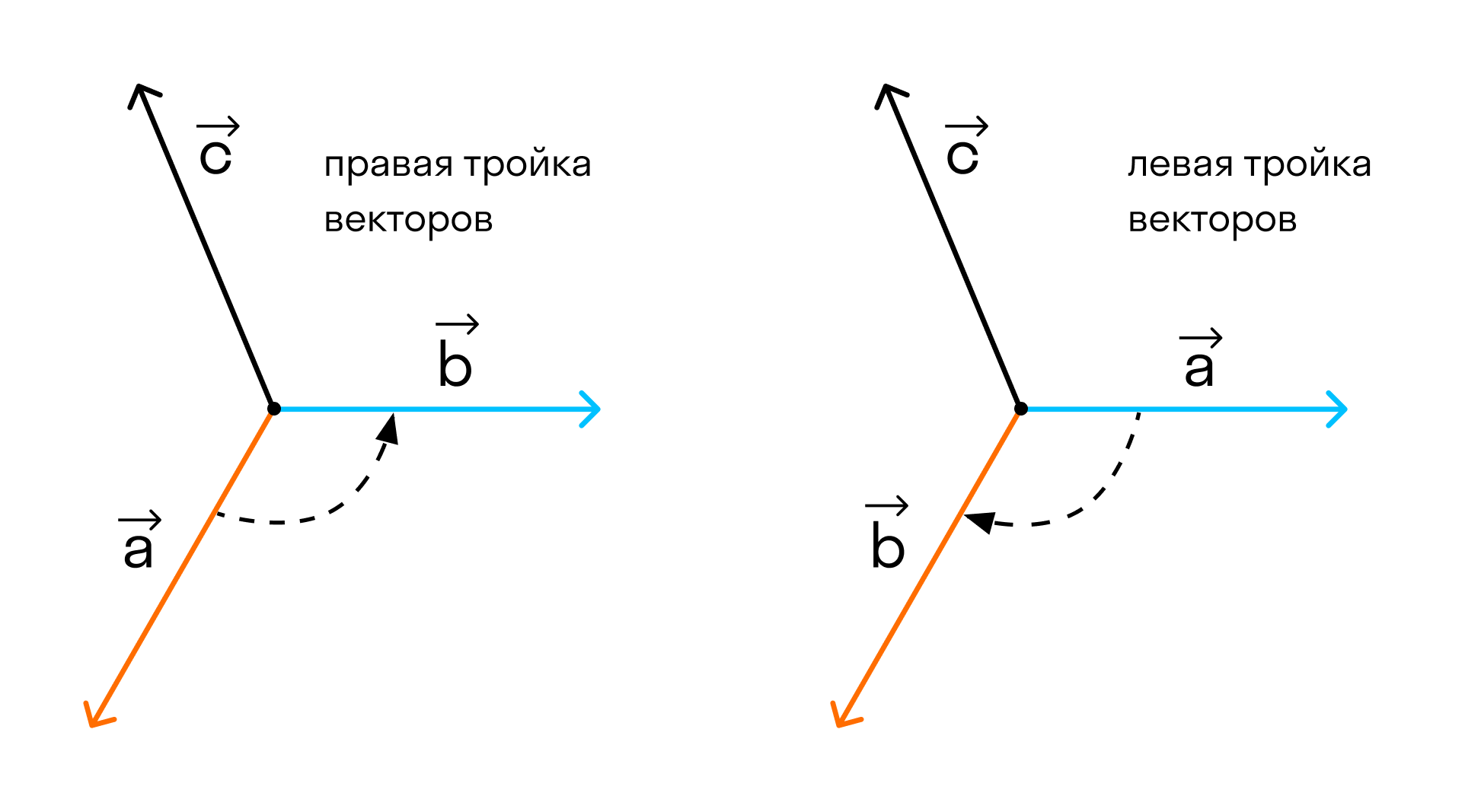
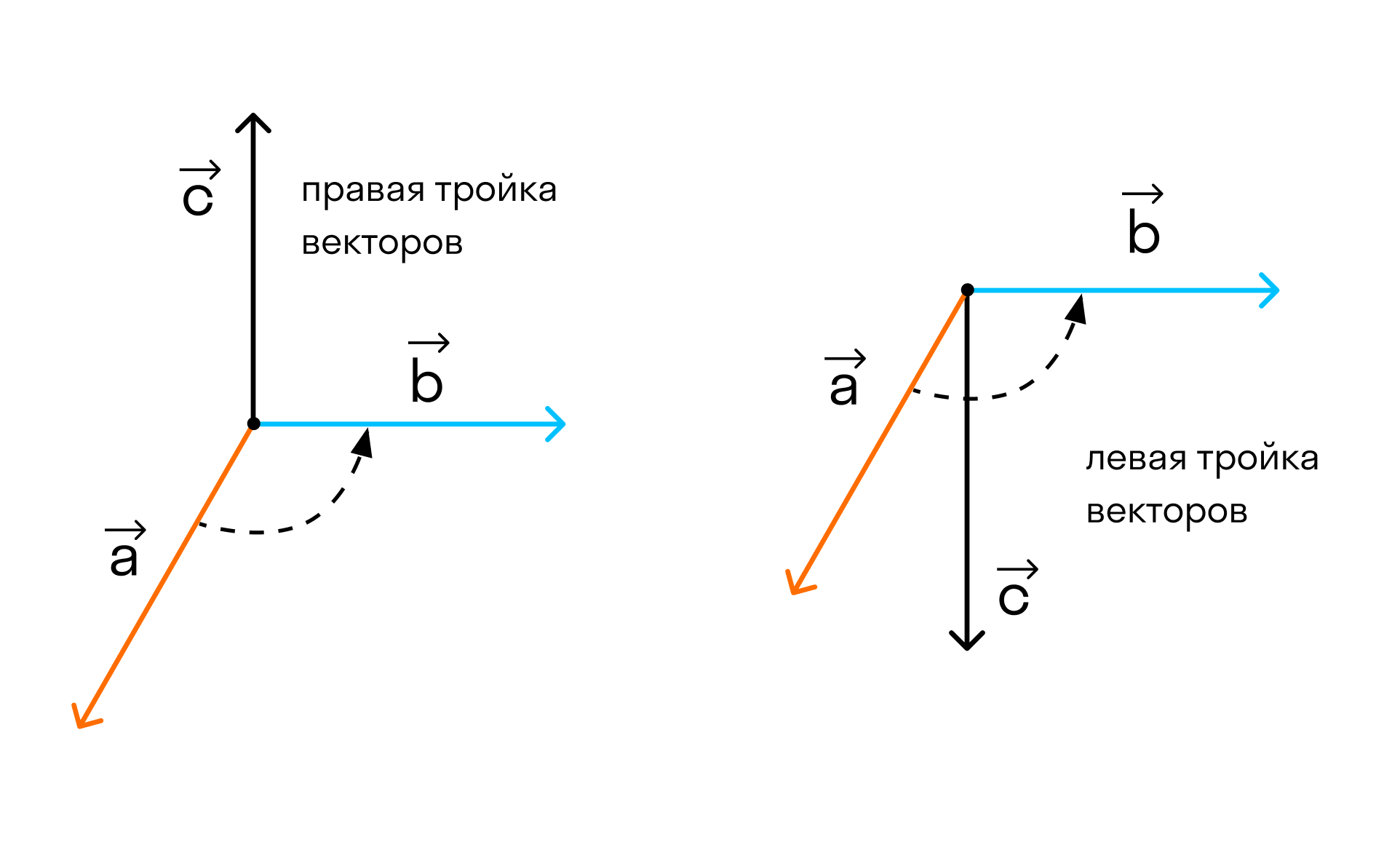
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
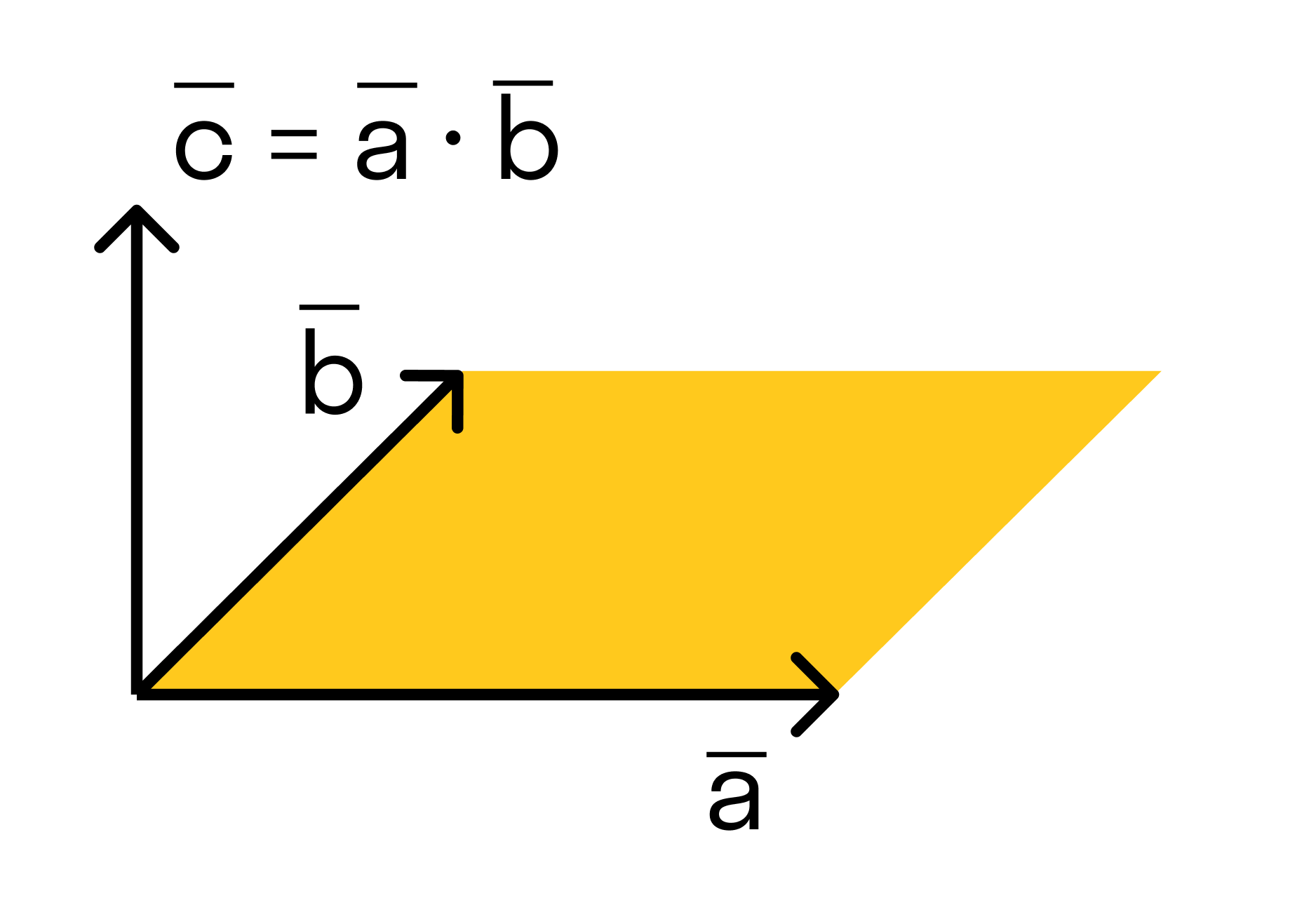
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a =
Векторное произведение векторов →a и →b обозначается как [→a • →b].
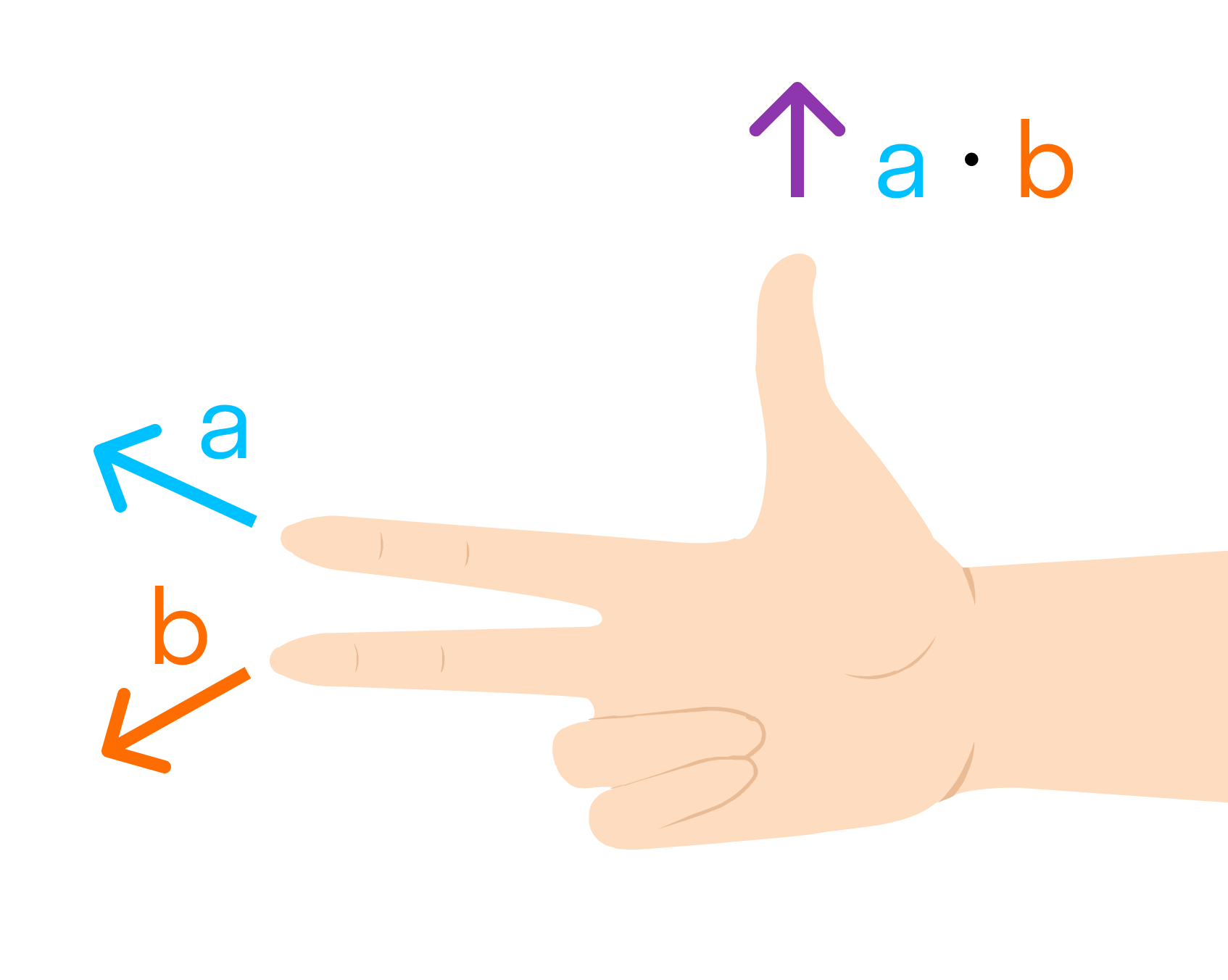
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
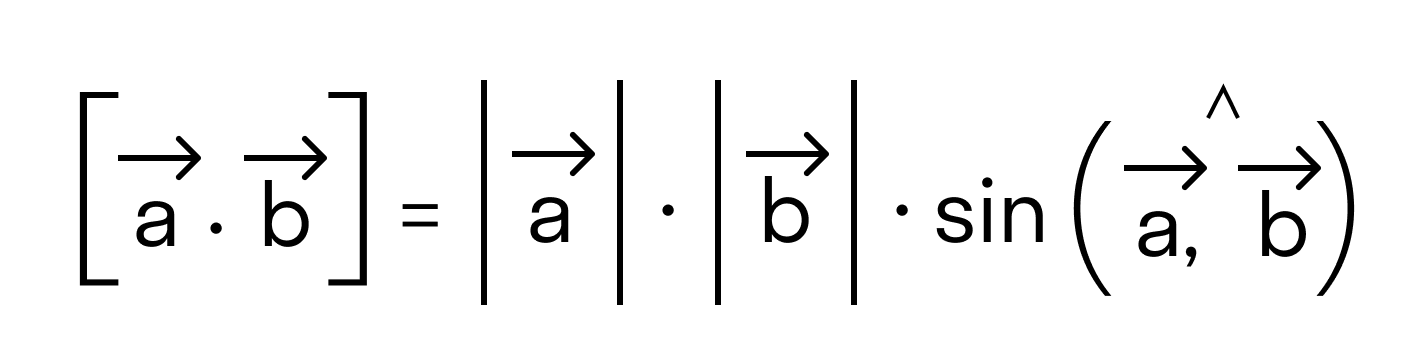
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
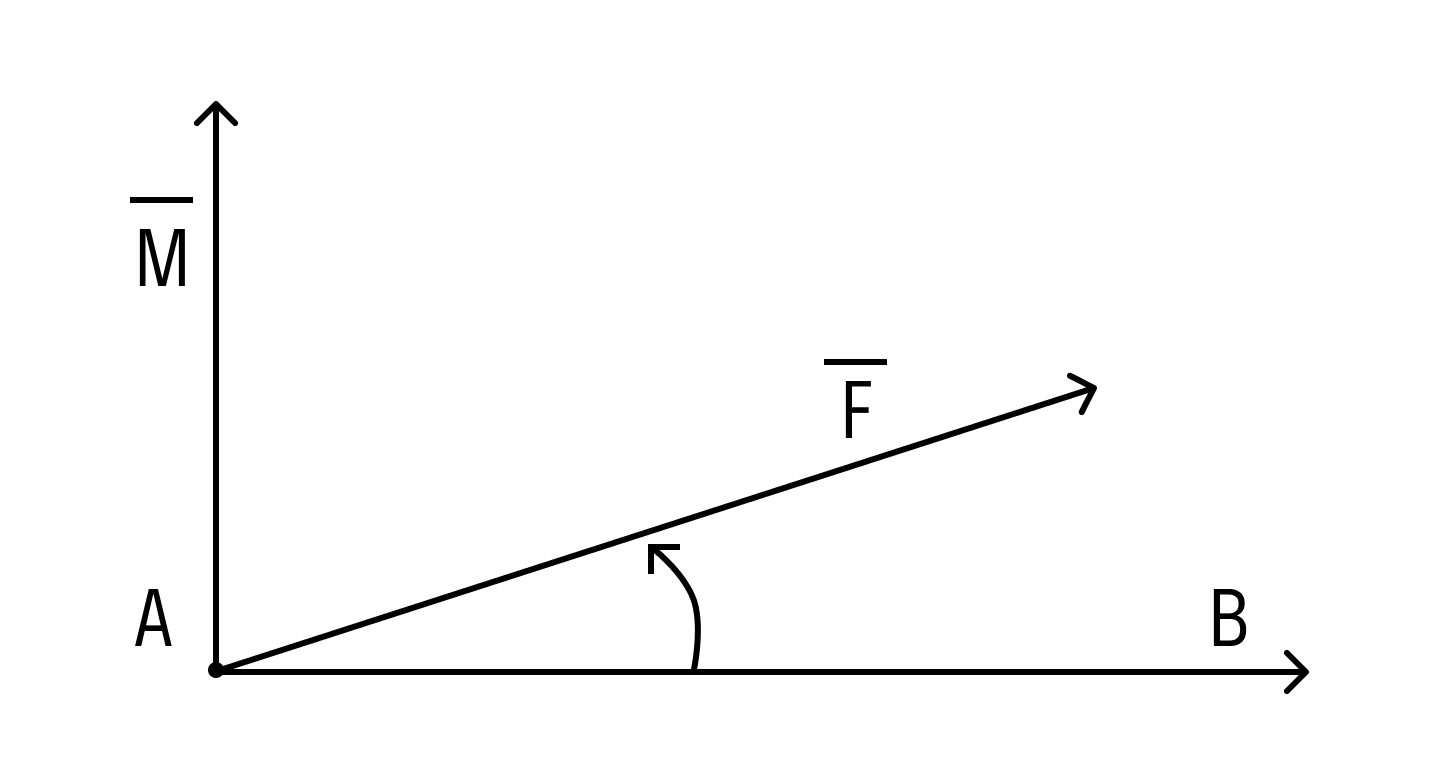
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно). Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Векторное произведение векторов
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора. Пусть это будут нетленные буквы 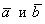
Само действие обозначается следующим образом: 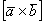
И сразу вопрос: если в скалярном произведении векторов 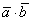
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР: 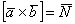
Определение векторного произведения
Сначала будет определение с картинкой, затем комментарии.
Определение: Векторным произведением 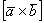
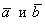
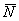
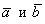
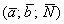
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы 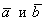
2) Векторы 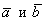
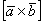
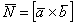
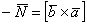
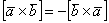
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора 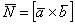
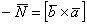
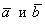
Примечание: чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе 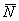
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах 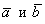
4) Не менее важный факт состоит в том, что вектор 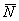
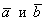
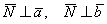
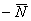
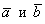
5) Вектор 
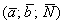
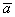
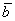
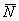
Теперь совместите указательный палец левой руки с тем же вектором 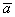
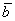
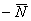
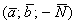
Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение 😉 Или просто попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются.
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторов
Определение подробно разобрано, осталось выяснить, что происходит, когда векторы 
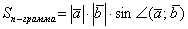
Таким образом, если 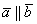
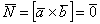
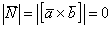
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица, чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
а) Найти длину векторного произведения векторов 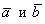
б) Найти площадь параллелограмма, построенного на векторах 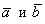
Решение: Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ:
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах 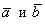
Ответ:
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что 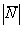
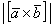
Популярный пример для самостоятельного решения:
Найти площадь треугольника, построенного на векторах 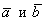
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторов
Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов 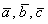
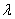
1) 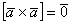
2) 
3) 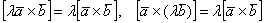
4) 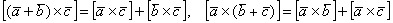
В качестве демонстрации рассмотрим коротенький пример:
Найти 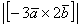
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ:
Пора подбросить дров в огонь:
Вычислить площадь треугольника, построенного на векторах 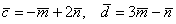
Решение: Площадь треугольника найдём по формуле 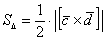
1) На первом шаге выразим векторное произведение 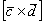
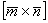
(1) Подставляем выражения векторов 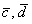
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству 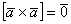
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ:
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Найти 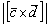
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров 😉
Векторное произведение векторов в координатах
С векторами, заданными в координатах, всё тоже просто и прозрачно. Сразу обращаю внимание на то, что разговор пойдёт о координатах ортонормированного базиса. В общем случае аффинного базиса нижеприведённая формула будет нерабочей. Кстати, кто ещё не успел ознакомиться с базисами, рекомендую статью Линейная (не) зависимость векторов. Базис векторов.
Векторное произведение векторов 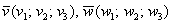
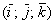
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов 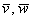
Согласно свойствам определителя, если в определителе две строки переставить местами, то он сменит знак. Этот факт полностью соответствует свойству антикоммутативности векторного произведения.
Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Если есть трудности с определителями и формула не очень понятна, пожалуйста, посетите урок Как вычислить определитель, всё станет на свои места.
Что получается в результате раскрытия определителя?
В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.
Найти векторное произведение векторов 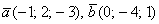
Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), и во-вторых, его длину.
1) Найдём векторное произведение:
В результате получен вектор 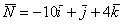
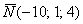
Существует очень хороший способ проверки: как следует из определения, вектор 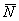
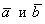
Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.
2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора, которая рассматривалась на уроке Векторы для чайников:
Ответ:
В плане технических обозначений здесь, наоборот, вместо громоздкой конструкции 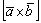
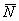
Аналогичный пример для самостоятельного решения:
Даны векторы 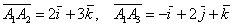
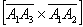
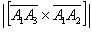
Решение с ответом в конце урока. Будьте внимательны!
Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:
Даны вершины треугольника 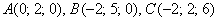
Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:
Ответ:
Рассмотренную задачу можно решить ещё двумя способами – было не обязательно выбирать стороны 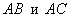
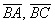
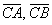
Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить 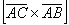
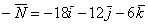
Вычислить площадь параллелограмма, построенного на векторах 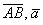
Это пример для самостоятельного решения.
В заключение первого раздела рассмотрим обещанную задачу урока Линейная (не) зависимость векторов. Базис векторов:
Проверить, будут ли коллинеарны следующие векторы пространства:
а) 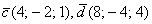
б)
Решение: Проверка основана на одном из утверждений данного урока: если векторы 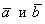
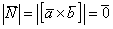
а) Найдём векторное произведение:
Таким образом, векторы 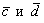
б) Найдём векторное произведение:
Значит,
Ответ: а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Смешанное произведение векторов
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов:
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение: Смешанным произведением 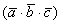
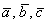
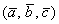
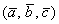
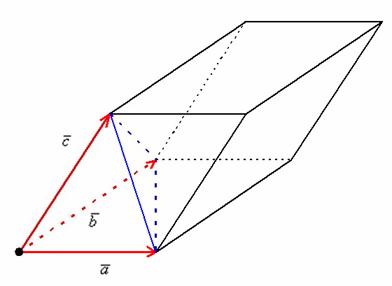
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
1) Исходные векторы 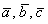
С компланарными векторами разберёмся ниже (что такое компланарность векторов, подробно разъяснено в статье Линейная (не) зависимость векторов. Базис векторов).
2) Векторы 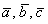
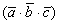
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ: 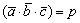
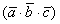
По определению смешанное произведение – это объем параллелепипеда, построенного на векторах 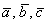
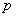
Примечание: чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму 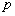
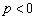
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах 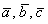
Знак модуля уничтожает возможный «минус» смешанного произведения.
В курсе аналитической геометрии доказано, что объём тетраэдра (на рисунке отсечён «синей» плоскостью) равен одной шестой объёма параллелепипеда:
В теории и практике тетраэдр часто называют треугольной пирамидой, поскольку все грани тетраэдра – треугольники.
Смешанное произведение компланарных векторов
Если векторы 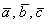
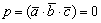
Немного отвлекусь от темы, возможно, не все знают ответы на следующие вопросы:
– Чему равны длина и ширина точки?
– Чему равна площадь прямой?
– Чему равен объём плоскости?
С позиции геометрии ответ таков: нулю
Смешанное произведение векторов в координатах
Способ расчёта смешанного произведения векторов чисто алгебраический:
Смешанное произведение векторов 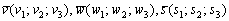
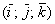
Определение, строго говоря, неполное, но в теоретические тонкости вникать не будем, правая ориентация базиса – это его «нормальная» ориентация, в которой мы будем решать практические задачи. Вполне достаточно.
В различных источниках на ваши головы выльют тонны различных свойств смешанного произведения. С практической точки зрения считаю важным отметить лишь некоторые вещи:
Как и для векторного произведения, координаты векторов следует «укладывать» в определитель в строгом порядке. Если в смешанном произведении 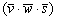
Следует отметить, что координаты векторов не обязательно записывать в строки, их можно записать и в столбцы – слева направо, и тоже в строгом порядке:
Значение определителя от этого не изменится (см. статью Свойства определителя и понижение его порядка). Дело вкуса.
Второй важный момент касается компланарности векторов. Как уже отмечалось, если векторы 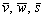
Такое задание уже было! В конце урока Линейная (не) зависимость векторов. Базис векторов мы разбирали задачу «доказать, что три вектора образуют базис пространства», где рассчитывали определитель третьего порядка и получали некоторое число. Так вот: по сути – мы находили смешанное произведение трёх векторов. И с геометрической точки зрения полученное число по модулю равнялось объёму параллелепипеда, построенного на данных векторах! Ну, а если получался ноль, то делали вывод, что векторы компланарны и базиса не образуют.
Закидываем остатки Буратино в огонь:
Даны векторы 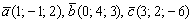
Вычислить:
а) смешанное произведение векторов;
б) объём параллелепипеда, построенного на векторах 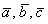
в) объём тетраэдра, построенного на векторах 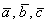
Решение: Всё быстро и просто:
а) По формуле смешанного произведения:
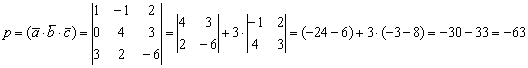
(Определитель раскрыт по первому столбцу)
б) Объём параллелепипеда, построенного на векторах 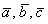
в) Вычислим объём тетраэдра, построенного на данных векторах:
Ответ:
В пункте а) тоже можно было добавить размерность «кубические единицы», но здесь к объёму добавляется знак «минус», поэтому смотреться будет всё-таки не очень.
На практике, по моей субъективной оценке, в 95-99% случаев требуется вычислить объём треугольной пирамиды:
Вычислить объём треугольной пирамиды, если даны её вершины
Решение: Чайникам рекомендую выполнить схематический рисунок пирамидки, чтобы лучше понять суть проводимых действий.
Сначала найдём векторы:
Вычислим смешанное произведение: 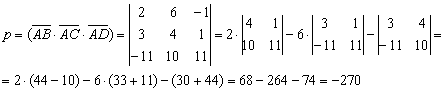
(Определитель раскрыт по первой строке)
Вычислим объём треугольной пирамиды 
Ответ:
Рассмотренная задача имеет не единственное решение, можно было взять и другую группу векторов, начиная движуху от любой другой вершины пирамиды. Чем-то похоже на задачу предыдущей части урока о площади треугольника.
Объём тетраэдра – хит смешанного произведения, поэтому заключительный счастливый номер пусть будет таким же:
Вычислить объём пирамиды, заданной вершинами
Это пример для самостоятельного решения. В образце решения рассмотрены векторы, отложенные от «традиционной» точки 
Остались только веселящие душу угольки, и в заключение хочу добавить, что в общем виде смешанное произведение векторов определено в аффинной системе координат. Более подробную информацию и формулы можно почерпнуть у тандема Атанасяна-Базылева.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: По соответствующей формуле: 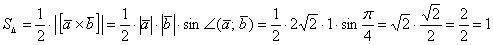
Ответ:
Пример 5: Решение:
1) Выразим вектор 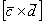
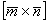
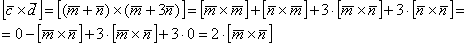
2) Вычислим длину векторного произведения: 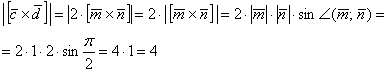
Ответ:
Пример 7: Решение: 1) Найдём векторное произведение: 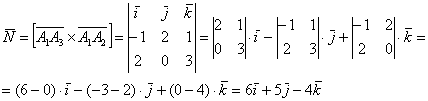
2) Вычислим длину векторного произведения: 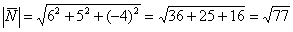
Ответ:
Пример 9: Решение: Найдём вектор: 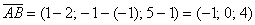
Векторное произведение: 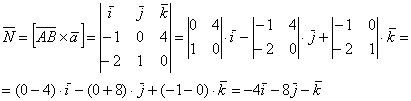
Площадь параллелограмма: 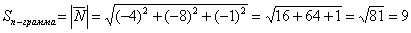
Ответ:
Пример 13: Решение: Найдём векторы: 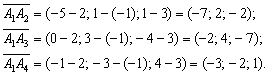
Вычислим смешанное произведение: 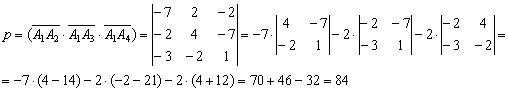
(Определитель раскрыт по первой строке)
Вычислим объём пирамиды 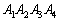
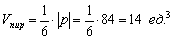
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5