Как измерить частоту периодического сигнала
Как измерить частоту периодического сигнала
Реальные сигналы не идеальны, они никогда не бывают строго периодическими. Тем не менее, по отношению к реальным сигналам также используется понятие частоты. Что понимают под частотой в этом случае?
Введение
Понятие частоты периодического сигнала
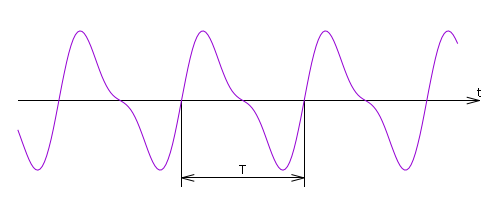
Рис. %img:pf
* В математике также рассматриваются «почти периодические» функции, но это весьма специфический вопрос и в математике этим термином обозначается не совсем то, что имеется в виду под «почти периодическими» функциями в технике.
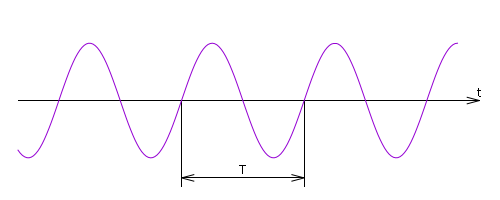
Рис. %img:hf
Частота реального сигнала. Мгновенная частота
Строгие определения и формальные теоретические подходы хороши для математики. В реальной жизни, в технике, сигналы никогда не бывают периодическими. Прежде всего, потому что никакой сигнал не может длиться бесконечно долго. Сигнал имеет начало и конец, что уже нарушает идеальную периодичность. Но даже если отвлечься от этого, скорее философского вопроса о конечности существования, то и за время существования сигнала, строгая периодичность недостижима. С другой стороны, некоторая степень регулярности и повторяемости характерна для очень многих реальных сигналов.
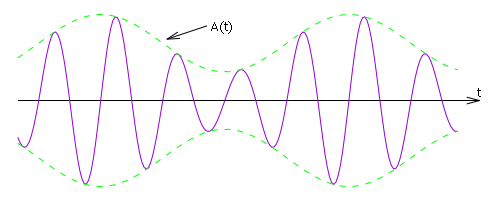
Рис. %img:cf
Заметим, что даже в случае периодических с математической точки зрения, идеальных сигналов, иногда бывает удобнее рассматривать их как «не вполне» периодические, с изменяющейся во времени амплитудой и/или частотой.
Очевидно, что период \( T = 2 \pi / \omega \) несущего колебания уже не является периодом модулированного сигнала из-за множителя \( (1 + m \sin \Omega t) \), который изменится через время T.
Излишне говорить, что с практической точки зрения такой подход совершенно неудобен; истинные частота и период рассмотренного сигнала абсолютно не отражают его реальных свойств. В то же время, мгновенная частота, которая в случае амплитудно-модулированного сигнала равна частоте несущего сигнала \( \omega \), оказывается намного более объективной и информативной характеристикой сигнала.
Очень точному измерению поддаётся среднее значение частоты сигнала, об этом далее.
Среднее значение частоты. Измерение частоты
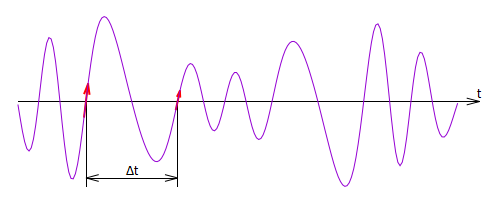
Рис. %img:mf
Получили что для того, чтобы измерить среднее значение частоты, достаточно измерить промежуток времени между двумя моментами, когда сигнал проходит через нулевое значение (в одном направлении). Впрочем, этот результат вполне соответствует интуитивному представлению о периоде реального сигнала и соотношению между периодом и частотой.
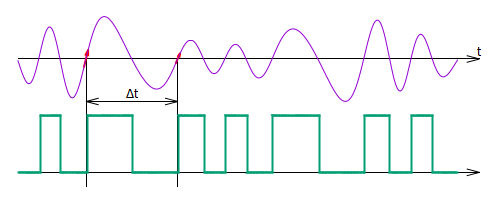
Рис. %img:df
На самом деле, обязательно наличие гистерезиса при преобразовании (порог переключения от 0 к 1 должен быть выше, чем порог обратного переключения). В противном случае, вблизи порога переключения будем получать пачки паразитных импульсов из-за наличия шумов и помех в сигнале. Но это детали реализации, не изменяющие самого принципа.
Динамическая погрешность измерений
Мы нашли способ определения средней частоты сигнала за некоторый интервал времени с высокой точностью. Но если частота сигнала изменяется, средняя частота даёт слишком мало информации о сигнале. Зачастую бывает необходимо знать, как во времени изменяется мгновенная частота сигнала и насколько сильно она отклоняется от среднего значения.
Заметим, что если частота изменяется не по гармоническому закону, всё равно, мгновенную частоту как функцию можно разложить на гармонические составляющие и рассматривать воздействие операции усреднения на каждую составляющую по отдельности. Это возможно, поскольку операция усреднения является линейной.
На основе полученных выводов можем должным образом выбрать интервал измерения.
Если идёт речь о достижении как можно более высокой точности в измерении мгновенной частоты, то следует далее уменьшать интервал измерения. С уменьшением интервала, результат всё более приближается к мгновенной частоте, т.е. уменьшается динамическая погрешность измерения, но одновременно с этим растёт погрешность метода. Это ограничивает предельную точность измерения частоты путём измерения средней частоты сигнала. Не имеет смысла снижать абсолютную динамическую погрешность \( <\Delta>_2 \) до значений меньше абсолютной погрешности метода \( \Delta_1 \).
Пример. Сигнал имеет среднюю частоту f0 = 100 кГц, мгновенная частота отклоняется от среднего значения на величину \( \Delta f = 1 \text < Гц>\), причём отклонение описывается синусоидой с частотой F = 10 Гц. Требуется определить оптимальный интервал измерения (при котором погрешность метода достигает динамической погрешности измерения), если частота опорного генератора составляет fr = 24 МГц. Вычисления по приведённой выше формуле дают результат \( \Delta t \approx 0.03\text < с>\) (абсолютная погрешность метода измерения и динамическая погрешность при этом оказываются порядка 0.14 Гц).
Другим простым, но представляющим интерес примером, является измерение средней частоты сигнала, мгновенная частота которого на некотором интервале изменяется линейно. Легко показать (настолько легко, что подробно не будем на этом останавливаться), что результат будет равен мгновенной частоте в момент, соответствующий середине интервала измерения, или, что то же самое, среднему арифметическому мгновенных частот на концах интервала измерения.
Литература
Особенно хотелось бы отметить книгу «Сигналы, помехи, ошибки. «. Это замечательная книга, в которой хорошо раскрывается понятие мгновенной частоты; поясняется, в каких случаях уместно говорить о частоте сигнала, а когда следует переходить к рассмотрению спектра, а также подробно обсуждаются многие другие вопросы. Материал излагается довольно живо, доступно, но не упрощённо. И что приятно, книга не лишена тонкого ненавязчивого юмора.
В математических энциклопедиях можно найти определения базовых понятий (периодическая функция; почти периодическая функция; период; частота).
В энциклопедии по физике также можно найти аналогичные определения периодичности, периода, частоты и т.д.
Проведение измерений с помощью осциллографа
Именно она делает цифровой осциллограф недоступным для любительских целей, хотя существуют «карманные» осциллографы стоимостью всего в несколько тысяч рублей, которые продаются на Алиэкспресс, но пользоваться ими не особенно удобно. Ну, просто интересная игрушка. Поэтому пока речь пойдет об измерениях с помощью электронного осциллографа.
На тему выбора осциллографа для использования в домашней лаборатории в интернете можно найти достаточное количество форумов. Не отрицая достоинств цифровых осциллографов, на многих форумах советуют остановить выбор на простых малогабаритных и надежных осциллографах отечественной разработки С1-73 и С1-101 и подобных, с которыми мы ранее познакомились в этой статье.
При достаточно демократичной цене эти приборы позволят выполнить большинство радиолюбительских задач. А пока познакомимся с общими принципами измерений с помощью осциллографа.
Рисунок 1. Осциллограф С1-73
Что измеряет осциллограф
Измеряемый сигнал подается на вход канала вертикального отклонения Y, который имеет большое входное сопротивление, как правило, 1MΩ, и малую входную емкость, не более 40pF, что позволяет вносить минимальные искажения в измеряемый сигнал. Эти параметры часто указываются рядом с входом канала вертикального отклонения.
Рисунок 2. Осциллограф С1-101
Высокое входное сопротивление свойственно вольтметрам, поэтому можно с уверенностью сказать, что осциллограф измеряет напряжение. Применение внешних входных делителей позволяет снизить входную емкость и увеличить входное сопротивление. Это также снижает влияние осциллографа на исследуемый сигнал.
Здесь следует вспомнить, что существуют специальные высокочастотные осциллографы, входное сопротивление которых всего 50 Ом. В радиолюбительской практике такие приборы не находят применения. Поэтому далее речь пойдет об обычных универсальных осциллографах.
Полоса пропускания канала Y
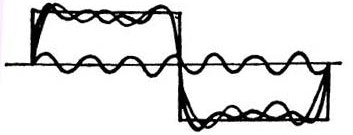
При этом следует иметь в виду, что полоса пропускания канала вертикального отклонения Y д.б. не менее, чем в 5 раз выше частоты сигнала, который будет измеряться. То есть усилитель вертикального отклонения должен пропускать не ниже пятой гармоники исследуемого сигнала. Особенно это требуется при исследовании прямоугольных импульсов, которые содержат множество гармоник, как показано на рисунке 3. Только в этом случае на экране получается изображение с минимальными искажениями.
Рисунок 3. Синтез прямоугольного сигнала из гармонических составляющих
Кроме основной частоты на рисунке 3 показаны третья и седьмая гармоники. С увеличением номера гармоники возрастает ее частота: частота третьей гармоники в три раза выше основной, пятой гармоники в пять раз, седьмой в семь и т.д. Соответственно амплитуда высших гармоник падает: чем выше номер гармоники, тем ниже ее амплитуда. Только если усилитель вертикального канала без особого ослабления сможет пропустить высшие гармоники, изображение импульса получится прямоугольным.
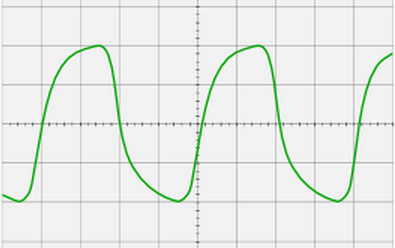
На рисунке 4 показана осциллограмма меандра при недостаточной полосе пропускания канала Y.
Примерно так выглядит меандр частотой 500 КГц на экране осциллографа ОМШ-3М с полосой пропускания 0…25 КГц. Как будто прямоугольные импульсы пропущены через интегрирующую RC цепочку. Такой осциллограф выпускался советской промышленностью для лабораторных работ на уроках физики в школах. Даже напряжение питания этого прибора в целях безопасности было не 220, а всего 42В. Совершенно очевидно, что осциллограф с такой полосой пропускания позволит почти без искажений наблюдать сигнал с частотами не более 5КГц.
У обычного универсального осциллографа полоса пропускания чаще всего составляет 5 МГц. Даже при такой полосе можно увидеть сигнал до 10 МГц и выше, но полученное на экране изображение позволяет судить лишь о наличии или отсутствии этого сигнала. О его форме что-либо сказать будет затруднительно, но в некоторых ситуациях форма не столь уж и важна: например есть генератор синусоиды, и достаточно просто убедиться, есть эта синусоида или ее нет. Как раз такая ситуация показана на рисунке 4.
Современные вычислительные системы и линии связи работают на очень высоких частотах, порядка сотен мегагерц. Чтобы увидеть столь высокочастотные сигналы полоса пропускания осциллографа должна быть не менее 500 МГц. Такая широкая полоса очень «расширяет» цену осциллографа.
В качестве примера можно привести цифровой осциллограф U1610A показанный не рисунке 5. Его полоса пропускания 100МГц, при этом цена составляет почти 200 000 рублей. Согласитесь, не каждый может позволить себе купить столь дорогой прибор.
Пусть читатель не сочтет этот рисунок за рекламу, поскольку все координаты продавца не закрашены: на месте этого рисунка мог оказаться любой подобный скриншот.
Виды исследуемых сигналов и их параметры
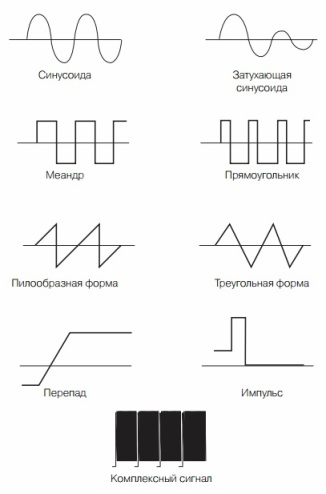
Наиболее распространенным видом колебаний в природе и технике является синусоида. Это та самая многострадальная функция Y=sinX, которую проходили в школе на уроках тригонометрии. Достаточно много электрических и механических процессов имеют синусоидальную форму, хотя достаточно часто в электронной технике применяются и другие формы сигналов. Некоторые из них показаны на рисунке 6.
Рисунок 6. Формы электрических колебаний
Периодические сигналы. Характеристики сигналов
Универсальный электронный осциллограф позволяет достаточно точно исследовать периодические сигналы. Если же на вход Y подать реальный звуковой сигнал, например, музыкальную фонограмму, то на экране будут видны хаотично мелькающие всплески. Естественно, что детально исследовать такой сигнал невозможно. В этом случае поможет применение цифрового запоминающего осциллографа, который позволяет сохранить осциллограмму.
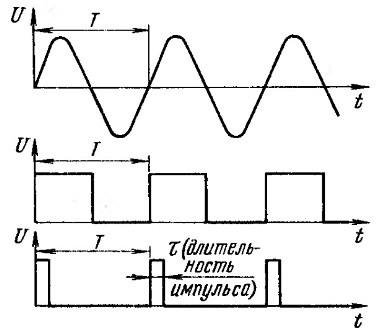
Колебания, показанные на рисунке 6, являются периодическими, повторяются, через определенный период времени T. Подробнее это можно рассмотреть на рисунке 7.
Рисунок 7. Периодические колебания
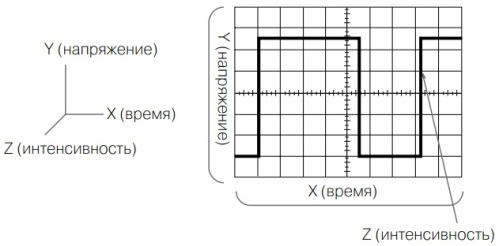
Колебания изображены в двухмерной системе координат: по оси ординат отсчитывается напряжение, а по оси абсцисс время. Напряжение измеряется в вольтах, время в секундах. Для электрических колебаний время чаще измеряется в миллисекундах или микросекундах.
Кроме компонентов X и Y осциллограмма содержит еще компонент Z – интенсивность, или попросту яркость (рисунок 8). Именно она включает луч на время прямого хода луча и гасит на время обратного хода. Некоторые осциллографы имеют вход для управления яркостью, который так и называется вход Z. Если на этот вход подать импульсное напряжение от образцового генератора, то на экране можно увидеть частотные метки. Это позволяет точнее отсчитывать длительность сигнала по оси X.
Рисунок 8. Три компонента исследуемого сигнала
Современные осциллографы имеют, как правило, калиброванные по времени развертки, позволяющие точно отсчитывать время. Поэтому пользоваться внешним генератором для создания меток практически не приходится.
В верхней части рисунка 7 располагается синусоида. Нетрудно видеть, что начинается она в начале координатной системы. За время T (период) выполняется одно полное колебание. Далее все повторяется, идет следующий период. Такие сигналы называются периодическими.
Ниже синусоиды показаны прямоугольные сигналы: меандр и прямоугольный импульс. Они также периодические с периодом T. Длительность импульса обозначена как τ (тау). В случае меандра длительность импульса τ равна длительности паузы между импульсами, как раз половина периода T. Поэтому меандр является частным случаем прямоугольного сигнала.
Скважность и коэффициент заполнения
В англоязычной терминологии как раз все наоборот. Там импульсы характеризуются коэффициентом заполнения, соотношением длительности импульса к периоду следования Duty cycle: D=τ/T. Коэффициент заполнения выражается в %%. Таким образом, для меандра D=50%. Получается, что D=1/S, коэффициент заполнения и скважность величины взаимно обратные, хотя характеризуют собой один и тот же параметр импульса. Осциллограмма меандра показана на рисунке 9.
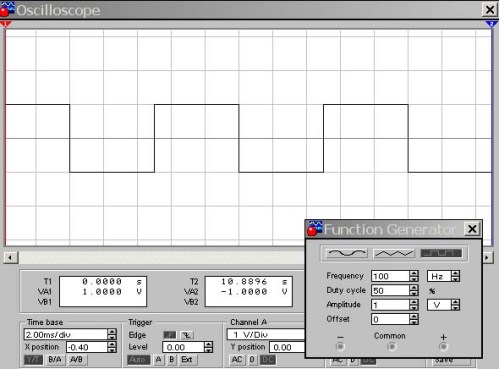
Рисунок 9. Осциллограмма меандра D=50%
Здесь вход осциллографа подключен к выходу функционального генератора, показанного тут же в нижнем углу рисунка. И вот тут внимательный читатель может задать вопрос: «Амплитуда выходного сигнала с генератора 1В, чувствительность входа осциллографа 1В/дел., а на экране прямоугольные импульсы с размахом 2В. Почему?»
Дело в том, что функциональный генератор выдает двухполярные прямоугольные импульсы относительно уровня 0В, примерно так же, как синусоида, с положительной и отрицательной амплитудой. Поэтому на экране осциллографа наблюдаются импульсы с размахом ±1В. На следующем рисунке изменим коэффициент заполнения Duty cycle, например, до 10%.
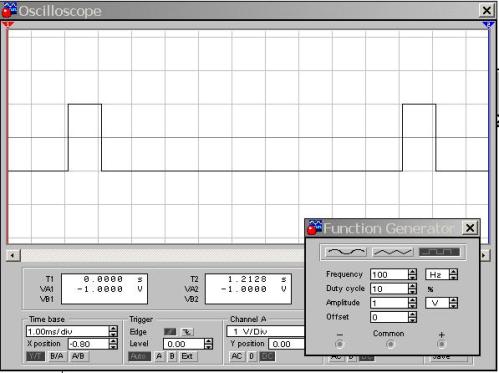
Рисунок 10. Прямоугольный импульс D=10%
Нетрудно видеть, что период следования импульсов составляет 10 клеток, в то время, как длительность импульса всего одна клетка. Поэтому D=1/10=0,1 или 10 %, что видно по настройкам генератора. Если воспользоваться формулой для подсчета скважности, то получится S = T / τ = 10 / 1 = 1 – величина безразмерная. Вот здесь можно сделать вывод, что Duty cycle намного наглядней характеризует импульс, чем скважность.
Собственно сам сигнал остался такой же, как на рисунке 9: прямоугольный импульс амплитудой 1В и частотой 100Гц. Изменяется только коэффициент заполнения или скважность, уж это как кому привычней и удобней. Но для удобства наблюдения на рисунке 10 длительность развертки снижена в два раза по сравнению с рисунком 9 и составляет 1мс/дел. Поэтому период сигнала занимает на экране 10 клеток, что позволяет достаточно легко убедиться, что Duty cycle составляет 10%. При пользовании реальным осциллографом длительность развертки выбирается примерно также.
Измерение напряжения прямоугольного импульса
Как было сказано в начале статьи, осциллограф измеряет напряжение, т.е. разность потенциалов между двумя точками. Обычно измерения проводятся относительно общего провода, земли (ноль вольт), хотя это необязательно. В принципе возможно измерение от минимального до максимального значения сигнала (пиковое значение, размах). В любом случае действия по измерению достаточно просты.
Прямоугольные импульсы чаще всего бывают однополярными, что характерно для цифровой техники. Как измерить напряжение прямоугольного импульса, показано на рисунке 11.
Рисунок 11. Измерение амплитуды прямоугольного импульса
Если чувствительность канала вертикального отклонения выбрана 1В/дел, то получается, что на рисунке показан импульс с напряжением 5,5В. При чувствительности 0,1В/дел. Напряжение будет всего 0,5В, хотя на экране оба импульса выглядят совершенно одинаково.
Что еще можно увидеть в прямоугольном импульсе
Прямоугольные импульсы, показанные на рисунках 9, 10 просто идеальные, поскольку синтезированы программой Electronics WorkBench. Да и частота импульсов всего 100Гц, поэтому проблем с «прямоугольностью» изображения возникнуть не может. В реальном устройстве при высокой частоте следования импульсы несколько искажаются, прежде всего, появляются различные выбросы и всплески, обусловленные индуктивностью монтажа, как показано на рисунке 12.
Рисунок 12. Реальный прямоугольный импульс
Если не обращать внимания на подобные «мелочи», то прямоугольный импульс выглядит так, как показано на рисунке 13.
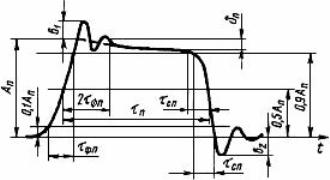
Рисунок 13. Параметры прямоугольного импульса
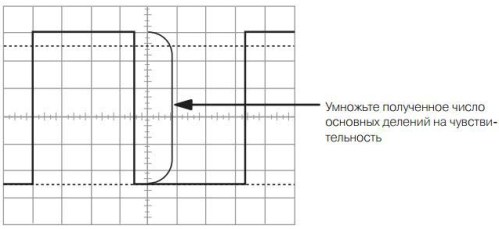
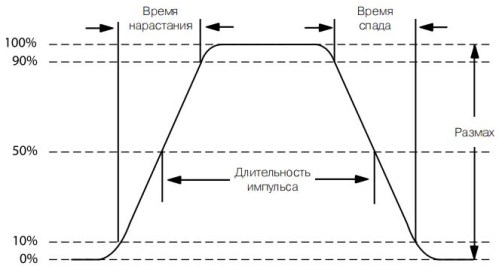
На рисунке показано, что передний и задний фронты импульса возникают не сразу, а имеют какое-то время нарастания и спада, несколько наклонены относительно вертикальной линии. Этот наклон обусловлен частотными свойствами микросхем и транзисторов: чем более высокочастотный транзистор, тем менее «завалены» фронты импульсов. Поэтому длительность импульса определяется по уровню 50% от полного размаха.
По этой же причине амплитуда импульса определяется по уровню 10…90%. Длительность импульса, так же, как и напряжение, определяется умножением числа делений горизонтальной шкалы на значение деления, как показано на рисунке 14.
На рисунке показан один период прямоугольного импульса, несколько отличного от меандра: длительность положительного импульса составляет 3,5 деления горизонтальной шкалы, а длительность паузы 3,8 деления. Период следования импульса составляет 7,3 деления. Такая картинка может принадлежать нескольким разным импульсам с различной частотой. Все будет зависеть от длительности развертки.
Предположим, что длительность развертки 1мс/дел. Тогда период следования импульса 7,3*1=7,3мс, что соответствует частоте F=1/T=1/7.3= 0,1428КГц или 143ГЦ. Если длительность развертки будет 1мкс/дел, то частота получится в тысячу раз выше, а именно 143КГЦ.
Пользуясь данными рисунка 14 нетрудно подсчитать скважность импульса: S=T/τ=7,3/3,5=2,0857, получается почти, как у меандра. Коэффициент заполнения Duty cycle D=τ/T=3,5/7,3=0,479 или 47.9%. При этом следует обратить внимание, что эти параметры ни в коем случае не зависят от частоты: скважность и коэффициент заполнения были подсчитаны просто по делениям на осциллограмме.
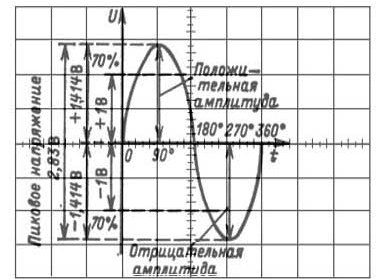
Рисунок 15. Параметры синусоиды
Очевидно, что для показанной на рисунке синусоиды чувствительность канала вертикального отклонения составляет 0,5В/дел. Остальные параметры нетрудно определить умножив число делений на 0,5В/дел.
Синусоида может быть и другой, которую придется измерять при чувствительности, например, 5В/дел. Тогда вместо 1В получится 10В. Однако, на экране изображение обеих синусоид выглядит абсолютно одинаково.
Временные параметры показанной синусоиды неизвестны. Если предположить, что длительность развертки 5мс/дел., период составит 20мс, что соответствует частоте 50ГЦ. Цифры в градусах на оси времени показывают фазу синусоиды, хотя для одиночной синусоиды это не особо важно. Чаще приходится определять сдвиг по фазе (непосредственно в миллисекундах или микросекундах) хотя бы между двумя сигналами. Лучше всего это делать с помощью двухлучевого осциллографа. Как это делается, будет показано чуть ниже.
Как осциллографом измерить ток
В некоторых случаях требуется измерение величины и формы тока. Например, переменный ток, протекающий через конденсатор, опережает напряжение на ¼ периода. Тогда в разрыв цепи включают резистор с небольшим сопротивлением (десятые доли Ома). На работу схемы такое сопротивление не влияет. Падение напряжения на этом резисторе покажет форму и величину тока, протекающего через конденсатор.
Примерно так же устроен обычный стрелочный амперметр, который включатся в разрыв электрической цепи. При этом измерительный резистор находится внутри самого амперметра.
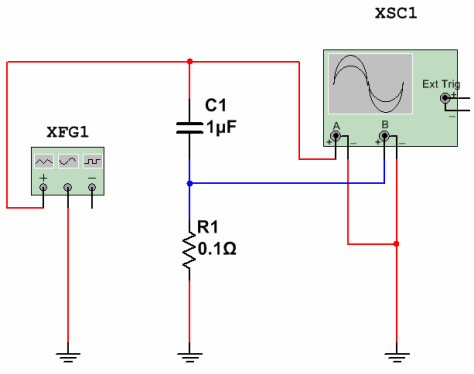
Схема для измерения тока через конденсатор показана на рисунке 16.
Рисунок 16. Измерение тока через конденсатор
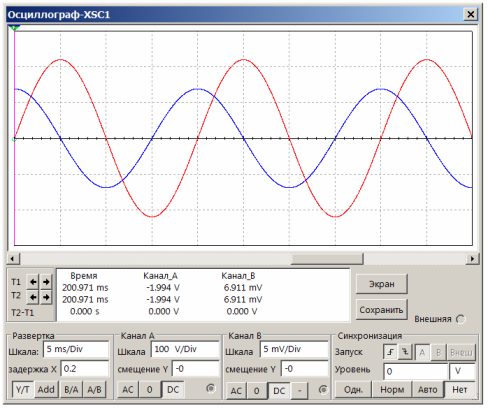
Синусоидальное напряжение частотой 50 Гц амплитудой 220 В с генератора XFG1 (красный луч на экране осциллографа) подается на последовательную цепь из конденсатора C1 и измерительного резистора R1. Падение напряжения на этом резисторе покажет форму, фазу и величину тока через конденсатор (синий луч). Как это будет выглядеть на экране осциллографа, показано на рисунке 17.
Рисунок 17. Ток через конденсатор опережает напряжение на ¼ периода
При частоте синусоиды 50 Гц и развертке 5 ms/Div один период синусоиды занимает 4 деления по оси X, что очень удобно для наблюдения. Нетрудно видеть, что синий луч опережает красный ровно на 1 деление по оси X, что соответствует ¼ периода. Другими словами ток через конденсатор опережает по фазе напряжение, что полностью соответствует теории.
Чтобы рассчитать ток через конденсатор достаточно воспользоваться законом Ома: I = U/R. При сопротивлении измерительного резистора 0,1Ом падение напряжения на нем 7мВ. Это амплитудное значение. Тогда максимальный ток через конденсатор составит 7/0,1=70мА.
Измерение формы тока через конденсатор не является какой-то очень актуальной задачей, тут все ясно и без измерений. Вместо конденсатора может быть любая нагрузка: катушка индуктивности, обмотка электродвигателя, транзисторный усилительный каскад и многое другое. Важно, что именно таким методом можно исследовать ток, который в некоторых случаях значительно отличается по форме от напряжения.