Как измерить длину окружности измерением
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
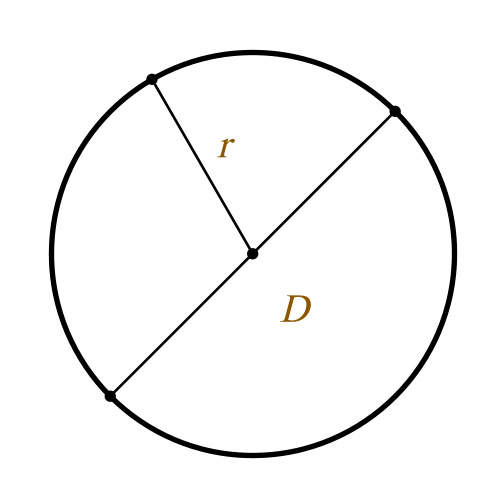
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, равное 3,14
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку « O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Диаметр окружности обозначается буквой « D ». На рисунке выше — это отрезок « BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение « D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2 π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Определите диаметр окружности, если её длина равна 56,52 дм. ( π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки « A » и « B ». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга « AB » и черная дуга « AB ». Точки « A » и « B » называют концами дуг.
Соединим точки « A » и « B » отрезком. Полученный отрезок называют хордой.
Точки « A » и « B » делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга « AB ».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Изучение способов нахождения длины окружности



Рубрика: Математика: алгебра и начала анализа, геометрия
Дата публикации: 29.12.2019 2019-12-29
Статья просмотрена: 2485 раз
Библиографическое описание:
Бородин, М. В. Изучение способов нахождения длины окружности / М. В. Бородин, О. Б. Никитина. — Текст : непосредственный // Юный ученый. — 2020. — № 1 (31). — С. 37-42. — URL: https://moluch.ru/young/archive/31/1837/ (дата обращения: 23.12.2021).
В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.
Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.
В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.
В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.
Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.
В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.
Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.
Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.
Основные понятия
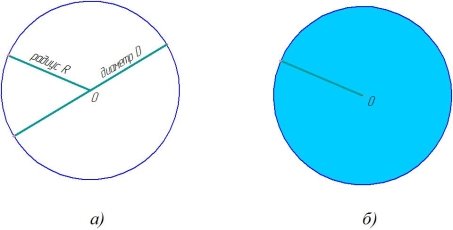
Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).
Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).
Можно сказать, что окружность является границей круга.
Основные линии окружности — радиус и диаметр (рисунок 1,а).
Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.
Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.
Рис. 1. Окружность и круг
Способы нахождения длины окружности
Рассмотрим некоторые возможные способы нахождения длины окружности.
Нахождение длины окружности с помощью нити
Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.
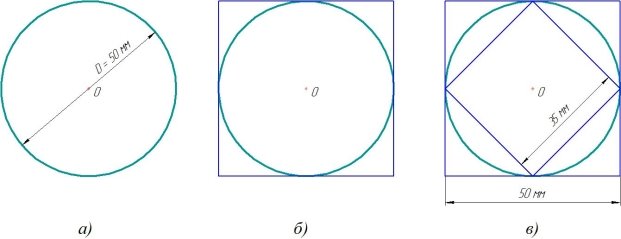
Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).
Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.
То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.
Рис. 2. Нахождение длины окружности с помощью нити
Нахождение длины окружности с помощью квадратов
Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).
Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).
Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.
Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.
Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.
Найдем периметры квадратов:
Периметр внутреннего квадрата Р внутр = 35+35+35+35 = 435= 140 (мм);
Периметр внешнего квадрата Р внешн = 50+50+50+50= 450 = 200 (мм).
Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).
Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.
Нахождение длины окружности с помощью многоугольников
Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.
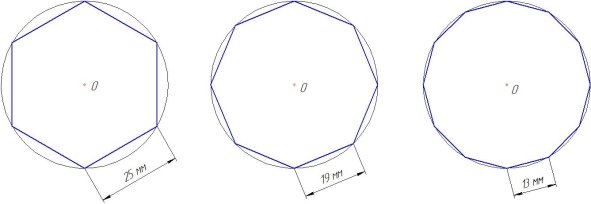
Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).
Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.
Периметр шестиугольника (обозначим его Р 6 ) равен:
Р 6 = 25+25+25+25+25+25= 625 = 150 (мм).
Найдем периметры восьмиугольника Р 8 и двенадцатиугольника Р 12 :
Р 8 = 19+19+19+19+19+19+19+19 = 819 = 152 (мм);
Р 12 = 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).
Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.
Получение формулы длины окружности экспериментальным методом
От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.
Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.
Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).
Рис. 5. Подготовка к эксперименту
Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).
Рис. 6. Проведение эксперимента
В ходе эксперимента мы получили следующие результаты (рисунок 7).
Длина окружности, диаметр которой D 1 = 50мм, равна 157мм, то есть L 1 =157 мм.
Длина окружности диаметром D 2 =100 мм равна L 2 =314 мм.
Длина окружности диаметром D 3 =200 мм равна L 3 =628 мм.
Рис. 7. Результаты эксперимента
Представим полученные результаты в виде таблицы.
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
r – радиус окружности
D – диаметр окружности
L – длина окружности
Пример нахождения длинны окружности
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр