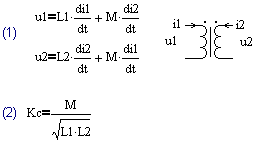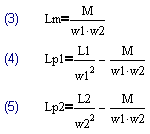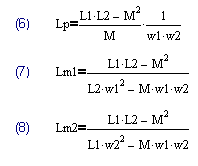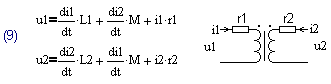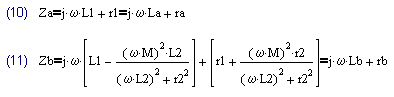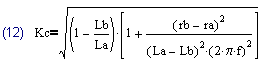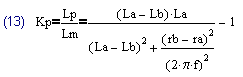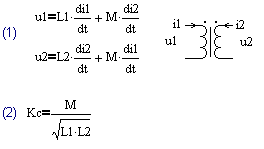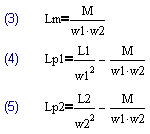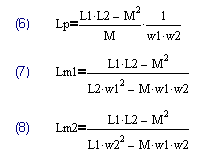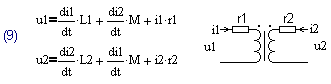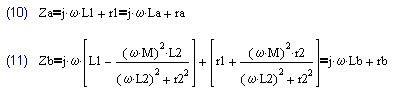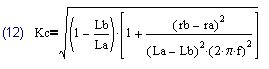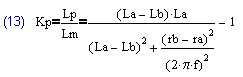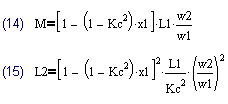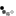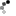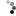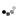Как измерить индуктивность намагничивания трансформатора
ТЕМА: Измеряем индуктивность выходных трансформаторов
Измеряем индуктивность выходных трансформаторов 13 март 2018 22:03 #3194
Измерение индуктивности. Лабораторная работа №1, она же и последняя
Итак, займемся измерением индуктивности выходных трансформаторов и дросселей.
На форуме у Василича для этого есть схема.
Измеряем индуктивность выходных трансформаторов 13 март 2018 22:17 #3195
Измеряем индуктивность выходных трансформаторов 13 март 2018 22:24 #3196
Переходим к измерениям. Подопытным клиентом выступил выходной трансформатор габаритной мощностью 80Вт.
Сначала контролируем напряжение питания схемы, у меня использован трансформатор мощностью 15Вт на 12В. В зависимости от времени суток напряжение слегка гуляет, поэтому оперативный режим его контроля крайне полезен. Далее выставляем переменными резисторами половину этого напряжения. После переключаем прибор в режим измерения сопротивления и измеряем его. По формуле вычисляем индуктивность первичной обмотки. Ого, отличный результат.
Измеряем напряжение питания схемы.
С помощью переменных резисторов устанавливаем половину напряжения питания
Переключаем прибор в режим измерения сопротивления.
Измеряем тестером сопротивление переменных резисторов
Измеряем индуктивность выходных трансформаторов 13 март 2018 22:34 #3197
На оном из форумов наблюдал, как некоторые умные черепа, мягко сказать, критикуют этот метод измерения. Типа, все это ерунда, погрешность этого метода зашкаливает и т.д. и т.п.
Для такого типа неверующих я провел следующие измерения.
С помощью резисторов выставляем половину напряжения питания.
Обмотки дросселя (основная и дополнительная) соединены последовательно.
Как измерить индуктивность намагничивания трансформатора
Непосредственно пользоваться системой (1) при анализе преобразователей не вполне удобно, так как в неё в явном виде не входит коэффициент трансформации (отношение числа витков обмоток). Поэтому зачастую применяются производные от (1) схемы замещения трансформатора, параметры которых могут быть рассчитаны, либо измерены экспериментально и отражают его физические параметры, такие как числа витков обмоток, индуктивности намагничивания и рассеяния. Среди наиболее простых моделей, учитывающих рассеяние и содержащие в явном виде коэффициент трансформации можно отметить Т- и П- образные модели [1].
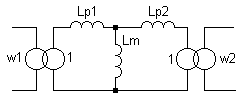
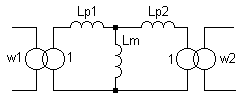
На рис.1 показана модель трансформатора, являющаяся одним из вариантов Т-образной модели. Данная модель содержит два идеальных трансформатора с коэффициентами трансформации w1:1 и w2:1 и приведенные к единичному витку: индуктивность намагничивания Lm и две индуктивности рассеяния Lp1 и Lp2, связанные с соответствующими обмотками. Параметры этой модели связаны с параметрами системы (1) через (3)-(5).
Рис.1 Т-образная модель трансформатора
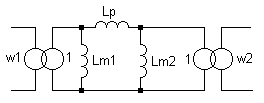
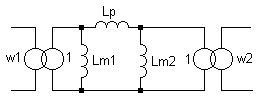
Аналогичная П-образная модель трансформатора показана на рис.2. Её параметры связаны с параметрами системы (1) через (6)-(8)
Рис.2 П-образная модель трансформатора
Измерение импеданса
Методы измерения параметров различных частото-зависимых моделей трансформаторов как правило строятся на экспериментальном снятии частотных характеристик импеданса по первичной стороне трансформатора [2]. Измерения проводят при двух условиях: разомкнутой и замкнутой вторичной обмотки. Для измерений применяется частотный анализатор, а результатом является довольно сложная модель, полно отражающая частотную характеристику трансформатора как некоторого четырехполюсника «черного ящика» (black box), «внутренности» которого вообще-говоря могут никак не быть связаны с его физическими параметрами. Сложность таких моделей, трудоемкость измерений либо необходимость использовать специализированное оборудованиене не всегда оправданы. Зачастую при анализе импульсных преобразователей (особенно это касается аналитических расчетов) пользуются самыми простыми моделями, подобными описанным выше. Избыточным оказывается учет в модели таких факторов, как наличие резонанса, потерь в трансформаторе и других.
Особенностью использования LRC-метра в качестве измерительного прибора является измерение импеданса на фиксированой частоте (1 кГц), которая как правило существенно ниже чем частота на которой используется трансформатор (20. 500 кГц). Поэтому небходимо обязательно учитывать резистивную составляющую, которая на низкой частоте для этих трансформаторов существенна и играет важную роль при использовании методики измерения параметров, предполагающей измерение импеданса по первичной обмотке при условиях разомкнутой либо замкнутой вторичной обмотки.
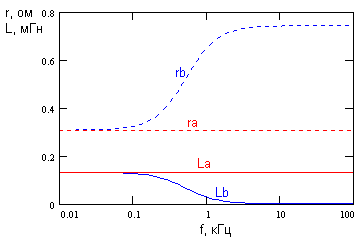
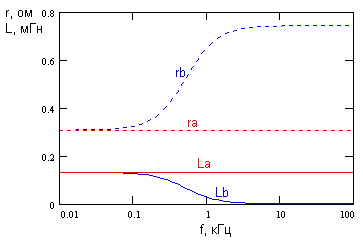
Как видно из рисунка, в области частот выше 100 кГц (то есть в области рабочих частот трансформатора), характеристики моделей, построенных без учета и с учетом сопротивлений обмоток, практически совпадают. Поэтому при анализе допустимо использовать модель без сопротивлений (что упрощает расчеты). Однако поскольку измерения импеданса с помощью LRC-метра проводятся на низкой частоте, сопротивления обмоток необходимо учитывать в расчете параметров трансформатора. Частота измерения должна быть всеже достаточно высока, для того чтобы импедансы при разных условиях по вторичной обмотке заметно отличались. Для случая, показанного на рис.3 частота измерения 1кГц вполне приемлима, тогда как частота 120 Гц очевидно слишком низкая для измерений.
Трасформатор с учетом сопротивлений
При учете сопротивлений обмоток, получаем следующую систему уравнений, описывающих трансформатор:
Располагая соотношениями (10), (11) можно выразить коэффициент связи трансформатора (2) через значения измеренных параметров:
Иногда вместо коэффициента связи оказывается удобно пользоваться непосредственно отношением индуктивности рассеяния к индуктивности намагничивания Kp. Например исходя из этого отношения определялись потери в снаббере обратноходового преобразователя в [3]. В этом случае это отношение можно представить как (13). В этой формуле для Т-образной модели трансформатора (рис.1) индуктивность рассеяния Lp следует понимать как сумму индуктивностей рассеяния обмоток Lp1+Lp2, а для П-образной модели (рис.2) индуктивность намагничивания Lm следует понимать как параллельное соединение индуктивностей Lm1 и Lm2, то есть
Рис.4 Частотная зависимость измеряемых величин
Определение параметров Т- и П- образных моделей трансформаторов
Как только стали известны значения L1, L2, M, мы можем легко рассчитать параметры Т-образной модели трансформатора по (3)-(5) и П-образной модели по (6)-(8).
Экспериментальная проверка
Экспериментальная проверка данного подхода заключалась в следующем:
Выводы
Предложена методика определения коэффициента связи трансформатора, параметров линейного дифференциального уранения, описывающего трансформатор, а также параметров двух простых схемотехнических моделей трансформатора по результатам измерений импеданса по первичной стороне с помощью стандартного LRC-метра при условиях разомкнутой и замкнутой вторичной обмотки. Показаны ограничения данного метода, связанные с выбором частоты измерения.
Данный способ, не использующий данных измерения по вторичной стороне, хорошо подходит для измерения параметров трансформаторов, имеющих малое число витков во вторичной обмотке.
Литература
Как измерить индуктивность намагничивания трансформатора
Трансформатор с учетом рассеяния
Непосредственно пользоваться системой (1) при анализе преобразователей не вполне удобно, так как в неё в явном виде не входит коэффициент трансформации (отношение числа витков обмоток). Поэтому зачастую применяются производные от (1) схемы замещения трансформатора, параметры которых могут быть рассчитаны, либо измерены экспериментально и отражают его физические параметры, такие как числа витков обмоток, индуктивности намагничивания и рассеяния. Среди наиболее простых моделей, учитывающих рассеяние и содержащие в явном виде коэффициент трансформации можно отметить Т- и П- образные модели [1].
На рис.1 показана модель трансформатора, являющаяся одним из вариантов Т-образной модели. Данная модель содержит два идеальных трансформатора с коэффициентами трансформации w1:1 и w2:1 и приведенные к единичному витку: индуктивность намагничивания Lm и две индуктивности рассеяния Lp1 и Lp2, связанные с соответствующими обмотками. Параметры этой модели связаны с параметрами системы (1) через (3)-(5).
Рис.1 Т-образная модель трансформатора
Аналогичная П-образная модель трансформатора показана на рис.2. Её параметры связаны с параметрами системы (1) через (6)-(8)
Рис.2 П-образная модель трансформатора
Измерение импеданса
Методы измерения параметров различных частото-зависимых моделей трансформаторов как правило строятся на экспериментальном снятии частотных характеристик импеданса по первичной стороне трансформатора [2]. Измерения проводят при двух условиях: разомкнутой и замкнутой вторичной обмотки. Для измерений применяется частотный анализатор, а результатом является довольно сложная модель, полно отражающая частотную характеристику трансформатора как некоторого четырехполюсника «черного ящика» (black box), «внутренности» которого вообще-говоря могут никак не быть связаны с его физическими параметрами. Сложность таких моделей, трудоемкость измерений либо необходимость использовать специализированное оборудованиене не всегда оправданы. Зачастую при анализе импульсных преобразователей (особенно это касается аналитических расчетов) пользуются самыми простыми моделями, подобными описанным выше. Избыточным оказывается учет в модели таких факторов, как наличие резонанса, потерь в трансформаторе и других.
Особенностью использования LRC-метра в качестве измерительного прибора является измерение импеданса на фиксированой частоте (1 кГц), которая как правило существенно ниже чем частота на которой используется трансформатор (20. 500 кГц). Поэтому небходимо обязательно учитывать резистивную составляющую, которая на низкой частоте для этих трансформаторов существенна и играет важную роль при использовании методики измерения параметров, предполагающей измерение импеданса по первичной обмотке при условиях разомкнутой либо замкнутой вторичной обмотки.
Как видно из рисунка, в области частот выше 100 кГц (то есть в области рабочих частот трансформатора), характеристики моделей, построенных без учета и с учетом сопротивлений обмоток, практически совпадают. Поэтому при анализе допустимо использовать модель без сопротивлений (что упрощает расчеты). Однако поскольку измерения импеданса с помощью LRC-метра проводятся на низкой частоте, сопротивления обмоток необходимо учитывать в расчете параметров трансформатора. Частота измерения должна быть всеже достаточно высока, для того чтобы импедансы при разных условиях по вторичной обмотке заметно отличались. Для случая, показанного на рис.3 частота измерения 1кГц вполне приемлима, тогда как частота 120 Гц очевидно слишком низкая для измерений.
Трасформатор с учетом сопротивлений
При учете сопротивлений обмоток, получаем следующую систему уравнений, описывающих трансформатор:
Располагая соотношениями (10), (11) можно выразить коэффициент связи трансформатора (2) через значения измеренных параметров:
Иногда вместо коэффициента связи оказывается удобно пользоваться непосредственно отношением индуктивности рассеяния к индуктивности намагничивания Kp. Например исходя из этого отношения определялись потери в снаббере обратноходового преобразователя в [3]. В этом случае это отношение можно представить как (13). В этой формуле для Т-образной модели трансформатора (рис.1) индуктивность рассеяния Lp следует понимать как сумму индуктивностей рассеяния обмоток Lp1+Lp2, а для П-образной модели (рис.2) индуктивность намагничивания Lm следует понимать как параллельное соединение индуктивностей Lm1 и Lm2, то есть
Рис.4 Частотная зависимость измеряемых величин
Определение параметров Т- и П- образных моделей трансформаторов
Как только стали известны значения L1, L2, M, мы можем легко рассчитать параметры Т-образной модели трансформатора по (3)-(5) и П-образной модели по (6)-(8).
Экспериментальная проверка
Экспериментальная проверка данного подхода заключалась в следующем:
Выводы
Предложена методика определения коэффициента связи трансформатора, параметров линейного дифференциального уранения, описывающего трансформатор, а также параметров двух простых схемотехнических моделей трансформатора по результатам измерений импеданса по первичной стороне с помощью стандартного LRC-метра при условиях разомкнутой и замкнутой вторичной обмотки. Показаны ограничения данного метода, связанные с выбором частоты измерения.
Данный способ, не использующий данных измерения по вторичной стороне, хорошо подходит для измерения параметров трансформаторов, имеющих малое число витков во вторичной обмотке.
Как рассчитать индуктивность силового трансформатора, формулы и примеры
Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
Конструкция и принцип действия силового трансформатора
В основе конструкции любого трансформатора находятся следующие элементы:
В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.
ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.
Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.
Физическое понятие индуктивности обмоток
Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.
Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.
При постоянном токе говорить об индуктивности бессмысленно.
В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.
Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
µ0 – магнитная постоянная;
µ – магнитная проницаемость сердечника;
N – количество витков;
S – площадь одного витка;
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Пример расчета
К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:
Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.
Тема: Помогите с расчетом индуктивности рассеяния
Опции темы
Помогите с расчетом индуктивности рассеяния на центральном керне трансформатора ETD29/16/10 для LLC источника питания
Итак для эксперимента намотал первичку проводом 0,25 (диаметр с учетом изоляции) 50 витков виток к витку— длина намотки-b1- составила 13,6мм;толщина-d- понятно равна толщине провода;
Далее 7 витков вторички тем же проводом—длина-b2- обмотки 1,9мм;
диаметр каркаса 11,65мм длина каркаса 19,52мм ;средняя длина витка получилась 37,4 мм
По известной формуле; [IMG]file:///C:\Users\jiol\AppData\Local\Temp\msohtml1\01\clip_image002.gif[/IMG]
интересно, почему при их педантичности то.
В данных даташитах подгонка индуктивности намагничивания производиться введением зазора, при этом индуктивность рассеивания не меняется(уменьшается на единицы процентов)
Индуктивность рассеивания это обратная величина Ксвязи между обмотками с учетом св-в сердечника.
Вычисляется отношением L закороченной обмотки вторички к L открытой *100%
получается где то в районе 360 микрогенри а на трансе при реале который намотал сейчас 56 первичка и 8 и 8 вторичка
Я импульсниками не занимаюсь и PI Expert Design Software не пользуюсь.
Скорее всего, в этом вопросе, Alex Torres сможет помочь.
получается где то в районе 360 микрогенри а на трансе при реале который намотал сейчас 56 первичка и 8 и 8 вторичка
Ради интереса измерил индуктивность обмотки трансика на феррите на разных уровнях тест-сигнала для частоты 1кГц.
Так вот, при уровне в 50мВ и 1В, разница получилась в 20% При бОльшем напряжении она будет еще больше.
Чем меньше напряжение тест-сигнала, тем меньше значение индуктивности. Кстати, разброс мю у феррита более 20%, обычное дело.
ДА не в 20% дело дело в том что формула прописанная во многих источниках дает 7-10 кратную погрешность
Вот по ссылке формула 20 http://www.st.com/web/en/resource/te. CD00004440.pdf
дает достаточно точный результат но там вместо толщины обмотки (как в классической формуле) стоит расстояние от центра катушки до верхнего слоя обмотки
если считать по ней для моих трансов получается достаточно точно
но при этом если это расстояние равно 6 мм как в моем случае индуктивность получается 270 мкг
но если обмотка однослойная то расстояние равно 5,7 мм и расчет дает 290 мкг а измерения показывают 600мкг
,что то с однослойной обмоткой везде какая то мистика
Инд рассеивания зависит от связи между обмотками. По моему мнению ее не надо считать, тут только эксперимент поможет. Связь между обмотками зависит от их исполнения и взаимного расположения т.е. физическое расположение, геометрия, ни одна формула не сможет дать адекватный результат. От проницаемости сердечника инд рассеивания теоретически не зависит, однако на практике зависимость чуток имеется, но она мизерная, поэтому про это можно забыть сразу. В интернет есть об этом заметки.
Измерять инд рассеивания тестером за 40 баксов я бы тоже не стал. Помню даже аппарат за безумные деньги меня подвел. Делайте LC параллельный колебательный контур и по его резонансной частоте рассчитывайте реальную инд. для этого нужен осциллограф и конденсатор резистор и блок питания или батарейка.