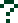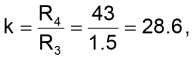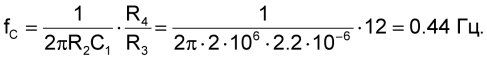Как измеряют постоянную составляющую сигнала

Автоматика.
Автоматизация.
Электротехнические
комплексы и системы.

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ СОСТАВЛЯЮЩЕЙ СИГНАЛОВ МЕТОДОМ АДАПТАЦИИ

Шутеев Э.И., Белокопытов Д.О.

Введение

При измерении характеристик динамических объектов, полученные результаты оказываются зашумленными или искаженными, что в большинстве случаев не позволяет получить результат с требуемой точностью. Связано это с тем, что объекты окружающего мира являются динамическими системами и обладают своими внутренними изменениями, деформациями, колебаниями, а вследствие чего и шумами. В статье рассматривается возможность повышение точности определения параметров сигналов динамических систем при помощи адаптивной фильтрации. Основа метода заключается в том, что система моделирует собственную весовую функцию для каждого нового сигнала.

Адаптивные устройства обработки данных отличаются наличием определенной связи параметров передаточной функции с параметрами входных, выходных, ожидаемых, прогнозируемых и прочих дополнительных сигналов или с параметрами их статистических соотношений, что позволяет самонастраиваться на оптимальную обработку сигналов. В простейшем случае, адаптивное устройство содержит программируемый фильтр обработки данных и блок (алгоритм) адаптации, который на основании определенной программы анализа входных, выходных и прочих дополнительных данных вырабатывает сигнал управления параметрами программируемого фильтра.

Последовательность получения какого-либо параметра динамической системы изображена на рис. 1 [1]. На исследуемый объект, кроме определяемого воздействия, могут действовать и различные внешние факторы среды, которые вносят аддитивную составляющую помехи. Также сам объект, являясь сложной системой, вносит мультипликативную составляющую помехи. Далее уже искаженный физический параметр, определенным способом преобразуется в электрический, затем следует аналогово-цифровое преобразование, приведение полученного значения по заданной функции к нормальному виду.

Рис. 1 Структурная схема получения параметра динамической системы

Постановка задачи

Полученные в результате аналогово-цифрового преобразования и нормализации данные в большинстве случаев не будут пригодны для дальнейшего использования без предварительной обработки, в процессе которой минимизируются всевозможные помехи и шумы. Одним из способов устранения возникших искажений является фильтрация [1,2], при этом необходимо точно знать либо то что требуется получить, либо то что требуется удалить из сигнала. Однако, когда речь идёт о динамических системах заранее предположить что либо точно нельзя, определены только общие черты сигнала и помехи. Поэтому, даже применяя фильтрацию к одному классу динамических систем, в большинстве случаев для получения результата с ожидаемой точностью, не достаточно лишь определить тип фильтрации. Возникает необходимость подстройки фильтра в процессе фильтрации, то есть его адаптации к входному воздействию.

Рис. 2 Диаграмма взвешивания состава

На рис. 3 и рис. 4 изображены увеличенные части рис. 2, это и есть зашумленный сигнал при взвешивании осей тепловоза и вагона.

Рис. 3 Зашумленный сигнал (ось тепловоза)

Рис. 4 Зашумленный сигнал (ось вагона)

Целью данной работы является поиск алгоритма и структуры системы использующей адаптивную фильтрацию для более точного определения параметров динамических объектов. В результате адаптации есть возможность получения оптимального КИХ-фильтра или окна для последующего синтеза КИХ-фильтров [3]. Целесообразность такого подхода и будет рассмотрена далее.

Описание предложенного адаптивного метода

На рис. 6 изображен зашумленный сигнал, из которого необходимо выделить полезную составляющую.

Рис. 6 Зашумленный сигнал

Исходя из метода окон [2], можно использовать ту же формулу для определения постоянной составляющей сигнала, но только в качестве весовых коэффициентов взять коэффициенты КИХ-фильтра, полученного на основе адаптивного фильтра.

Формула определения постоянной составляющей:

Следующая формула получается подстановкой в формулу (2) вместо x ( t ) формулы (1), и умножением обеих частей уравнения на знаменатель:

Раскрыв в правой части уравнения скобки и учитывая то, что интеграл суммы равен сумме интегралов, а произведение подынтегральной функции на константу равносильно произведению самого интеграла на эту константу, получается:

Следовательно, для выполнения исходной формулы должно выполняться условие:

Формула (5) является условием подавления помехи КИХ-фильтра [1], то есть необходимо выбрать такой КИХ-фильтр, после прохождения через который аддитивная помеха станет близкой к нулю. Такой фильтр можно получить с помощью адаптивной фильтрации, при этом адаптивный фильтр можно адаптировать к любой константе К, соизмеримой по величине с определяемой.

В результате моделирования были исследованы две различные адаптивные схемы позволяющие подавить помеху рис.7 и рис.8. При адаптивном моделировании обязательно требуется образцовый сигнал, а как правило в реальных условиях его нет, поэтому были испробованы различные способы его замены. Так на рис.7. приведена структура одной из наиболее результативных моделей решения проблемы. В приведенной модели адаптивный фильтр включен последовательно с системой, что позволяет в результате адаптации получить обратную модель системы. Образцовый сигнал, необходимый для адаптации фильтра, является константой. Далее полученные в результате адаптации коэффициенты адаптивного фильтра, подставляются в передаточную функцию, в результате чего получается настроенный на определенную помеху неадаптивный фильтр, то есть режекторный КИХ-фильтр. Теперь, пропуская зашумленный сигнал уже через полученный КИХ-фильтр, на выходе получаем достаточно точное подобие исходного чистого сигнала, среднее значение которого и будет соответствовать искомому параметру.

В изображенной на рис. 7 модели, в качестве входного воздействия используются прямоугольные импульсы. С помощью сумматора на них накладываются две гармонические составляющие, с частотами соизмеримыми с реальными помехами. Затем эта смесь пропускается через рекурсивное звено, представленное передаточной функцией. В результате, окончательно искаженный сигнал поступает на вход адаптивного фильтра и параллельно на вход КИХ-фильтра, представленного передаточной функцией. В качестве адаптивного фильтра был выбран фильтра Калмана как наиболее подходящий, так как он предназначен для минимизации дисперсии оценки векторного случайного процесса x(k), изменяющегося во времени следующим образом:

x (k+1)= Φ (k) x (k)+v(k),

где Φ(k) — матрица перехода, v(k) — случайный вектор (шум процесса) [4]. Что близко к поставленной задаче. На вход ошибки адаптации фильтра, подается разница между константой и сигналом с выхода фильтра. Полученные же в результате адаптации коэффициенты фильтра, записываются в специальное окно отображения результата и сохраняются в числовом векторе, используемом в дальнейшем для подстановки в передаточную функцию. В окне симулятора Scope отображены интересующие нас сигналы: входной, зашумленный, сигнал ошибки адаптации и отфильтрованный сигнал.

Рис. 7 Модель исследуемой системы

Суть данной модели в том, что конечный результат получается при делении, где делимым является сумма произведений коэффициентов фильтра на соответствующие отсчеты сигнала, а делителем сумма всех коэффициентов фильтра, это отражает следующая формула:

где w_ai – коэффициенты адаптивного фильтра,

X ₀ – амплитуда зашумленного сигнала.

Вернувшись к первой модели и проанализировав получаемые в результате адаптации коэффициенты фильтра, можно сделать вывод, что каждый коэффициент адаптивного фильтра складывается из двух частей, одна из которых служит для нормализации амплитуды входного сигнала к амплитуде образцового, а вторая для удаления искажающей составляющей сигнала. Исходя из этого, можно сделать вывод что первое слагаемое b_i изменяется при изменении амплитуды образцового сигнала и пропорциональна этому изменению, а второе является константой c_i и зависит лишь от типа помехи.

Рис. 8 Модель системы с паралельно включенным адаптивным фильтром

Следовательно, справедливо следующее равенство:

Проверив полученное выражение экспериментально и сведя результаты эксперимента в таблицу 1, проанализируем погрешность измерения.

Источник

Способ измерения постоянной составляющей гармонического сигнала

Изобретение относится к области электрорадиоизмерений и может быть использовано для измерения постоянной составляющей гармонического сигнала за малое время измерения, в том числе и за время, меньшее периода (полупериода) гармонического сигнала и некратное периоду сигнала, с повышенной точностью и помехоустойчивостью.

Известен способ измерения постоянной составляющей периодического сигнала, по которому независимо выделяют и усредняют значения полуволн положительной полярности сигнала, независимо выделяют и усредняют значения полуволн отрицательной полярности сигнала, непрерывно находят разности полученных величин для определения постоянной составляющей (см. а.с. СССР 951157, G 01 R 19/02).

Недостатком данного способа является низкое быстродействие, обусловленное тем, что нахождение постоянной составляющей может производиться не чаще, чем через период измеряемого сигнала.

Известен способ измерения постоянной составляющей периодического сигнала, основанный на фиксировании каждого экстремума измеряемого сигнала и снятии мгновенного значения сигнала через интервал времени отсчета, равный четверти периода переменной составляющей сигнала. По зафиксированному значению выборки до следующей выборки судят о значении постоянной составляющей (см. а.с. СССР 1126886, G 01 R 19/02).

Недостатком данного способа является низкое быстродействие, так как значение постоянной составляющей определяется не чаще, чем через полпериода измеряемого сигнала, а также низкая помехоустойчивость, так как точность определения постоянной составляющей зависит от точности определения экстремума и точности взятия мгновенной выборки, поэтому при воздействии на измеритель шума совместно с измеряемым сигналом постоянная составляющая будет измеряться с большой погрешностью, а при значительном уровне шума измерения станут вообще невозможными.

Наиболее близким по технической сущности к предлагаемому способу является способ, основанный на интегрировании измеряемого сигнала за время, равное периоду измеряемого гармонического сигнала, и вычислении постоянной составляющей по результату интегрирования (см. кн. Ф.В. Кушнир. Электрорадиоизмерения/Учебное пособие для вузов. Л.: Энергоатомиздат, 1983, с.52).

Данный способ обеспечивает оптимальное по критерию максимального правдоподобия измерение постоянной составляющей гармонического сигнала при времени измерения, равном или кратном периоду этого гармонического сигнала. При этом обеспечивается минимально возможная погрешность при воздействии на вход измерителя флуктуационного шума. Однако при времени измерения, меньшем или некратном периоду сигнала, возникает большая систематическая погрешность, и измерение постоянной составляющей в этих условиях становится практически невозможным. Продемонстрируем сказанное следующим образом.

В основу настоящего изобретения положена задача осуществления измерения постоянной составляющей гармонического сигнала при времени измерения менее и некратном периоду гармонического сигнала без систематической погрешности при априорно неизвестных фазовом сдвиге и амплитуде измеряемого гармонического сигнала.

Сущность предлагаемого способа можно пояснить следующим образом.

Предлагаемый способ обеспечивает измерение постоянной составляющей гармонического сигнала вида (3) с систематической погрешностью, равной нулю при произвольном времени измерения при априорно неизвестных как амплитуде, так и фазовом сдвиге измеряемого сигнала. Для применения предлагаемого способа необходимо априорное знание только частоты измеряемого сигнала для формирования косинусной составляющей опорного сигнала. Чтобы убедиться в этом, найдем математическое ожидание результата измерения по предлагаемому способу. Для этого подставим в (6) измеряемый сигнал без шума (n(t)=0). Тогда для составляющих (2), (7-9) после взятия интегралов получим:
= E₀+ES_m0sin₀ (10),


* = E (13),
где , а Е определяется из (5).

Подставив (10-13) в (6), получим Е_изм = Е₀, причем данное равенство справедливо для любого Т_u, как кратного, так и некратного периоду гармонического сигнала, в том числе и для Т_u меньше периода (полупериода) сигнала, и не зависит от амплитуды и фазового сдвига (S_m0, ₀) измеряемого сигнала.

При анализе случайной погрешности предлагаемого способа измерения постоянной составляющей можно показать с использованием функции правдоподобия для сигнала вида (3), что данный способ имеет минимально возможную погрешность, так как способ получен путем исследования функции правдоподобия и является поэтому оптимальным по критерию максимального правдоподобия для способов измерения параметров гармонического сигнала за время, менее или некратное периоду сигнала.

На фиг. 1 приведена структурная схема одного из вариантов устройства, реализующего предлагаемый способ.

Устройство содержит тактовый генератор 1, блок памяти 2, цифроаналоговый преобразователь 3, перемножитель 4, квадратор 5, интеграторы 6, 7, 8 и 9, вычислительный блок 10, индикатор 11, формирователь импульсов пуска 12, времязадающий элемент 13 и формирователь импульсов остановки 14, причем тактовый генератор 1 выходом соединен с входом блока памяти 2, который выходом соединен с входом цифроаналогового преобразователя 3, формирующего косинусную составляющую опорного сигнала, выход которого соединен с первым выходом перемножителя 4, с входом квадратора 5 и входом интегратора 9, второй вход перемножителя 4 соединен с входом интегратора 6 и служит для подачи измеряемого сигнала, выходы перемножителя 4 и квадратора 5 соединены с входами интеграторов 7 и 8 соответственно, а выходы всех интеграторов 6, 7, 8 и 9 соединены с соответствующими входами вычислительного блока 10, который выходом подключен к входу индикатора 11. Выход формирователя импульсов пуска 12 соединен с входом время задающего элемента 13, а выход времязадающего элемента 13 соединен с первыми управляющими входами интеграторов 6, 7, 8 и 9 и является управляющим входом тактового генератора 1 и входом формирователя импульсов остановки 14, выход которого соединен с вторыми управляющими входами интеграторов 6, 7, 8 и 9 и с управляющим входом индикатора 11.

Способ реализуется следующим образом.

Момент начала измерения формируется формирователем импульсов пуска 12, работающего в ручном или автоматическом режимах. Времязадающим элементом 13 формируется импульс, равный по длительности времени измерения Т_u, который подают на управляющий вход тактового генератора 1, на первые управляющие входы интеграторов 6, 7, 8 и 9 и на вход формирователя импульсов остановки 14. В течение времени T_u тактовым генератором 1 осуществляется выборка значений опорного сигнала, записанных в блоке памяти 2, которые в цифровом виде поступают на вход цифроаналогового преобразователя 3, на выходе которого и формируется аналоговый сигнал, являющийся косинусной составляющей опорного сигнала с экстремумом в середине измерительного интервала, поступающий затем на перемножитель 4, квадратор 5 и интегратор 9. Сигналы, являющиеся результатом перемножения измеряемого сигнала и косинусной составляющей опорного сигнала, возведения в квадрат косинусной составляющей опорного сигнала, а также косинусная составляющая опорного сигнала и сам измеряемый сигнал интегрируются в течение времени Т_u. После окончания интегрирования результаты запоминаются на время, равное длительности импульса с выхода формирователя импульсов остановки 14, поступающего на вторые управляющие входы интеграторов 6, 7, 8 и 9 и индикатор 11. Сигналы с выходов интеграторов 6, 7, 8 и 9, которые в течение действия импульса на выходе формирователя импульсов остановки 14 постоянны во времени, подаются на соответствующие входы вычислительного блока 10, где происходит их перевод в цифровую форму и вычисление результата измерения по формуле (6). С выхода вычислительного блока 10 сигнал, являющийся результатом измерения, подается на индикатор 11, который фиксирует его и отображает до окончания следующего измерения.

Используемые в устройстве, реализующем предлагаемый способ, узлы могут быть построены следующим образом.

Перемножители и квадраторы могут быть построены по схемам логарифмических функциональных генераторов (У. Титце, К. Шенк. Полупроводниковая схемотехника. М. : Мир, 1982, с. 156). Интеграторы могут быть построены на основе операционных усилителей. Для обеспечения интегрирования в течение времени T_u применяются интеграторы с асинхронизацией и памятью. Схема такого интегратора приведена на стр. 144 в кн. У. Титце, К. Шенк. Полупроводниковая схемотехника. М.: Мир, 1982.

Индикатор может быть выполнен в виде последовательно включенных элемента выборки и хранения и стрелочного прибора. Элемент выборки и хранения можно реализовать на основе цифровых запоминающих устройств, а стрелочный прибор заменить на цифровой индикатор.

Формирователь импульса пуска может быть реализован по схеме синхронизируемого мультивибратора, а времязадающий элемент и формирователь импульсов остановки могут быть реализованы по схемам одновибраторов.

Вычислительный блок может быть реализован на основе микропроцессора Intel 80386 по типовой структуре с аналогоцифровыми преобразователями на входе.

Источник

Эта непостоянная постоянная составляющая: что делать?

Analog Devices AD822

Владимир Рентюк, Запорожье, Украина

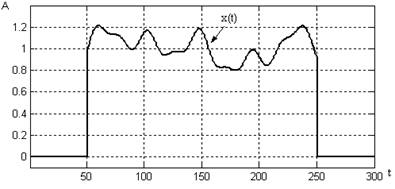
Ситуация, когда в полезном сигнале имеется постоянная составляющая, достаточно обычна. Эта составляющая может быть представлена некоторым фиксированным смещением или иметь нестационарный, плавающий характер. Как правило, она является паразитной и мешает производить обработку полезного переменного сигнала. Таким образом, возникает необходимость ее устранения, и обычно для этого используется разделительный конденсатор. Безусловно, это самое распространенное решение, и сразу вспоминается шутка, которой маститые инженеры вводят в ступор новичков, задавая им простой вопрос: как быстро доказать, что конденсатор проводит переменный ток и не пропускает постоянный. И на все их долгие и пространные объяснения показывают свое (Рисунок 1).

а) б)
Рисунок 1.	Конденсатор для напряжения постоянного и переменного токов. Постоянный ток «уперся» в конденсатор и дальше пройти не может (а), а переменный его «обходит» (б).

Если все изложенное является критичным, то на первый план выходит компенсация постоянной составляющей внешним смещением или задание строго необходимого при наличии некоторой постоянной составляющей в структуре сигнала. Подход хороший, но только если точно известно, какая она (постоянная составляющая) будет, и будет ли она постоянной. Причем, не только во времени, а и, в зависимости от внешних условий, как минимум, от температуры. Если не будет точной компенсации, то в случае, например, измерения среднеквадратичного значения сигнала, будет допущена ошибка. Еще один момент кроется в том, что если аналоговая часть, допустим некоторый масштабирующий усилитель, подключается на вход АЦП микроконтроллера, то для получения максимального динамического диапазона необходимо поднять аналоговый сигнал на величину напряжения, равную половине напряжения питания микроконтроллера или половине максимального номинального напряжения, допустимого для входа его АЦП.

Автору статьи пришлось однажды искать решение для, скажем так, «изделия специального назначения». В нем был блок обработки сигналов с большим динамическим диапазоном, поступающих с некого сенсора через систему сложных, переключаемых в зависимости от ситуации фильтров. Причем спектр этого сигнала достаточно широк, а его низкочастотная составляющая могла лежать в области инфранизких частот. Вычислитель осуществлял контроль среднеквадратичного уровня сигнала и при его отклонении в пределах ±1% выдавал некую очень важную команду. Кроме переменной составляющей, входной сигнал в своей структуре содержал еще и неизвестное по величине и меняющееся по уровню постоянное напряжение смещения. Вдобавок, на печатной плате не было лишнего места, и даже ее высота была ограничена, Ну и, коль это было «изделие специального назначения», то и требования к нему по ударо- и вибростойкости были специальные. Как видим, ни о каких разделительных конденсаторах или о подаче компенсирующего смещения речь даже не могла идти. Схемное решение, которое решило проблему такой необычной компенсации постоянной составляющей исходного сигнала (без разделительного конденсатора) и задания фиксированного и строго определенного смещения, приведено на Рисунке 2. Впервые в общем виде оно было опубликовано в [1].

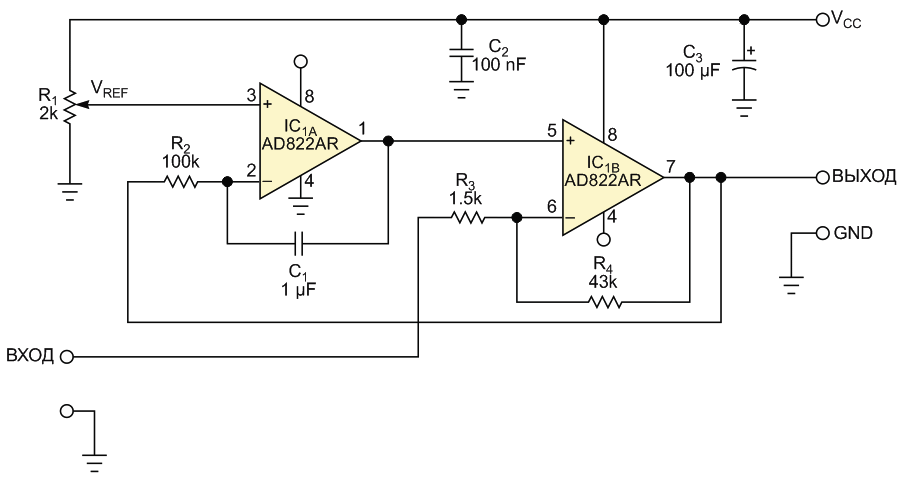Рисунок 2.	Схема цепи ультразвукового сенсора, использующая компенсацию постоянной составляющей входного сигнала [1].

Для предлагаемой схемы желательно использовать операционный усилитель (ОУ) типа «rail-to-rail» по входу и выходу, естественно, допускающий включение в режиме с однополярным источником питания, например, AD822 [2]. Это увеличивает динамический диапазон компенсации постоянной составляющей входного напряжения. Заданная величина выходного смещения, не зависящая от величины постоянной составляющей в структуре сигнала, устанавливается подачей необходимого уровня опорного напряжения V_REF. На Рисунке 2 он формируется при помощи построечного резистора R₁, но этот резистор может быть заменен источником опорного напряжения или резистивным делителем. (Автором успешно использовались оба варианта). Как уже отмечалось выше, для получения максимального динамического диапазона выходной уровень опорного постоянного напряжения устанавливается равным половине напряжения питания V_CC. Усилитель, выполненный на ОУ IC_1B, усиливает и инвертирует высокочастотную составляющую напряжения входного сигнала с коэффициентом усиления равным R₄/R₃, обычным для схем усилителей на базе ОУ в инвертирующем включении.

Инвертирующий вычитающий интегратор, выполненный на ОУ IC_1A, обеспечивает компенсацию любого неподходящего для работы схемы напряжения смещения внутри контура отрицательной обратной связи. Переменная составляющая сигнала ослабляется выбором соответствующей постоянной времени интегратора R₂C₁, оставляя, таким образом, лишь усредненную постоянную составляющую смещения на выходе ОУ IC_1B ниже нижней граничной рабочей частоты входного сигнала. Это смещение выходного сигнала в рабочем диапазоне частот будет равно заданному уровню опорного напряжения. На Рисунке 2 показана временная диаграмма действия такой компенсации для случая ступенчатого изменения смещения постоянной составляющей во входном сигнале на величину 4 В. То есть, если учитывать коэффициент усиления схемы, приведенной на Рисунке 2, равный

это будет в условиях очень глубокого перерегулирования, как минимум в 29 дБ! Тем не менее, и это можно видеть из Рисунка 3, время установления предлагаемой схемы с учетом переходных процессов составляет менее 100 мс.

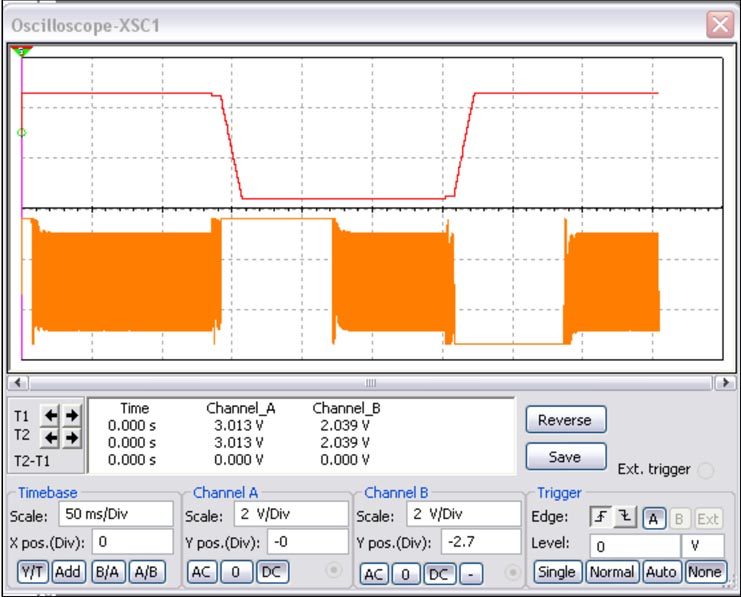Рисунок 3.	Процесс компенсации ступеньки смещения входного напряжения в 4 В. Время установления менее 100 мс.

Рассмотренное схемотехническое решение имеет еще две дополнительные полезные области применения. Во-первых, это ФВЧ первого порядка без входных емкостей, в котором амплитудно-частотная характеристика имеет спад 6 дБ/октава с частотой среза по уровню –3 дБ. Во-вторых, эта схема также может служить удобным в использовании дифференциатором (инвертирующим и без входного конденсатора) с реакцией на шаг ступенчатого изменения входного напряжения. Как известно, такие дифференциаторы являются потенциально неустойчивыми и, следственно, не очень удобны в применении.

Нижняя частота среза схемы, приведенной на Рисунке 2, определяется по формуле:

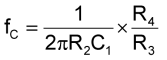(1)

Формула получена в результате моделирования. Для значений элементов, приведенных на Рисунке 2, частота среза в области низких частот равна 47 Гц.

А где же обещанные инфранизкие частоты, спросит читатель? Заменим элементы в интеграторе на R₂ = 2 МОм и C₁ = 2.2 мкФ и зададим коэффициент усиления, например, равный 12, то есть k = R₄/R₃ = 12. Это будет соответствовать той задаче, которую решал автор статьи в своем, упомянутом в начале статьи, проекте.

Согласно формуле (1), имеем:

АЧХ такого варианта каскада приведена на Рисунке 4.

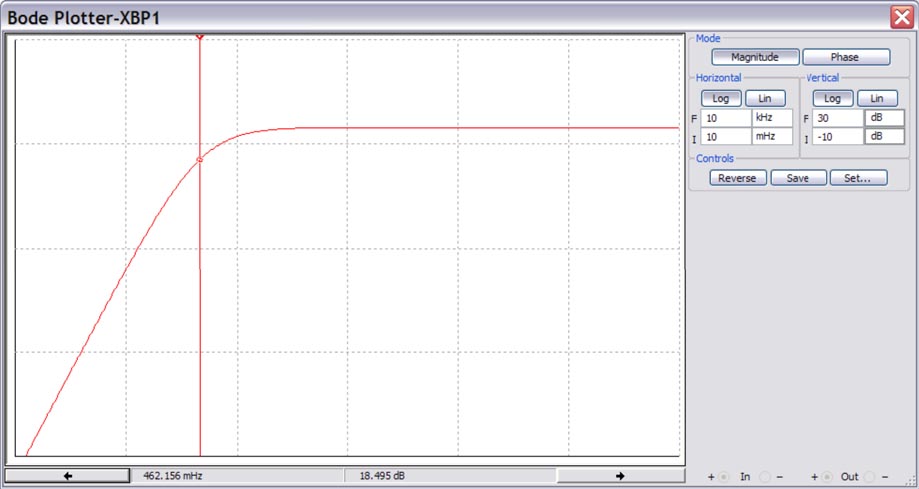Рисунок 4.	Амплитудно-частотная характеристика в области инфранизких частот.

Как видим, все обошлось без нежелательного разделительного электролитического конденсатора. В противном случае пришлось бы использовать электролитический конденсатор емкостью, как минимум, в 470 мкФ и, естественно, схему формирования сдвига выходного напряжения. Приведенное схемное решение было использовано автором в целом ряде проектов и ни разу не имело нареканий.

Ссылки:

Источник