Как изобразить графически комплексное число
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Как изобразить графически комплексное число
VII .1. Формы записи комплексных чисел и действия над ними
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
называются комплексно сопряженными.
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
, изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
можно записать в так называемой показательной (или экспоненциальной) форме
где r =| z | — модуль комплексного числа, а угол 
( k =0;–1;1;–2;2…).
Пример 7.1. Записать комплексные числа 
в тригонометрической и показательной формах.
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №39. Геометрическая интерпретация комплексного числа.
Перечень вопросов, рассматриваемых в теме
3) определение модуля комплексного числа.
а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке
Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Геометрическое изображение комплексных чисел.
а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).
Модуль комплексного числа
Как отмечалось выше, комплексное число также можно изображать радиус-вектором 
(рис. 4).
Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.
Иногда еще модуль комплексного числа обозначается как r или ρ.
Разбор решения заданий тренировочного модуля
№1. Тип задания: единичный выбор
Найдите модуль комплексного числа z=5-3i
Решим данное задание, используя определение модуля.
Верный ответ: 2. 
№2. Тип задания: рисование.
Изобразите вектором на комплексной плоскости точку z=2+3i
Разобьем z=2+3i на две части: z1=2 и z2= 3i. Отметим на плоскости точки О и А, соединим их:
Графическая форма представления комплексных чисел
Го ) числа.
2. Алгебраическая форма представления комплексных чисел
Комплексным числом или комплексом, называется число, состоящее из двух чисел ( частей ) – вещественного и мнимого.
Отрицательная единица называется мнимой и обозначается буквой «йот»:
j =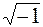 
(1 ).
Обозначим вещественное число в составе мнимого буквой “М”.
Тогда мнимое число можно записать так: j М. В таком случае, комплексное число А можно записать так:
Пример 1. Представить в алгебраической форме комплекс, вещественная часть которого равна 6, а мнимая 15.
Кроме алгебраической формы, комплексное число можно представить еще тремя:
Такое многообразие форм резко упрощает расчеты синусоидальных величин и их графическое изображение.
Поочередно рассмотрим графическую, тригонометрическую и показатель-
ную формы представления комплексных чисел.
Графическая форма представления комплексных чисел
Для графического представления комплексных чисел применяют прямо-
угольную систему координат. В обычной ( школьной ) системе координат вдоль осей «х» ( ось абсцисс ) и «y» ( ось ординат ) откладываются положительные или отрицательные вещественные числа.
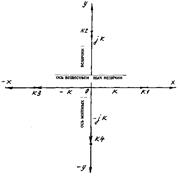
В системе же координат, принятой в символическом методе, вдоль оси «х»
в виде отрезков откладывают действительные числа, а вдоль оси «у» – мнимые
Рис. 1. Система координат для графического изображения комплексных чисел
Поэтому ось абсцисс «х» называют осью вещественных величин или, для сокращения, вещественной осью.
Ось ординат называют осью мнимых величин или мнимойосью.
Саму же плоскость ( т.е. плоскость рисунка ), на которой изображают комплексные числа или величины, называют комплекснойплоскостью.
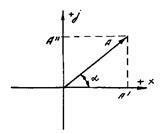
В этой плоскости комплексное число А = L + j М изображено вектором А
( рис. 2 ), проекция которого на вещественную ось равна его вещественной части Re A = А’ = L, а проекция на мнимую ось – мнимой части Im A = А» = М.
( Re – от англ. real – реальный, действительный, настоящий, Im – от англ.imaginary – нереальный, мнимый ).
Рис. 2. Графическое представление комплексного числа
В этом случае число А можно записать так
Используя графическое изображение числа А в комплексной плоскости, введем новые определения и получим некоторые важные соотношения:
1.длина вектора А называется модулем вектора и обозначается |A|.
По теореме Пифагора
2. уголα, образованный вектором А и вещественной положительной полу-
осью, называется аргументомвектора А и определяется через его тангенс:
tg α = А» / А’ = Im A / Re A ( 5 ).
Таким образом, для графического представления комплексного числа
А = А’ + А» в виде вектора надо:
1. найти модуль вектора |A| по формуле ( 4 );
2. найти аргумент вектора tg α по формуле ( 5);
3. найти угол α из соотношения α = arc tg α;
4. в системе координат j ( х ) провести под углом α вспомогательную
прямую и на ней в определенном масштабе отложить отрезок, равный модулю вектора |A|.
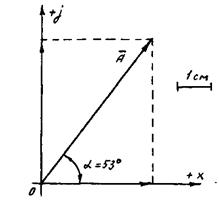
Пример 2. Комплексное число А = 3 + j 4 представить в графической форме.
|A| =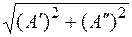 
= 
= 
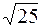
= 5
tg α = А» / А’ = 4 / 3 = 1, 33
3. угол α = arc tg α = arc 1,33 = 53º 03′ ≈ 53º
4. в системе координат j ( х ) проводим под углом α вспомогательную
Рис. 3. Комплексное число А = 3 + j 4, представленное в графическом виде
При необходимости из рис. 2 можно найти другие тригонометрические функции:
sin α = А» / |А|, отсюда А» = |А| sin α ( 6 )
cos α = А’ / |А|, отсюда А’ = |А| cos α ( 7 ).
Выражения ( 6 ) и ( 7 ) будут использованы ниже при объяснении тригоно-
метрического изображения комплексных чисел.
Дополним тему «Графическая форма представления комплексных чисел»
исследованием роли мнимой единицы при графическом изображении комплексных
Как изобразить графически комплексное число
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и называются комплексно сопряженными.
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число можно записать в так называемой показательной (или экспоненциальной) форме
где r =| z | — модуль комплексного числа, а угол ( k =0;–1;1;–2;2…).
Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах.
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.