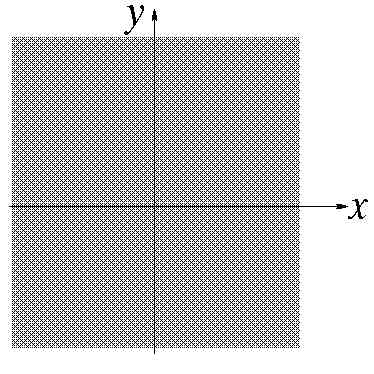
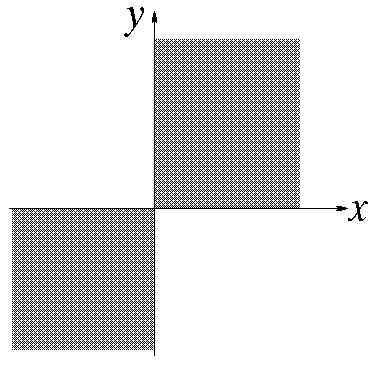
Как изобразить область истинности предиката

Логи­ка предикатов – это расширение логики высказываний за счет использова­ния предикатов в роли логических функций.

Например, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».

Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму «х – простое число». При одних значениях х (например, х = 13, х = 17) эта форма дает истинные высказывания, а при других значениях х (например, х = 10, х = 18) эта форма дает ложные высказывания.

Определение 1. Одноместным предикатом Р(х) называется всякая функция одного переменного, в которой аргумент x пробегает значения из некоторого мно­жества M, а функция при этом принимает одно из двух значений: истина или ложь.

Множество M, на котором задан предикат, называется областью определения предиката.

Множество , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).

Определение 2. Предикат Р(х), определённый на множестве M, называется тождественно истинным (тождественно ложным), если

Определение 3. Двухместным предикатом P(x, у) называется функция двух переменных х и у, определённая на множестве М=М₁×М₂ и принимающая значения из множества <1,0>.

В качестве примеров двухместных предикатов можно назвать предикаты: Q(x, у) – «х = у» предикат равенства, определённый на множестве R 2 =R×R; F(x, у) – «х || у» прямая х параллельна прямой у, определённый на множестве прямых, лежащих на данной плоскости.

Говорят, что предикат Р(х) является следствием предиката Q(х) , если ; и предикаты Р(х) и Q (х) равносильны , если .

Пример 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истин­ности:

Пусть на некотором множестве М определены два предиката Р(х) и Q(х).

Определение 4. Конъюнкциейдвух предикатов Р(х) и Q(х) называется новый предикат Р(х)&Q(х), который принимает значение «истина» при тех и только тех значениях , при которых каждый из предикатов Р(х) и Q(х) принимает значение «истина» и принимает значение «ложь» во всех остальных случаях. Очевидно, что областью истинности предиката Р(х)&Q(х) является общая часть областей истинности предикатов Р(х) и Q(х), т.е. пересечение .

Так, например, для предикатов Р(х): «х – четное число» и Q(х): « х кратно 3» конъюнкцией Р(х)&Q(х) является предикат «х – четное число и х кратно 3», то есть предикат «х делится на 6».

Определение 5. Дизъюнкцией двух предикатов Р(х) и Q(х) называется новый предикат , который принимает значение «ложь» при тех и только тех значе­ниях , при которых каждый из предикатов при­нимает значение «ложь» и принимает значение «исти­на» во всех остальных случаях. Ясно, что областью истинности предиката является объединение областей истинности предикатов Р(х) и Q(х), то есть объединение .

Определение 6. Отрицаниемпредиката Р(х) назы­вается новый предикат , который принимает значе­ние «истина» при всех значениях , при которых предикат Р(х) принимает значение «ложь», и принима­ет значение «ложь» при тех значениях , при кото­рых предикат Р(х) принимает значение «истина». Очевидно, что, .

Определение 7. Импликацией предикатов Р(х) и Q(х) называется новый предикат , который является ложным при тех и только тех значениях , при которых одновременно Р(х) принимает значение «истина», а Q(х) – значение «ложь» и принимает значе­ние «истина» во всех остальных случаях.

Ясно, что при выполнении логических операций над предикатами к ним применимы и равносильности алгеб­ры логики. Для детального изучения темы необходим курс «Дискретной математики».

Источник

MT1102: Линейная алгебра (введение в математику)

При изучении высказываний мы отмечали, что утверждение с переменными не является высказыванием. Можно, например, рассмотреть предложение %%P(x) : x^2 + 1 > 2%% с переменной %%x \in \mathbb R%%. Это предлождение не является высказыванием, так как нельзя сказать истинно оно или ложно. Однако, если заменить переменную %%x%% на какое-либо значение, например, %%x = 1%%, получаем высказывание %%2 > 2%%, которое является ложным. Заменив переменную %%x%% на значение %%x = 2%%, получим истинное высказывание %%5 > 2%%. Итак есть выражение %%P(x)%% не являющиееся высказыванием, но превращающееся в него при замене переменной %%x%% на ее произвольное значение из соответствующего множества.

Определение

Одноместным предикатом, определенным на множестве %%D%%, называется предложение с переменной, которое превращается в высказывание при замене этой переменной на ее значение из множества %%D%%. Одноместный предикат будем называть унарным или предикатом от одной переменной.

Примеры

Следующие предложения являются одноместными предикатами:

Следующие предложения не являются одноместными предикатами:

%%n%%-местный предикат

%%n%%-местым предикатом с областью определения %%D = D_1 \times D_2 \times \ldots \times D_n%% называется предикат %%P(x_1, x_2, \ldots, x_n)%% от %%n%% переменных, который превращается в высказывание при замене переменных %%x_1, x_2, \ldots, x_n%% на их значения из множеств %%D_1, D_2, \ldots, D_n%% соответственно.

Тогда предложение прямая %%x%% параллельна прямой %%y%% является двуместным предикатом %%P(x, y)%%, где %%X, Y%% — множество всех прямых.

Область определения предиката

Рассмотрим %%n%%-местный предикат %%P(x_1, x_2, \ldots, x_n)%%. В этом случае переменные берутся из множеств %%D_1, D_2, \ldots, D_n%% соответственно. Можно рассмотреть множество %%D = D_1 \times D_2 \times \ldots \times D_n%% — декартово произведение множеств %%D_1, D_2, \ldots, D_n%%, элементами которого являются всевозможные упорядоченные %%n%%-ки %%(d_1, d_2, \ldots, d_n)%% элементов исходных множеств.

Множество %%D%% называется областью определения предиката.

Область истинности

Пример

На множестве %%D = \< 1, 2, 3, 4, 5, 6, 7, 8, 9\>%% рассмотрим одноместный предикат %%P(x): x%% — простое число. Найти область истинности предиката %%P(x)%%.

Обозначим область истинности буквой %%A%%. Тогда %%A%% состоит из таких элементов, при которых выполняется предикат %%P(x)%%. Поэтому %%A = \<2, 3, 5, 7\>%%.

Операции над предикатами

Аналогично операциям для высказываний вводятся операции для предикатов.

Пусть %%P(x)%% и %%Q(x)%% — одноместные предикаты, определенные на множестве %%D%%.

Отрицанием предиката %%P(x)%% называется новый предикат, обозначаемый %%\overline%% и являющийся ложным для тех и только тех %%x%%, для которых предикат %%P(x)%% истинный.

Конъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) \land Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% истинны.

Дизъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) \lor Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% ложны.

Импликацией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) \rightarrow Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% истинный, а %%Q(x)%% ложный.

Эквиваленцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) \leftrightarrow Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% имеют одинаковые значения.

Применяя операции над предикатами, мы получаем составные предикаты, которые будем называть формулами алгебры предикатов.

Законы алгебры предикатов

В случае тождественно истинных и тождественно ложных предикатов имеем следующие определения.

Предикат %%P(x_1, x_2, \ldots, x_n)%% называется тождественно истинным если при любой замене переменных %%x_1, x_2, \ldots, x_n%% на их значения предикат превращается в истинное высказывание.

Предикат %%P(x_1, x_2, \ldots, x_n)%% называется тождественно ложным если при любой замене переменных %%x_1, x_2, \ldots, x_n%% на их значения предикат превращается в ложное высказывание.

Высказывание является частным случаем предиката, когда в предикате нет переменных. То есть высказывание является предикатом %%0%% порядка (от %%0%% переменных).

Источник

Предикаты и области истинности

Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

институт информационных наук и технологий безопасности

ФАКУЛЬТЕТ ЗАЩИТЫ ИНФОРМАЦИИ

ПРЕДИКАТЫ И ОПЕРАЦИИ НАД НИМИ. мНОЖЕСТВА ИСТИННОСТИ ПРЕДИКАТОВ. КВАНТОРЫ

студентов 2 курса направления подготовки

090900 «Информационная безопасность» (бакалавриат)

Предикаты и операции над ними.

Предика́т (n-местный, или n-арный) — это функция с множеством значений (или «ложь» и «истина»), определённая на множестве . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».

Предикат можно связать с математическим отношением: если (m₁,m₂. m_n) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.

Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.

Предикат называют тождественно-истинным и пишут:

если на любом наборе аргументов он принимает значение 1.

Предикат называют тождественно-ложным и пишут:

если на любом наборе аргументов он принимает значение 0.

Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.

Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры – конъюнкция, дизъюнкция, импликация и отрицание.

Примеры

Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y.

Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y», где множество M — это множество всех людей.

Операции над предикатами

Предикаты, так же, как высказывания, принимают два значения истинное и ложное, поэтому к ним применимы все операции логики высказываний. Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.

Логические операции

Конъюнкцией двух предикатов А(х) и В(х) называется новый предикат A(x)&B(x), который принимает значение «истина» при тех и только тех значениях Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката А(х)&В(х), является пересечение множеств истинности предикатов А(х) – Т₁ и В(х) – Т₂, т.е. Т = Т₁∩Т₂.

Пример: А(х): «х – четное число», В(х): « х кратно 3». А(х) В(х) – «х – четное число и х кратно 3». Т.е. предикат «х делится на 6».

Дизъюнкцией двух предикатов А(х) и В(х) называется новый предикат , который принимает значение «ложь» при тех и только тех значениях Т, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях. Областью истинности предиката является объединение областей истинности предикатов А(х) и В(х).

Импликацией предикатов А(х) и В(х) называется новый предикат 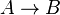, который является ложным при тех и только тех значениях Т, при которых А(х) принимает значение «истина», а В(х) – значение «ложь» и принимает значение «истина» во всех остальных случаях. Читают: «Если А(х), то В(х)».

Пример. А(х): «Натуральное число х делится на 3». В(х): «Натуральное число х делится на 4», можно составить предикат: «Если натуральное число х делится на 3, то оно делится и на 4». Множеством истинности предиката 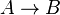является объединение множества Т2 – истинности предиката В(х) и дополнения к множеству Т1 истинности предиката А(х).

Предикаты и области истинности

Кроме высказываний, рассматриваются также высказывания с переменными, т.е. буквами, вместо которых можно подставлять определенные значения (например, числа). Если вместо всех переменных подставить их значения, то высказывание с переменными превратится в обычное высказывание.

Например, рассмотрим высказывание с переменной

.

—истинное высказывание,

— ложное высказывание.

Те наборы значений переменных, при которых получается истинное высказывание, образуют область истинности высказывания с переменными.

Определение. Предикат — это высказывание с переменными.

Пример. Область истинности предиката

— ;
предиката — ;
предиката :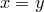

Область истинности предиката , где
— свободные переменные, — связанная переменная:

Область истинности предиката 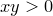(оси координат не включаем):

Область истинности предиката :

Если в предикаты P и Q входят одни и те же переменные, то область истинности предиката есть пересечение, а область истинности предиката — объединение областей истинности данных предикатов.

Кванторы

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

· Квантор всеобщности (обозначение: , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).

· Квантор существования (обозначение: , читается: «существует…» или «найдётся…»).

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

Примеры

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

1. любое натуральное число кратно 5;

2. каждое натуральное число кратно 5;

3. все натуральные числа кратны 5;

.

Следующие (уже истинные) высказывания используют квантор существования:

1. существуют натуральные числа, кратные 5;

2. найдётся натуральное число, кратное 5;

3. хотя бы одно натуральное число кратно 5.

Их формальная запись:

.

Высказывание означает, что область значений переменной включена в область истинности предиката .

(«При всех значениях (x) утверждение верно»).

Высказывание означает, что область истинности предиката непуста.

(«Существует (x), при котором утверждение верно»).

Дата добавления: 2018-02-15 ; просмотров: 5306 ; Мы поможем в написании вашей работы!

Источник