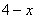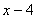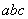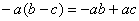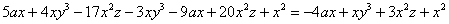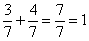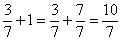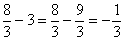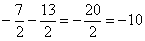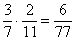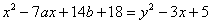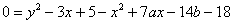Как изучать высшую математику самостоятельно

Математика с нуля

«Математика с нуля. Пошаговое изучение математики для начинающих» – это новый проект, предназначенный для людей, которые хотят изучить математику самостоятельно с нуля.

Сразу скажем, здесь нет лёгких решений и таких заявлений как «Купи эту книгу и сдай математику на 5» или «Освой математику за 12 часов» вы тут не увидите. Математика довольно большая наука, которую следует осваивать последовательно и очень медленно.

Сайт представляет собой уроки по математике, которые упорядочены по принципу «от простого к сложному». Каждый урок затрагивает одну или несколько тем из математики. Уроки разбиты на шаги. Начинать изучение следует с первого шага, и так далее по возрастанию.

Каждый изученный урок должен быть понятным. Поэтому, не поняв одного урока, нельзя переходить к следующему, поскольку каждый урок в математике основан на понимании предыдущего. Если вы с первого раза урок не поняли – не расстраивайтесь. Некоторые люди потратили месяцы и годы, чтобы понять хотя бы одну единственную тему. Отчаяние и уныние точно не ваш путь. Читайте, изучайте, пробуйте и снова пробуйте.

Математика хорошо усваивается, когда человек самостоятельно открыв учебник, учит самогó себя. При этом вырабатывается определенная дисциплина, которая очень помогает в будущем. Если вы будете придерживаться принципа «от простого к сложному», то с удивлением обнаружите, что математика не так уж и сложна. Возможно даже она покажется вам интересной и увлекательной.

Что даст вам знание математики? Во-первых, уверенность. Математику знает не каждый, поэтому осознание того, что вы знаете хоть какую-то часть этой серьёзной науки, делает вас особенным. Во-вторых, освоив математику, вы с лёгкостью освоите другие науки и сможете мыслить гораздо шире. Знание математики позволяет овладеть такими профессиями как программист, бухгалтер, экономист. Никто не станет спорить, что эти профессии сегодня очень востребованы.

В общем, дерзай друг!

Желаем тебе удачи в изучении математики!

Новые уроки будут скоро. Оставайся с нами!

Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Источник

Высшая математика для чайников, или с чего начать?

Нагромождение страшных формул, пособия по высшей математике, которые откроешь и тут же закроешь, мучительные поиски решения казалось бы совсем простой задачи…. Подобная ситуация не редкость, особенно когда учебник по математике последний раз открывался в далеком 11 классе. А между тем, в ВУЗах учебные планы многих специальностей предусматривают изучение всеми любимой высшей математики. И в этой ситуации нередко ощущаешь себя полным чайником перед нагромождением ужасной математической абракадабры. Причем, похожая ситуация может сложиться при изучении любого предмета, особенно из цикла естественных наук.

Что делать? Для студента-очника всё значительно проще, если, конечно, предмет не сильно запущен. Можно проконсультироваться у преподавателя, одногруппников, да и просто списать у соседа по парте. Даже полный чайник в высшей математике при таких раскладах сессию переживет.

А если человек учится на заочном отделении ВУЗа, и высшая математика, мягко говоря, в будущем вряд ли потребуется? К тому же совсем нет времени на занятия. Так-то оно, в большинстве случаев так, но никто не отменял выполнение контрольных работ и сдачу экзамена (чаще всего, письменного). С контрольными работами по высшей математике все проще, чайник ты, или не чайник – их можно заказать. И по остальным предметам тоже можно заказать. Но выполнение и сдача на рецензию контрольных работ еще не приведет к заветной записи в зачетной книжке. Часто бывает, что произведение искусства, выполненное на заказ, нужно защищать, и объяснить, почему из этих буковок следует вон та формула. Кроме того, предстоят экзамены, а там уже придется решать определители, пределы и производные САМОСТОЯТЕЛЬНО. Если, конечно, преподаватель не принимает ценные подарки, или нет нанятого доброжелателя за стенами аудитории.

Позвольте, дам очень важный совет. На зачетах, экзаменах по точным и естественным наукам ОЧЕНЬ ВАЖНО ХОТЬ ЧТО-ТО ПОНИМАТЬ. Запомните, ХОТЬ ЧТО-ТО. Полное отсутствие мыслительных процессов просто бесит преподавателя, мне известны случаи, когда студентов-заочников заворачивали по 5-6 раз. Помнится, один молодой человек сдавал контрольную работу 4 раза, и после каждой пересдачи обращался ко мне за консультацией. В конце концов, я заметил, что в ответе вместо буквы «пи» он писал букву «пэ», за что и последовали жесткие санкции со стороны рецензента. Студент ДАЖЕ НЕ ХОТЕЛ ВНИКАТЬ в задание, которое он небрежно переписал

Можно быть полным чайником в высшей математике, но крайне желательно знать, что производная константы равна нулю. Потому что, если Вы ответите какую-нибудь глупость на элементарный вопрос, то велика вероятность того, что на этом учеба в ВУЗе для Вас закончится. Преподаватели гораздо благосклоннее относятся к тому студенту, который ХОТЯ БЫ ПЫТАЕТСЯ разобраться в предмете, к тому, кто, пусть и ошибочно, но пробует что-либо решить, объяснить или доказать. И это утверждение справедливо для всех дисциплин. Поэтому следует решительно отмести позицию «я ничего не знаю, я ничего не понимаю».

Второй важный совет – ПОСЕЩАТЬ ЛЕКЦИИ, даже если их немного. Об этом я уже упоминал на главной странице сайта Математика для заочников. Повторяться нет смысла, почему это ОЧЕНЬ важно, читайте там.

Итак, что же делать, если на носу зачет, экзамен по высшей математике, а дела плачевны – состояние полного, а точнее говоря, пустого чайника?

Один из вариантов – нанять репетитора. С крупнейшей базой репетиторов можно ознакомиться здесь (преимущественно, Москва) или здесь (преимущественно, Санкт-Петербург). По поисковой системе вполне вероятно найти репетитора в своем городе, либо посмотреть местные рекламные газеты. Цена на услуги репетитора может варьироваться от 400 и более рублей за час в зависимости от квалификации преподавателя. Следует отметить, что дёшево – это не значит плохо, особенно если у Вас неплохая математическая подготовка. В то же время за 2-3К рублей Вы и получите НЕМАЛО. Зря таких денег никто не берёт, и напрасно таких денег никто не платит ;-). Единственный важный момент – старайтесь выбрать репетитора с профильным педагогическим образованием. И в самом деле, мы же не ходим за юридической помощью к стоматологу.

В последнее время набирает популярность сервис онлайн репетиторов. Он очень удобен, когда необходимо срочно решить одну-две задачи, разобраться в теме или подготовиться к экзамену. Безусловным преимуществом являются цены, которые в несколько раз ниже, чем у оффлайн репетитора + экономия времени на проезд, что особенно актуально для жителей мегаполисов.

В курсе высшей математики некоторые вещи без репетитора освоить весьма трудно, нужно именно «живое» объяснение.

Тем не менее, во многих типах задач вполне можно разобраться самостоятельно, и, цель данного раздела сайта – научить Вас решать типовые примеры и задачи, которые практически всегда встречаются на экзаменах. Более того, для ряда заданий существуют «жёсткие» алгоритмы, где от правильного решения вообще «никуда не деться». И, в меру моих знаний, я попытаюсь Вам помочь, тем более есть педагогическое образование и опыт работы по специальности.

Начнем разгребать математические абракадабры. Ничего страшного, даже если Вы чайник, высшая математика – это действительно просто и действительно доступно.

А начать нужно с повторения школьного курса математики. Повторение – мать мучения.

Прежде чем, Вы приступите к изучению моих обучающих материалов, да и вообще приступите к изучению любых материалов по высшей математике, НАСТОЯТЕЛЬНО РЕКОМЕНДУЮ, прочитать нижеследующее.

Для того чтобы успешно решать задачи по высшей математике НЕОБХОДИМО:

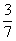
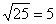
– Уметь складывать, вычитать, умножать и делить. Вспомнить, что любая дробь, например , обозначает деление, «три делить на семь» в данном случае. Вспомнить, что такое квадратный корень, например: .

ЗАПАСИТЕСЬ МИКРОКАЛЬКУЛЯТОРОМ. Оффлайновым. Это важно. Желательно, чтобы он был с функциями (синусами, логарифмами и т.д.) и умел считать обыкновенные дроби. Если его пока нет, пользуйтесь экселевскими калькуляторами проекта.

Кстати, Эксель. Отличный выбор и практически незаменимое приложение для решения многих задач! Мануал для «чайников» (пусть старенький) я загрузил в библиотеку.

– От перестановки слагаемых – сумма не меняется: .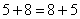
А вот это совершенно разные вещи:

Переставлять «икс» и «четверку» просто так нельзя. Заодно вспоминаем культовую букву «икс», которая в математике обозначает неизвестную или переменную величину.

– От перестановки множителей – произведение не меняется: .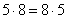
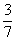
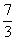
С делением такой фокус не пройдет, и – это две совершенно разные дроби и перестановка числителя со знаменателем без последствий не обходится.
Также вспоминаем, что знак умножения («точкy») чаще всего принято не писать: ,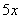

– Вспоминаем правила раскрытия скобок:
– здесь знаки у слагаемых не меняются
– а здесь меняются на противоположные.
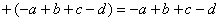
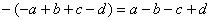
И для умножения: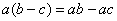

Вообще, достаточно помнить, что ДВА МИНУСА ДАЮТ ПЛЮС, а ТРИ МИНУСА – ДАЮТ МИНУС. И, постараться при решении задач по высшей математике в этом НЕ ЗАПУТАТЬСЯ (очень частая и досадная ошибка).

– Вспоминаем приведение подобных слагаемых, Вы должны хорошо понимать следующее действие:

– Вспоминаем что такое степень:

, , , .

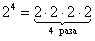
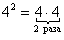
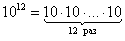
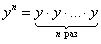
Степень – это всего лишь обычное умножение.

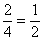
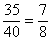
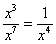
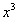
– Вспоминаем, что дроби можно сокращать: (сократили на 2), (сократили на пять), (сократили на ).

– Вспоминаем действия с дробями:

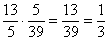
а также, очень важное правило приведения дробей к общему знаменателю: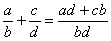

Если данные примеры малопонятны, смотрите школьные учебники.
Без этого ТУГО будет.

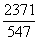
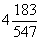
СОВЕТ: все ПРОМЕЖУТОЧНЫЕ вычисления в высшей математике лучше проводить в ОБЫКНОВЕННЫХ ПРАВИЛЬНЫХ И НЕПРАВИЛЬНЫХ ДРОБЯХ, даже если будут получаться страшные дроби вроде . Вот эту вот дробь НЕ НАДО представлять в виде , и, тем более, НЕ НАДО делить на калькуляторе числитель на знаменатель, получая 4,334552102….

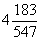
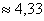
ИСКЛЮЧЕНИЕМ из правила является конечный ответ задания, вот тогда как раз лучше записать или .

– Уравнение. У него есть левая часть и правая часть. Например:

Можно перенести любое слагаемое в другую часть, сменив у него знак:
Перенесем, например, все слагаемые в левую часть: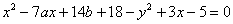

Или в правую:

Обратите внимание, что части уравнения можно безболезненно поменять местами: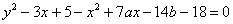
, рАвно, как и произвольно переставить слагаемые в пределах ОДНОЙ части.

– Правило пропорции:
(считаем, что отличны от нуля)

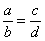
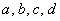
То, что находится внизу одной части – можно переместить наверх другой части.
То, что находится вверху одной части – можно переместить вниз другой части.

, , , , ,

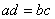
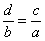
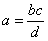
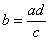
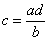
– И, наконец, стОит вспомнить о существовании некоторых функций, таких как, синус, косинус, тангенс, котангенс, логарифм.

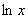
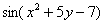
При этом в качестве аргумента функции может выступать не только буковка «хэ» (например, ), но и сложное выражение, например , и, рвать функцию на части категорически нельзя!

Не лишним будет вспомнить графики основных функций, предаться воспоминаниям можно на странице Графики и свойства элементарных функций. Там же освежаем в памяти актуальный технический вопрос – Как правильно построить график любой функции?

Кроме того, на складе математических формул и таблиц есть справочный материал Горячие формулы высшей математики.

И, наконец, через долгие-долгие годы я создал:

Кратчайший курс школьной математики

Где мы повторим именно то, что потребуется в высшей математике! Уникально кратко и уникально полезно! Доступна веб версия курса, а также pdf-книга.

Что дальше?

Дальше целесообразно изучить/повторить основы «трёх китов» высшей математики:

алгебры (статьи о множествах и уравнениях);

аналитической геометрии (вводный урок о векторах);

математического анализа (пределы, производные и упомянутая статья о графиках).

После чего можно смело приступать к другим урокам. Используйте левое навигационное меню и закомментированную карту сайта; почти все материалы расположены в логическом порядке их изучения. Также ориентируйтесь по ссылкам в статьях – как правило, я достаточно щепетильно (и даже занудно) останавливаюсь на том, что нужно знать и уметь для освоения той или иной темы.

И ещё одно важное напутствие: старайтесь выполнять ВСЕ предлагаемые мной задачи. Это не разрозненные примеры, а целостный и методически продуманный курс обучения, цель которого – НАУЧИТЬ.

С наилучшими пожеланиями, Александр Емелин

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Лекции и уроки по высшей математике

Карта сайта mathprofi.ru

Спокойно-спокойно – не удивляемся, такой «небоскрёб» «возведён» для удобства мобильных пользователей. Приветствую тех, кто зашёл на эту страничку с поисковика, меня зовут Емелин Александр и я рад представить вам свой курс высшей математики. Лекции и уроки носят практическую направленность и, кроме того, позволяют разобраться в теории. Поехали:

Если Вы хотите найти что-то конкретное, то имеет смысл сразу же воспользоваться поиском по сайту:

Поиск >>>

Не нашлось нужного материала?

Зайдите на страницу с тематическими архивами или посетите нашу библиотеку mathprofi.com, в которой можно раздобыть методички, лекции, контрольные, и др. учебные материалы.

Совсем-совсем дела плохи? Задайте вопрос на форуме!

Есть вопрос лично ко мне? Посмотрите часто задаваемые вопросы и если что – обращайтесь! Оставить свой отзыв можно в гостевой книге.

Для людей, начинающих изучать высшую математику, а также желающих восстановить свои знания/навыки предназначена организационная статья, которая так и называется:

Рекомендуемые математические ресурсы здесь >>>

Список доходчивой литературы здесь >>>

«Кладовка» со справочными материалами – здесь.

Кликаем по интересующему разделу и «спускаемся на лифте» к его подробному описанию! Все статьи в той или иной теме (и сами темы) я старался расположить в логической последовательности их изучения:

Аналитическая геометрия

Высшая алгебра

Пределы

Производная и некоторые её приложения

Функции и графики

Функции нескольких переменных

Однократные интегралы

Дифференциальные уравнения

Числовые ряды

Функциональные ряды

Кратные, криволинейные и поверхностные интегралы

Элементы векторного анализа

Комплексный анализ

Теория вероятностей

Я не хочу оформлять карту сайта «штабелем ссылок» и составляю её вручную, поэтому в настоящий момент здесь могут быть представлены не все темы. В том случае, если Вы не видите нужных разделов, пользуйтесь Поиском либо ориентируйтесь по левому навигационному меню, например, главной страницы

Аналитическая геометрия

В данном разделе можно выделить несколько блоков:

Векторы. «Альфа» и «омега» аналитической геометрии. Начинаем с двух базовых уроков:

и продолжаем следующими статьями:

Здесь наиболее трудной является 2-я лекция (о переходе) и поэтому я не рекомендую спешить с её изучением

Прямая на плоскости представлена следующими страницами:

Уравнение прямой на плоскости
Основные задачи с прямой на плоскости
Линейные неравенства
и Задача с треугольником, где я разбираю не только её, но вручаю вам «ключ» к решению многих задач по теме, да и не только по этой теме.

Линии второго порядка. Данный цикл лекций-уроков примечателен тем, что в него удалось ненавязчиво вместить значительное количество теории:

Полярная система координат. С ней целесообразно ознакомиться после изучения предыдущей темы, ибо окружностей и иже с ними тут хватает:

Полярные координаты – теоретические азы и простейшие примеры;
Практикум по построению типовых кривых в ПСК

И, наконец, геометрия пространства, где, наоборот – ярко выражена практика:

Высшая алгебра

Данный раздел также делится на несколько подразделов:

Вводные лекции, которые имеют огромное значение для изучения ВСЕГО курса высшей математики:

Комплексные числа. Любимая многими тема!

Комплексные числа для «чайников» – понятие и действия с числами;
Выражения уравнения и системы с комплексными числами – добротный и насыщенный практикум по теме.

Матрицы и определители. Уроки для «самых маленьких»:

и более серьёзные практические занятия:

Системы линейных алгебраических уравнений.

Опять же – базовый уровень:

Линейные преобразования. Собственно:

Линейные преобразования – интереснейшая и одна из самых важных лекций по алгебре, на которой я рассмотрел не только основы темы, но и обобщил понятие вектора.
Собственные числа и собственные векторы – наиболее известная и популярная задача.

Квадратичные формы. Держат нас в форме!

Понятие квадратичной формы, обычная и матричная запись, а также знакоопределенность и критерий Сильвестра;
Приведение формы к каноническому виду. Метод Лагранжа
Ортогональное преобразование квадратичной формы и геометрическое приложение – приведение уравнения линии 2 порядка данным методом.

Пределы

Пределы без предела =)

Базовые уроки для прожжённых гуманитариев:

и тотальный «разгром» лимитов для угорелых технарей:

+ более чем доступная лекция по теории, открывающая дверь в удивительный мир математического анализа:

Производная и некоторые её приложения

Как обычно – «песочница»:

и несколько уроков для отработки техники дифференцирования:

После чего целесообразно ознакомиться с теоретической лекцией Что такое производная? и потренироваться в нахождении производной по определению (нужно уметь находить пределы – см. выше)

И заключительная порция статей посвящена некоторым приложениям производной:

Уравнение нормали
Приближённые вычисления с помощью дифференциала (здесь волею судьбы оказалось рассмотрена и аналогичная задача для функции двух переменных)
Метод касательных

Функции и графики

Две справочно-прикладные статьи, без которых никуда! Причём во всей вышке:

Основной же цикл статей посвящён исследованию функции:

По материалам перечисленных уроков создан удобный справочный конспект:
Схема исследования функции

+ Нахождение наибольшего и наименьшего значений функции на отрезке
(самостоятельная задача и иногда «довесок» к полному исследованию)

Функции нескольких переменных

Один из предметов моей гордости – пожалуй, наиболее трудный в создании раздел. Его можно условно разделить на две части:

Область определения и линии уровня функции двух переменных – intro;
Основные поверхности пространства – не только справочная статья, но и ценное руководство по технике ручного построения поверхностей.

+ три «ласточки» на пределы и непрерывность:

Вторая часть раздела касается дифференцирования ФНП. Сначала отрабатываем технику решения:

после чего окончательно разбираемся в сути частных производных:

Производная по направлению и градиент – отличная лекция, не пропустите!

И наиболее распространённые приложения:

Однократные интегралы

В этот обширный раздел включены лекции-уроки о неопределенных, определённых и несобственных интегралах.

Неопределенные интегралы. Осваиваем «интегральный минимум студента»:

и укрепляемся на завоёванных рубежах:

Определённые интегралы. Тактика та же – изучаем вводную статью по теме + два «заштатных», но очень важных приложения:

Примерно здесь находится Рубикон раздела – знакомимся с лекцией, в которой я раскрыл суть интегрирования:

Несобственные интегралы представлены статьёй:

мануалом для более подготовленных читателей:

и темой для готовеньких:)

На следующих уроках закрепляем навыки решения интегралов:

И ставшие уже традиционными, статьи по численным методам. Как вычислить определённый интеграл приближённо:

Дифференциальные уравнения

Один из самых увлекательных и любимых мной разделов! Чего и вам желаю:

Сначала осваиваем основы темы и ДУ первого порядка.
Как повелось, «скорая помощь»:

а также незаменимый урок о линейных ДУ первого порядка.

И менее распространённые, но не менее важные:

После чего можно перейти к изучению следующего подраздела:

ДУ второго и высших порядков. Эти уравнения делятся на две «ветви»:

И на десерт:

Числовые ряды

Одна из самых простых и прозрачных тем:

Числовые ряды для «чайников» – понятие числового ряда и его сходимости, необходимый признак сходимости ряда, признаки сравнения;
Нахождение суммы ряда
Признак Даламбера, радикальный и интегральный признаки Коши
Знакочередующиеся ряды и признак Лейбница
+ Числовые ряды повышенной сложности – классифицированы!

Функциональные ряды

Для изучения этого раздела нужно освоить числовые ряды (см. выше).

Две статьи для «чайников»:

Ряды Фурье – в конце лекции есть много дополнительных материалов!

Кратные, криволинейные и поверхностные интегралы

Распространение идеи интегрирования на дву- и трёхмерные области.

Уроки по двойным интегралам:

Уроки по тройным интегралам:

Следующую тему изучаем не поверхностно:

А эту – не криво:)

Элементы векторного анализа

Захватывающая, но достаточно трудная тема, требующая знания, в частности криволинейных и поверхностных интегралов:

Основы теории поля – понятие скалярного и векторного поля, векторные линии, градиентное поле, ротор векторного поля, потенциальное поле;
Поток векторного поля, в том числе через замкнутую поверхность;
Дивергенция векторного поля и формула Гаусса-Остроградского
Циркуляция векторного поля и формула Стокса

Комплексный анализ

Статей пока немного, но они в тельняшках:

Рабочий справочный материал по двум нижеследующим статьям:
Таблица оригиналов и изображений

Теория вероятностей

Данную тему можно разделить на две большие главы

Случайные события

Случайные величины (СВ)

Здесь можно выделить три блока.

Дискретные случайные величины:

Непрерывные случайные величины:

Система случайных величин (двумерная случайная величина):

И будьте уверены:

(переход на главную страницу сайта)

Источник