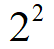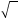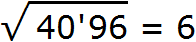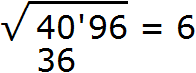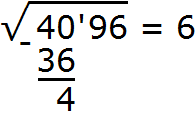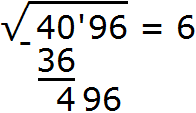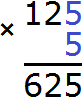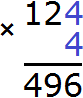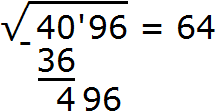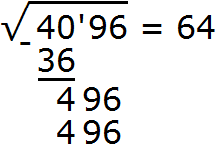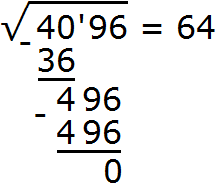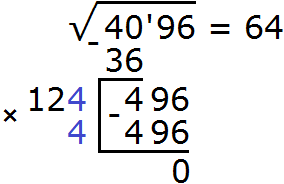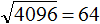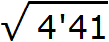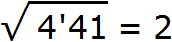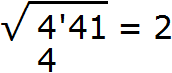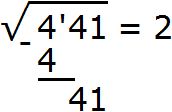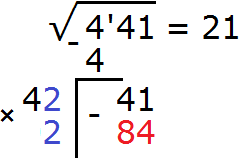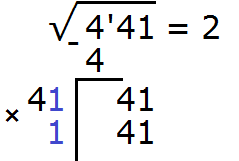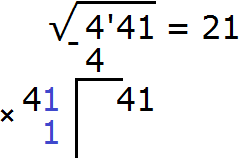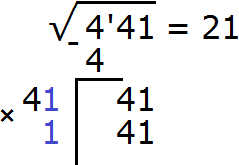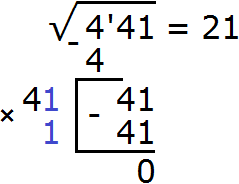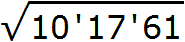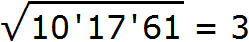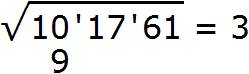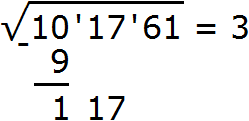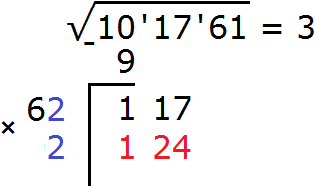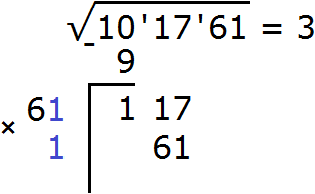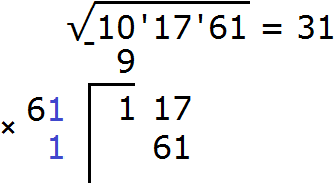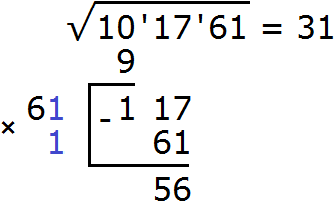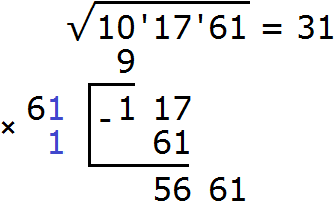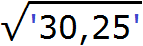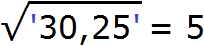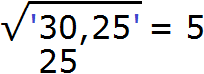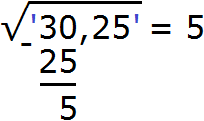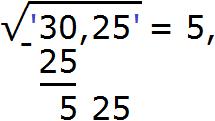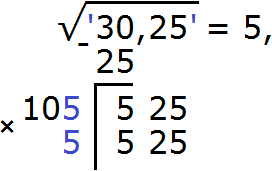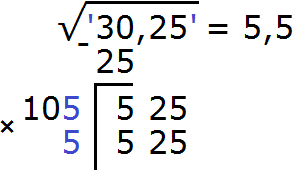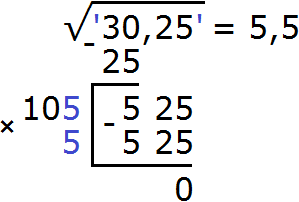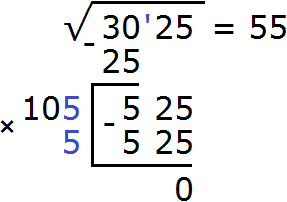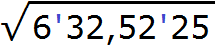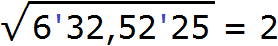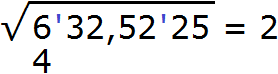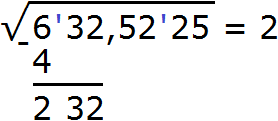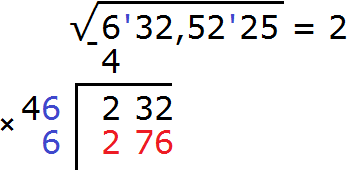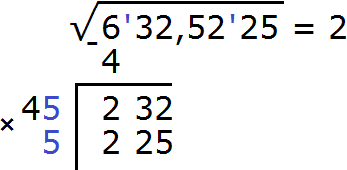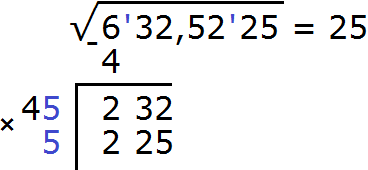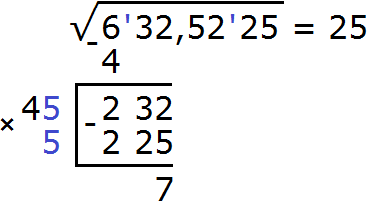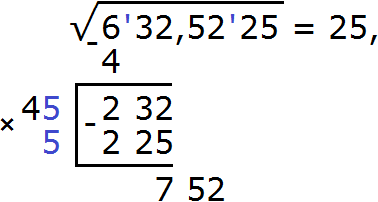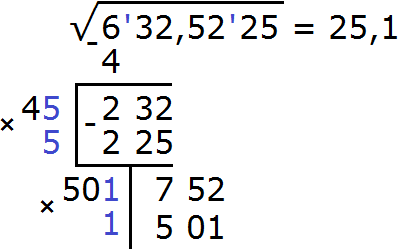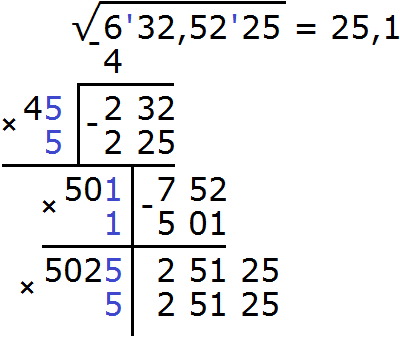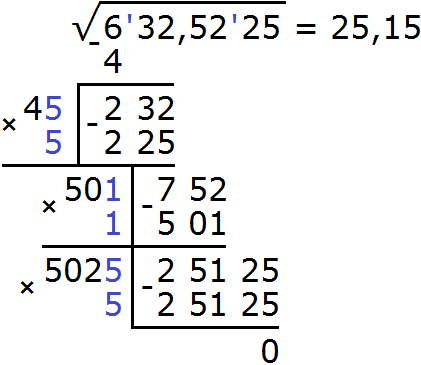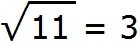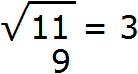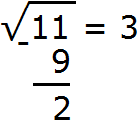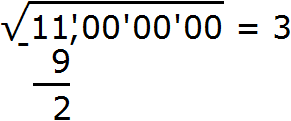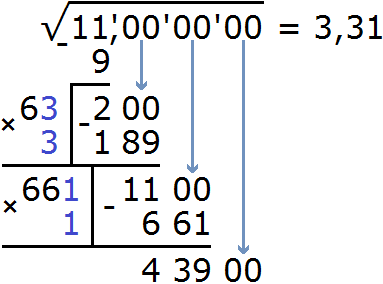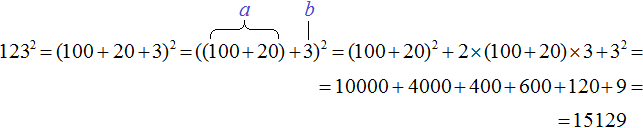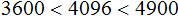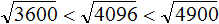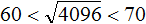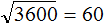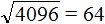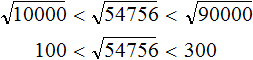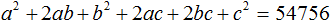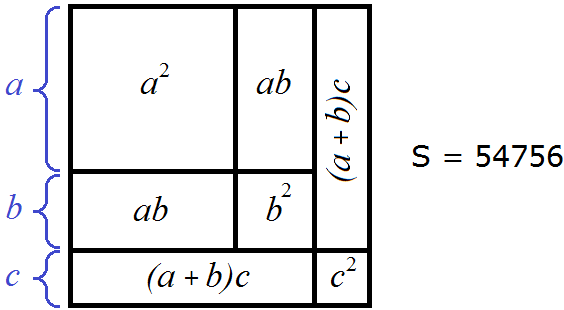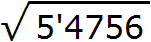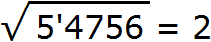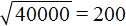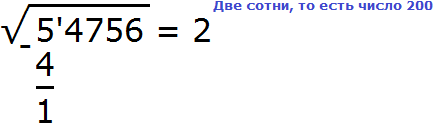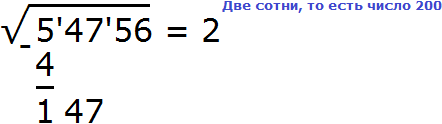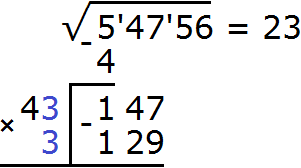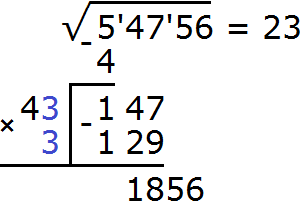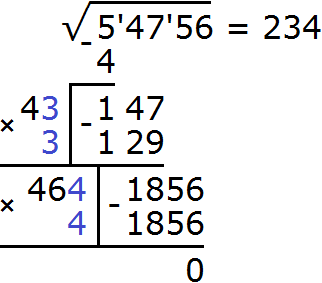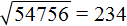Как извлечь квадратный корень числа
Вычислить квадратный корень из числа

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
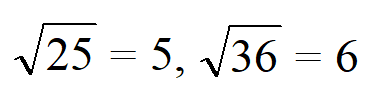
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 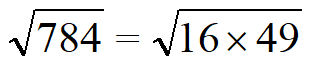 |
| Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 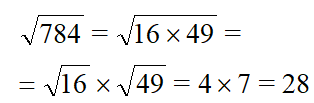 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 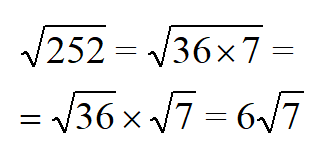 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76 7. |
| Вычисляем корень | 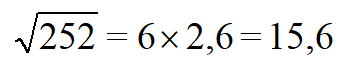 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. |  |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 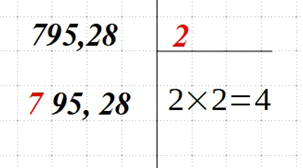 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 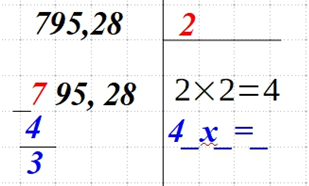 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 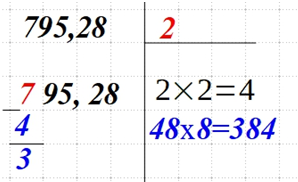 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 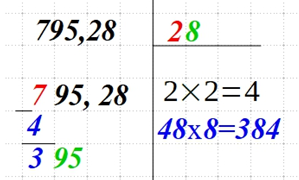 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 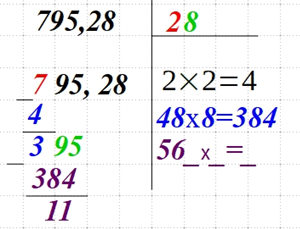 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 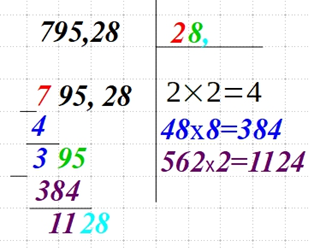 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 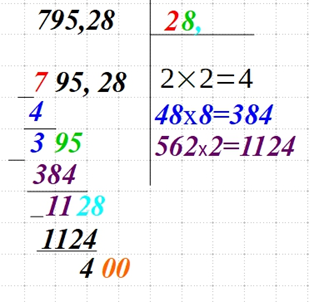 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
Алгоритм извлечения квадратного корня
Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня
Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.
Применение алгоритма может оказаться весьма полезным на контрольных и экзаменах. Ведь чаще всего на таких мероприятиях использовать калькулятор запрещено.
Как пользоваться алгоритмом
Рассмотрим применение алгоритма извлечения квадратного корня на конкретных примерах. О том, почему алгоритм следует применять именно так, поговорим позже.
Пример 1. Извлечём квадратный корень из числа 4096 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 4096 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку:
Сгруппированные цифры исходного числа называют грáнями, а саму группировку по две цифры разделением на грáни. Количество грáней позволяет предположить сколько цифр будет содержаться в извлечённом корне. В нашем примере извлечённый корень будет содержать две цифры, поскольку исходное число содержит две грани.
Теперь нужно извлечь квадратный корень из числа 40 с точностью до целых, получаем 6. Записываем 6 после знака равенства:
Далее возвóдим число 6 в квадрат и полученный результат записываем под числом 40
Далее вычитаем из числа 40 число 36, получаем 4. Записываем это число под 36
Снóсим оставшиеся цифры из под корня, а именно 96. Получаем остаток 496
Теперь нужно найти следующую цифру корня. Её находят так. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 496 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 12 и умножим образовавшееся число 125 на 5
Получилось число 625, которое больше остатка 496. Значит цифра 5 не годится в качестве следующей цифры корня. Проверим тогда цифру 4. Допишем ее к числу 12 и умножим образовавшееся число 124 на 4
Получилось число 496, которое в точности является нашим остатком. Значит дописанная к числу 12 цифра 4 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 4 в ответе после цифры 6
А число 496, которое получилось в результате умножения 124 на 4 записываем под остатком 496
Для удобства поиска второй цифры, слева от остатка проводят вертикáльную линию и уже за этой линией записывают умножение. В нашем случае умножение 124 на 4. Результат умножение сразу записывают под остатком:
Итак, квадратный корень из числа 4096 равен 64
Пример 2. Извлечём квадрáтный корень из числа 441 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 441 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку. В данном случае в числе 441 только три цифры. Поэтому группируем цифры 4 и 1. Крайняя четвёрка слева будет сама по себе:
Теперь нужно извлечь квадратный корень из числа 4 с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под числом 4
Вычитаем из числа 4 число 4, получаем 0. Ноль принято не записывать. Снóсим оставшиеся цифры корня, а именно 41
Теперь нахóдим следующую цифру корня. Первую найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 41 или хотя бы максимально близким ему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 4 и умножим получившееся число 42 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 41
Получилось число 41, которое в точности является нашим остатком. Значит дописанная к числу 4 цифра 1 является следующей цифрой корня. Записываем цифру 1 после цифры 2
А число 41, которое получилось в результате умножения 41 на 1, записываем под остатком 41
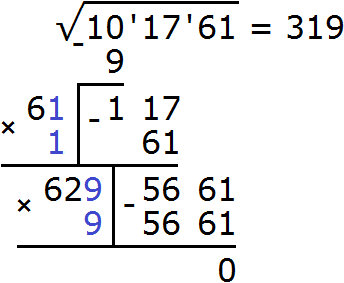
Пример 3. Извлечём квадратный корень из числа 101761 с помощью алгоритма извлечения квадратного корня.
Разбиваем число 101761 на грани:
Получилось три грани. Значит корень будет состоять из трёх цифр.
Извлекáем квадратный корень из первой грани (из числа 10) с точностью до целых, получаем 3. Записываем 3 после знака равенства:
Далее возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 10)
Вычитаем из числа 10 число 9, получаем 1. Снóсим следующую грань, а именно число 17. Получаем остаток 117
Теперь нахóдим вторую цифру корня. Первую найденную цифру корня, а именно 3 умножаем на 2, получаем 6. К числу 6 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 117 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 6 и умножим образовавшееся число 62 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 117
Получилось число 61, которое не превосходит остатка 117. Значит дописанная к числу 6 цифра 1 является второй цифрой корня. Записываем её в ответе после цифры 3
Снóсим следующую грань, а именно число 61. Получаем новый остаток 5661
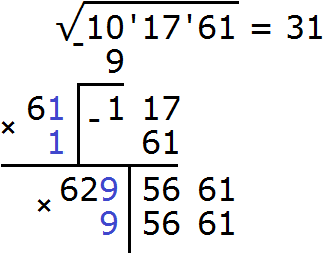
Теперь нахóдим третью цифру корня. Первые две найденные цифры корня, а именно число 31 умножаем на 2, получаем 62. К числу 62 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 9. Допишем её к числу 62 и умножим образовавшееся число 629 на ту же самую дописанную цифру 9. Результат умножения будем записывать сразу под остатком 5661
Получилось число 5661, которое в точности является нашим остатком. Значит дописанная к числу 62 цифра 9 является третьей цифрой корня. Записываем цифру 9 в ответе после цифры 1
Пример 4. Извлечём квадратный корень из числа 30,25 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. В данном случае на грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось по одной грани в каждой части. Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Извлечём квадратный корень из первой грани (из числа 30) с точностью до целых, получаем 5. Записываем 5 после знака равенства:
Далее возвóдим число 5 в квадрат и полученный результат записываем под первой гранью (под числом 30)
Вычитаем из числа 30 число 25, получаем 5.
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 30,25 с точностью до целых, получили ответ 5. Последний остаток 5 показывает, что целая часть 30 превосходит квадрат 5 2 на 5 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых), снесём следующую грань, а именно число 25, получим остаток 525. А в ответе после числа 5 следует поставить запятую, поскольку сейчас мы будем искать дробную часть корня.
Затем снóсим следующую грань, а именно число 25. Получаем остаток 525
Далее работаем по тому же принципу, что и раньше. Нахóдим следующую цифру корня. Для этого уже найденный корень, а именно число 5 умножим на 2 получим 10. К числу 10 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 525 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 10 и умножим получившееся число 105 на ту же самую дописанную цифру 5
Получилось число 525, которое в точности является нашим остатком. Значит дописанная к числу 10 цифра 5 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 5 после в ответе после запятой:
В подкоренном выражении можно было использовать следующий прием: умножить подкоренное число на 100 и получить под корнем число 3025. Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
Затем можно обратно разделить 3025 на 100 (или сдвинуть запятую влево на две цифры). В результате под корнем полýчится прежнее число 30,25, а правая часть уменьшится в десять раз и полýчится квадратный корень из числа 30,25.
Пример 5. Извлечём квадратный корень из числа 632,5225 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. Разбиваем число на грани. На грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось четыре грани. При этом две грани в целой части, и две грани в дробной. Это значит, что корень будет состоять из четырёх цифр: две цифры будет в целой части корня, и две цифры после запятой.
Извлечём квадратный корень из первой грани (из числа 6) с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под первой гранью (под числом 6)
Вычитаем из числа 6 число 4, получаем 2. Затем снóсим следующую грань, а именно число 32. Получаем остаток 232
Теперь нахóдим вторую цифру корня. Первую уже найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 232 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 4 и умножим получившееся число 46 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 232
Получилось число 225, которое не превосходит остатка 232. Значит дописанная к числу 4 цифра 5 является второй цифрой корня. Записываем её в ответе после цифры 2
Чтобы дальше извлечь корень (с точностью до десятых и сотых), снесём следующую грань, а именно число 52, получим остаток 752. А в ответе после числа 25 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
Далее работаем по тому же принципу, что и раньше. Нахóдим первую цифру корня после запятой. Для этого уже найденные цифры, а именно 25 умножим на 2 получим 50. К числу 50 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 752 или хотя бы максимально близким к нему, но не превосходящим его.
Теперь нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 502.
К числу 502 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 502 и умнóжим образовавшееся число 5026 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 25125
Получилось число 25125, которое в точности является нашим остатком. Значит дописанная к числу 502 цифра 5 является второй цифрой корня после запятой. Записываем цифру 5 в ответе после цифры 1
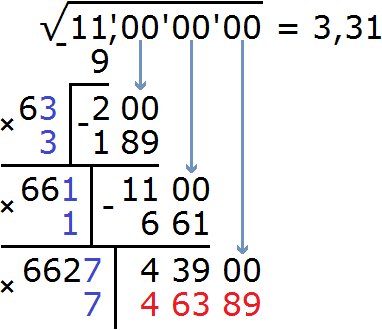
Пример 4. Используя алгоритм извлечения квадратного корня, извлечь квадратный корень из числа 11 с точностью до тысячных:
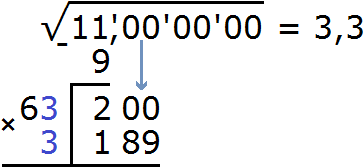
В данном числе только одна грань 11. Извлечём из неё корень с точностью до целых, получим 3
Теперь возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 11)
Выполним вычитание 11 − 9 = 2
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 11 с точностью до целых, получили ответ 3. Последний остаток 2 показывает, что целая часть 11 превосходит квадрат 3 2 на две квадратные единицы.
Наша задача была извлечь корень из числа 11 с точностью до тысячных. Значит нужно снести следующую грань, но её в данном случае нет.
Если после целого числа поставить запятую и написать сколько угодно нулей, то значение этого числа не измéнится. Так, после 11 можно поставить запятую и написать несколько нулей (несколько граней), которые в последствии можно будет снóсить к остаткам.
Если корень извлекáется с точностью до тысячных, то в ответе после запятой должно быть три цифры. Поэтому в подкоренном выражении поставим запятую и запишем три грани, состоящие из нулей:
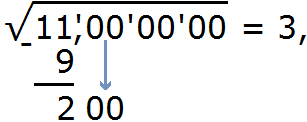
Теперь можно снести следующую грань, а именно два нуля. Получим остаток 200. А в ответе после числа 3 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
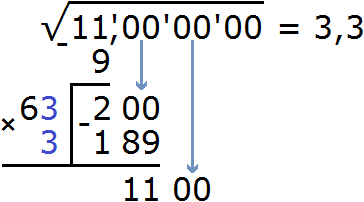
Теперь нахóдим первую цифру после запятой в ответе. Первую найденную цифру корня, а именно число 3 умножаем на 2, получаем 6. К числу 6 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 3
Выполним вычитание 200 − 189 и снесём следующую грань 00
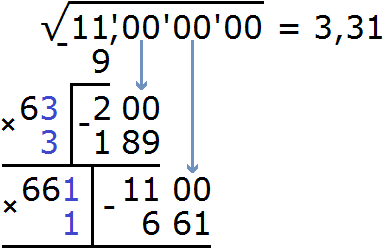
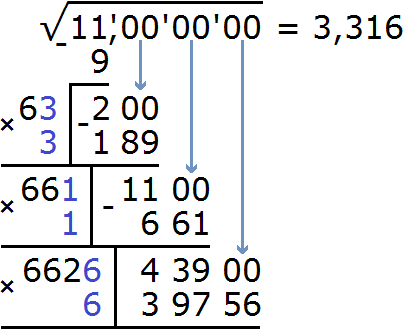
Нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 66.
К числу 66 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 1100 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 1
Выполним вычитание 1100−661 и снесём следующую грань 00
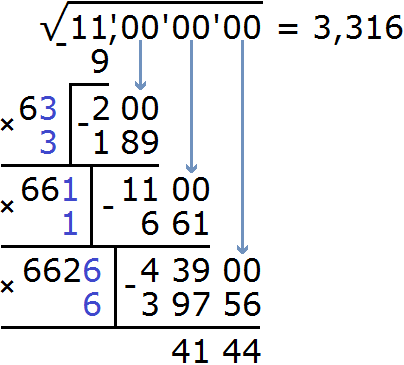
Нахóдим третью цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умножим на 2. Получим 662.
К числу 662 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 43900 или хотя бы максимально близким к нему, но не превосходящим его.
Получилось число 39756, которое не превосходит остатка 43900. Значит дописанная к числу 662 цифра 6 является третьей цифрой корня после запятой. Записываем цифру 6 в ответе после цифры 1
Выполним вычитание 43900 − 39756 = 4144
Дальнейшее вычисление не требуется, поскольку корень нужно было извлечь с точностью до тысячных.
Но в таких примерах как этот, цифры после запятой можно находить бесконечно. Например, так можно продолжить данный пример, найдя значение корня с точностью до десятитысячных:
Как работает алгоритм
Алгоритм извлечения квадратного корня основан на формуле квадрата суммы двух выражений:
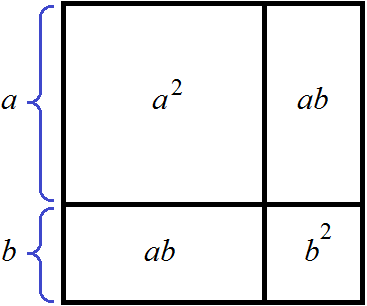
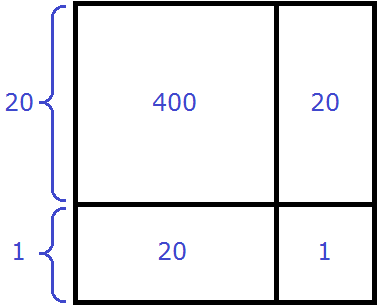
Геометрически эту формулу можно представить так:
Отметим, что формула квадрата суммы двух выражений позволяет возвести в квадрат любое число. Используя разряды, исходное число представляют в виде суммы чисел и далее эту сумму возвóдят в квадрат.
Например, так можно возвести число 21 в квадрат: представить данное число в виде суммы двух десятков и одной единицы, и далее эту сумму возвести в квадрат :
21 2 = (20 + 1) 2 = 20 2 + 2 × 20 × 1 + 1 2 = 400 + 40 + 1 = 441
Затем по отдельности вычисляются площади квадратов и прямоугольников, входящих в большой квадрат. А именно: один квадрат со стороной 20 (получается площадь, равная 400), два прямоугольника со сторонами 20 и 1 (получается две площади по 20), один квадрат со стороной 1 (получается площадь, равная 1). Результаты вычисления площадей складываются и получается итоговое значение 441.
Заметим также, что при возведéнии десятков в квадрат получились сотни. В данном случае при возведéнии числа 20 в квадрат получилось число 400. Это позволяет предположить, что если корень является двузначным числом, то десятки этого корня следует искать в сотнях подкоренного числа. Действительно, 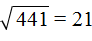
А при возведéнии сóтен в квадрат получаются десятки тысяч. Например, возведём в квадрат число 123, используя формулу квадрата суммы двух выражений. Число 123 это одна сотня, два десятка и три единицы:
123 2 = (100 + 20 + 3) 2
При изучении многочленов мы выяснили, что если многочлен содержит более двух членов и возникла необходимость применить формулу квадрата суммы, то некоторые из членов можно взять в скобки, чтобы получилось выражение вида (a + b) 2
Рассмотрим подробное извлечение квадратного корня из числа 4096. Заодно пройдёмся по основным этапам алгоритма извлечения квадратного корня, рассмотренного в предыдущей теме.
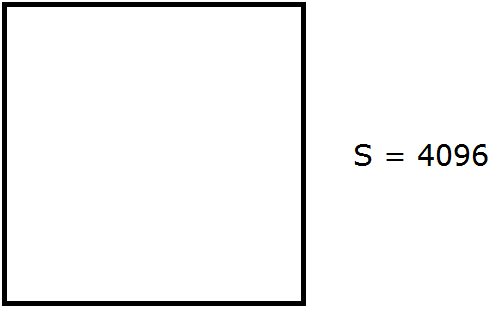
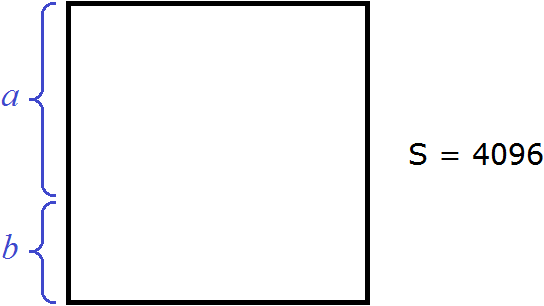
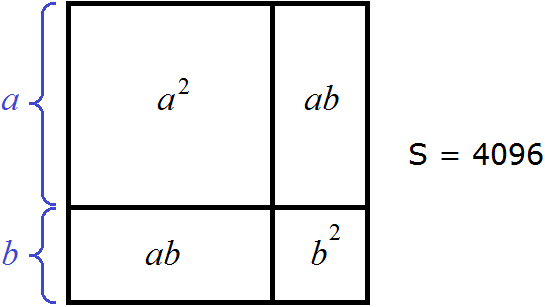
Допустим, что число 4096 это площадь следующего квадрата:
Извлечь корень из числа 4096 означает найти длину стороны данного квадрата:
Запишем каждое число под знáком корня:
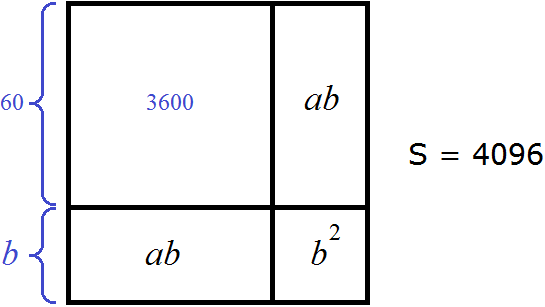
Квадратные корни из чисел 3600 и 4900 нам известны. Это корни 60 и 70 соответственно:
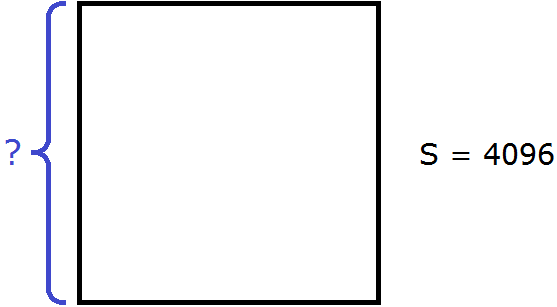
Корни 60 и 70 являются двузначными числами. Если квадратный корень из числа 4096 располагается между числами 60 и 70, то этот корень тоже будет двузначным числом.
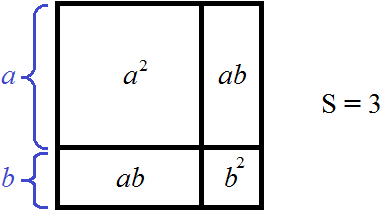
Тогда сторона квадрата будет разбита на две составляющие: a и b
Перепишем в равенстве (a + b) 2 = 4096 левую часть в виде a 2 + 2ab + b 2
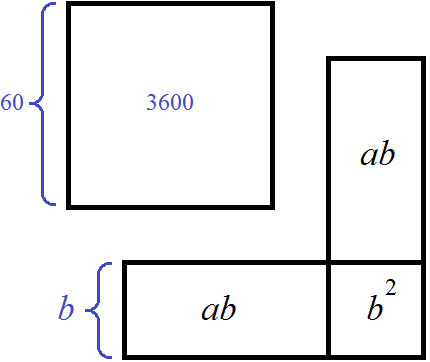
Тогда рисунок, иллюстрирующий квадрат площадью 4096, можно представить так:
Вернёмся к извлечению корня. Мы выяснили, что корнем будет двузначное число. Двузначное число состоит из десятков и единиц. При возведéнии десятков в квадрат, получаются сотни. Тогда десятки искомого корня следует искать в сотнях подкоренного числа. В подкоренном числе 40 сотен. Отделим их небольшой помéткой:
Извлечём корень из числа 40. Из числа 40 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых.
Ближáйший мéньший квадрат к числу 40 это 36. Извлечём корень из этого квадрата, получим 6. Тем сáмым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 40, а из сорокá сотен. Метка, которая постáвлена после числа 40, отделяет разряды числа, находящегося под знáком корня. Нужно понимать, что в данном случае 40 это 4000.
Из 4000 как и из 40 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 4000. Но нужно принимать во внимание следующий момент. Десятки это числа с одним нулем на конце. Примеры:
120 — двенадцать десятков
При возведéнии таких чисел в квадрат, получаются числа с двумя нулями на конце:
Но ранее в ответе мы написали не 60, а 6. Это является сокращённым вариантом. Число 6 в данном случае означает шесть десятков:
Итак, десятки корня найдены. Их шесть. Теперь нужно найти единицы корня. Единицы корня это длина оставшейся маленькой стороны квадрата, то есть значение переменной b.
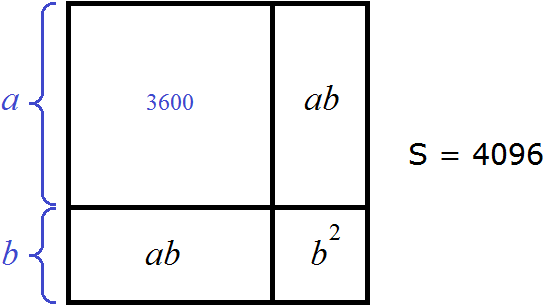
На рисунке видно как из квадрата, площадь которого 4096 отделился квадрат, площадь которого 3600. Осталась фигура, площадь которой 496.
Именно поэтому в процессе применения алгоритма первая найденная цифра корня возводится в квадрат, чтобы результат возведения вычесть из сотен подкоренного выражения.
Так, из 40 сотен вычитаются 36 сотен, остаётся 4 сотни плюс сносятся девяносто шесть единиц. Эти четыре сотни и девяносто шесть единиц вместе образуют 496 единиц:
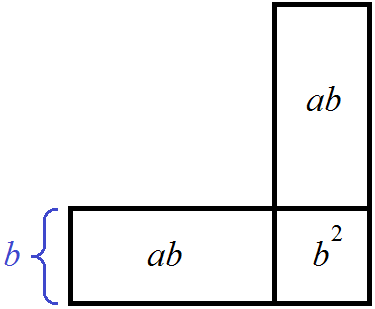
Оставшаяся фигура есть ни что иное как удвоенное произведение первого выражение a плюс квадрат второго выражения b
Значение a уже известно. Оно равно 60. Тогда равенство примет вид:
Но для удобства поиска этой цифры, переменную b выносят за скобки. Вернёмся к выражению 120b + b 2 = 496 и вынесем b за скобки:
Именно поэтому при использовании алгоритма, уже найденную цифру умножают на 2. Так, 6 мы умножили на 2 получили 12 и уже к 12 дописывали цифру и умножáли образовавшееся число на ту же дописанную цифру, пытаясь получить остаток 496.
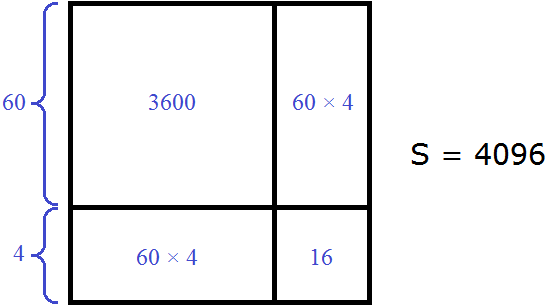
Если из общей площади вычесть 3600, затем 496, полýчим 0. Остаток, равный нулю, говорит о том, что решение завершено:
4096 − 3600 − 496 = 0
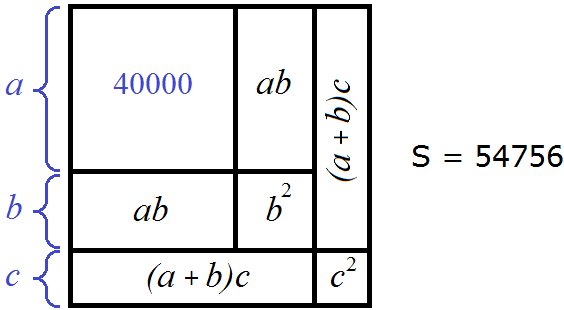
Пример 2. Извлечь квадратный корень из числа 54756
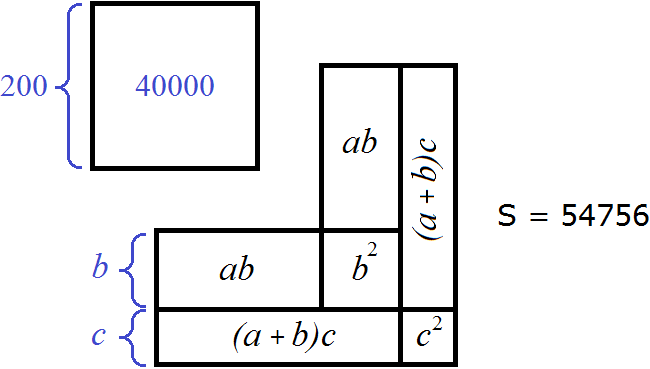
Пусть число 54756 это площадь следующего квадрата:
Извлечь корень из числа 54756 означает найти длину стороны данного квадрата:
Пока неизвестно является ли квадратный корень из числа 54756 целым либо дробным числом. Узнáем для начала из скольких цифр будет состоять целый корень.
Корни из 10000 и 90000 являются трёхзначными числами.
Тогда корень из 54756 тоже будет трёхзначным числом. А трёхзначное число состоит из сотен, десятков и единиц.
Выполним в левой части равенства (a + b + c) 2 = 54756 возведéние в квадрат:
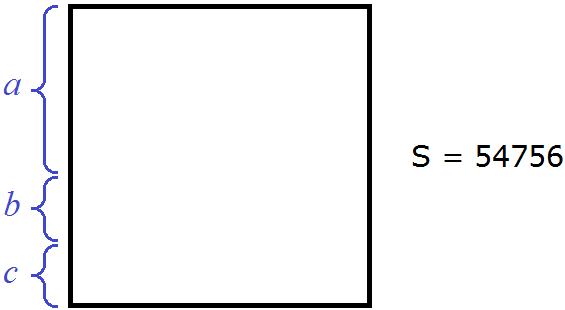
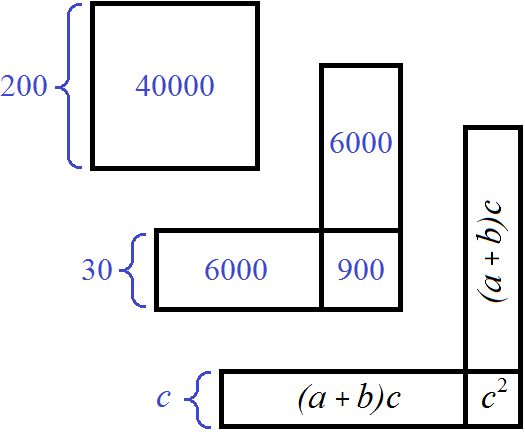
Тогда рисунок иллюстрирующий квадрат, площадью 54756 можно представить так:
Вернёмся к извлечению корня. Мы выяснили, что корнем будет трёхзначное число. Трёхзначное число состоит из сотен, десятков и единиц.
При возведéнии сотен в квадрат, получаются десятки тысяч. Тогда сотни искомого корня следует искать в десятках тысяч подкоренного числа. В подкоренном числе 5 десятков тысяч. Отделим их мéткой:
Извлечём корень из числа 5. Из числа 5 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых Ближáйший мéньший квадрат к 5 это 4. Извлечём корень из этого квадрата, получим 2. Тем самым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 5, а из пяти десятков тысяч. Метка, которая поставлена после числá 5, отделяет разряды числá, находящегося под знáком корня. Нужно понимать, что в данном случае 5 это 50000.
Из 50000 как и 5 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 50000. Но нужно принимать во внимание, что сотни это числа с двумя нулями на конце. Примеры:
При возведéнии таких чисел в квадрат, получаются числа, у которых четыре нуля на конце:
Мы ищем сотни корня в десятках тысяч числа 54756, то есть в числе 50000. Но нет такого числá с двумя нулями на конце, вторая степень которого равна 50000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с четырьмя нулями на конце. Таковым является квадрат 40000.
Теперь извлечём корень из квадрата 40000
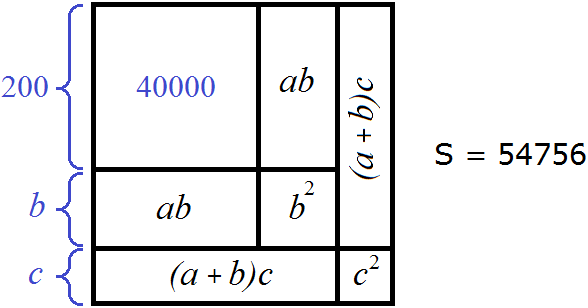
Итак, мы нашли сторону квадрата, площадь которого 40000. Подпишем сторону a как 200
Теперь вытаскиваем остаток. Из пяти десятков тысяч корень извлечён только из четырёх десятков тысяч. Значит в остатке остался один десяток тысяч. Вытащим его:
Десятки в квадрате составляют сотни. Поэтому десятки корня следует искать в сотнях подкоренного числа. Под корнем сейчас 47 сотен. Снесём их к остатку 1, предварительно отделив их под корнем мéткой:
Один десяток тысяч это сто сотен, плюс снесено 47 сотен. Итого 100 + 47 = 147 сотен. В эти 147 сотен должна входить сумма 2ab + b 2
Переменная a уже известна, она равна 200. Подставим это значение в данное равенство:
2 × 200 × b + b 2 = 14700
400b + b 2 = 14700
Теперь наша задача найти такое значение b, при котором левая часть станет равна 14700 или хотя близкой к этому числу, но не превосходящей его. Поскольку b является десятками искомого корня, то значение b является двузначным числом с одним нулём на конце. Такое число можно найти методом подбора. Для удобства вынесем в левой части за скобки b
Теперь левую часть можно понимать так: к 400 следует прибавить некоторое число b, которое при умножении с тем же самым b даст в результате 14700 или близкое к 14700 число, не превосходящее его. Подставим например 40
17600 ≠ 14700
Получается 17600, которое превосходит число 14700. Значит число 40 не годится в качестве десятков корня. Проверим тогда число 30
Теперь вытаскиваем остаток. В 147 сотен вместилось только 129 сотен. Значит в остатке осталось 147 − 129 = 18 сотен плюс сносим число 56 из подкоренного выражения. В результате образýется новый остаток 1856
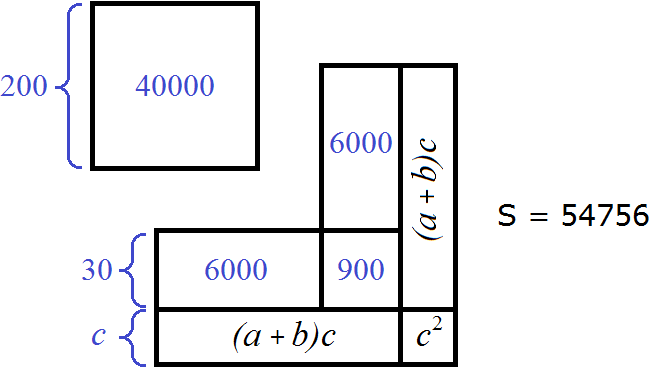
Переменные a и b уже известны, они равны 200 и 30 соответственно. Подставим эти значения в данное равенство:
2(200 + 30)c + c 2 = 1856
2 × 230c + c 2 = 1856
54756 − 40000 − 6000 − 6000 − 900 − 920 − 920 − 16 = 0
Пример 3. Извлечь квадратный корень из числа 3
Квадратный корень из числа 3 не извлекается. Ранее мы говорили, что квадратные корни из таких чисел можно извлекать только приближённо с определенной точностью.
Пусть 3 это площадь следующего квадрата:
Извлечь корень из числа 3 значит найти длину стороны данного квадрата:
Корень из 3 больше корня из 1, но меньше корня из 4
Корни из 1 и 4 являются целыми числами.
Между числами 1 и 2 нет целых чисел. Значит корень из числа 3 будет десятичной дробью. Найдём этот корень с точностью до десятых.
Выполним в левой части данного равенства возведéние в квадрат:
Тогда рисунок, иллюстрирующий квадрат площадью 3, можно представить так:
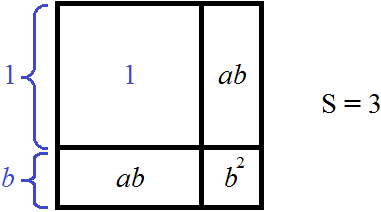
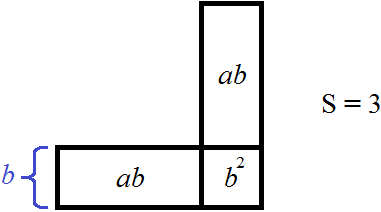
Если a 2 это 1, а площадь всего квадрата равна 3, то в остатке останется 2. В этот остаток должна вмещаться площадь оставшейся фигуры:
Значение a уже известно, оно равно единице:
Вынесем за скобки b
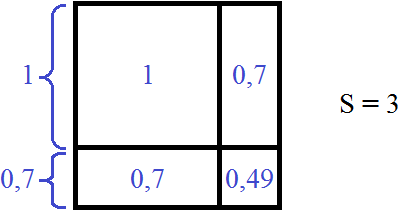
Получилось 1,89 которое приближённо равно 2 и не превосходит его. Значит 0,7 является значением b
Значит квадратный корень из 3 с точностью до десятых приближённо равен 1 + 0,7
К сожалению, понять механизм алгоритма извлечения квадратного корня намного сложнее, чем использовать сам алгоритм. Решите несколько примеров на применение алгоритма, и понимание механизма его работы будет даваться вам значительно проще.
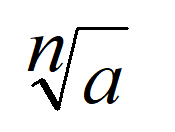
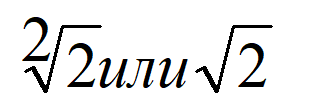
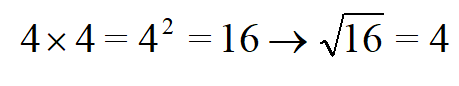
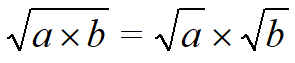
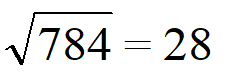
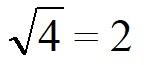
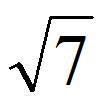 между 2 и 4.
между 2 и 4.