Как извлекать корень третьей степени
Кубический корень (извлечение без калькулятора)
Кубический корень. Как извлечь квадратный корень из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в Задаче 27125 требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
Простые и не очень способы того, как вычислить кубический корень
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
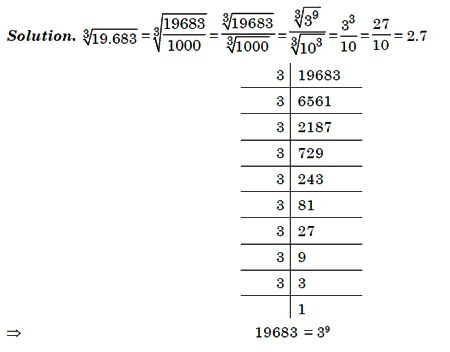
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
Извлечение корней: методы, способы, решения
Из этой статьи вы узнаете:
Что такое «извлечение корня»
Для начала введем определение «извлечение корня».
Извлечение корня — процесс нахождения значения корня.
Выражения «извлечение корня» и «нахождение значения корня» равнозначны.
В каких случаях извлекается корень?
Принципы нахождения значения корня и способы их извлечения
Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.
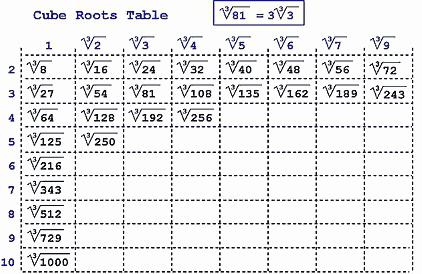
Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.
Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).
Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.
Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.
И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.
Использование таблицы квадратов, кубов и т.д.
Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.
Таблица квадратов
| Таблица квадратов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.
Таблица кубов
| Таблица кубов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 | ||
Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.
Разложение подкоренного числа на простые множители
Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.
Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.
Разложим 144 на простые множители:
Также при использовании свойств степени и корней можно записать преобразование немного по-другому:
144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12
Извлечение корней из дробных чисел
Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.
Следуя свойству корня из частного, справедливым является следующее равенство:
Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.
Извлечение корня из отрицательных чисел
Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
Затем следует заменить смешанное число обыкновенной дробью:
Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:
Вычисляем корни в числителе и знаменателе:
Краткая запись решения:
Поразрядное нахождение значения корня
В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.
| Возможное значение корня | 2,0 | 2,1 | 2,2 | 2,3 |
| Это значение в степени | 4 | 4,41 | 4,84 | 5,29 |
| Возможное значение корня | 2.20 | 2,21 | 2,22 | 2,23 | 2,24 |
| Это значение в степени | 4,84 | 4,8841 | 4,8294 | 4,9729 | 5,0176 |
Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.
Корни и степени
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
Определим также, что такое степень с целым отрицательным показателем.
Заметим, что при возведении в минус первую степень дробь переворачивается.
Свойства арифметического квадратного корня:
Кубический корень
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Сразу договоримся, что основание степени больше 0.
При этом также выполняется условие, что больше 0.
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Корень 3-й степени или КУБИЧЕСКИЙ КОРЕНЬ из числа A определяется как такое число B, что B 3 = A. То есть куб числа B равен А. Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат).
Результат
Кубический корень из числа равен:
Другие калькуляторы:
Корень n-й степени из числа A есть решение X уравнения x n = A (отметим, что решений может быть несколько или ни одного)
Корень нечётной степени из положительного числа — положительное число, однозначно определенное.
Корень нечётной степени из отрицательного числа — отрицательное число, однозначно определенное.
Корень любой натуральной степени из нуля — ноль.
Для того, чтобы упростить любой корень, необходимо разложить подкоренное выражение на простые множители и вынести за знак корня тот множитель, который повторяется равное степени корня число раз.
Видео
Подробно про кубический корень можно узнать из видео:
Примеры
Задание: Извлечь корень 3 степени из числа 27
Решение: Пользуемся калькулятором, результат = 3
Задание: Посчитать кубический корень из 64:
Решение: Пользуемся онлайн расчетом, получается 4
Задание: Посчитать корень третьей степени из числа 8:
Решение: Корень третьей степени из числа 8 равен 2