Как картографические проекции отображают земную поверхность
Картографические проекции. Урок 6
Картографические проекции сегодня – это математические способы изображения всего земного эллипсоида или его части на плоскости, систематическое преобразование широт и долгот с поверхности сферы на плоскость.
Для создания географических карт выполняют две последовательных операции:
При этом картографы пытаются добиться как можно меньшего количества искажений. Сделать мелкомасштабную карту совсем без искажений невозможно. На крупномасштабных (топографических) картах искажения почти отсутствуют. В зависимости от назначения карты одни погрешности допустимы, другие нет. Поэтому и существуют разные типы проекций, предназначенные для сохранения некоторых свойств сферы за счёт других её свойств.

Виды искажений при использовании картографических проекций
Разложить на плоскости эллипс или шар очень трудно, для того, чтобы убедиться в этом, можно попробовать это сделать на практике. Сложить кусочки апельсиновой кожуры так, чтобы между ними не было пустых мест и попробовать получить непрерывную ровную плоскость. Корка соберётся в складки, она не уложится без промежутков.
При любом способе разложения шара на плоскость присутствует один или несколько типов искажения:
При этом типы искажений взаимозависимы, при уменьшении одного из показателей увеличивается другой. В зависимости от назначения карты, на ней присутствуют места с нулевым искажением, с удалением от него количество искажений увеличивается. Поэтому на карте есть три вида масштаба:
При выборе типа картографической проекции сначала строят изоколы – изолинии, соединяющие точки с одинаковым искажением.

Источник: https://ds04.infourok.ru/uploads/ex/0617/00148bfe-04623ef1/hello_html_329bd6b7.jpg
Типы проекций по характеру искажений
Для разных целей нужны карты с отсутствием тех или иных видов искажений. При помощи разных проекций можно сделать так чтобы на них отсутствовали погрешности либо углов, либо длин, либо площадей. Чем больше искажаются углы, тем меньше искажаются площади и наоборот. По характеру искажений все картографические проекции делят на:
Равноугольные картографические проекции
На картах, построенных по этому типу, нет искажений направлений и углов. Направления на местности совпадают с таковыми на карте, прямые линии на местности остаются прямыми на карте. Они используются для прокладки точных маршрутов и применяется на навигационных и топографических картах.
Зато на них сильно изменены площади объектов Земли и линейный масштаб карты зависит от положения на ней данной точки. Типичный пример равноугольной проекции – цилиндрическая проекция Герхарда Меркатора (Герарда Кремера), созданная ещё в 1569 г и используемая в морской навигации до сих пор. Примером использования Проекции Меркатора является равноугольная проекция Гаусса-Крюгера.
В этой проекции создаются отдельные океанологические, климатические и геофизические карты.

Файл доступен по лицензии: Creative Commons Attribution-Share Alike 3.0 Unported
Равновеликие картографические проекции
Это проекции для построении карт, на которых нет искажения площадей (масштаб площадей имеет везде одну и ту же величину), зато сильно растёт погрешность форм и углов (материки и океаны в высоких широтах сплющиваются). Картами, построенными в равновеликих проекциях, удобно пользоваться для расчета площадей, например типов почв, посадок кукурузы, облесенности материков, загрязнения океана или радиоактивного загрязнения суши и др.
Их применяют для составления климатических, почвенных, геофизических, геологических, зоогеографических, геоботанических, экономических, исторических, этнографических, административных карт.

Произвольные картографические проекции
Углы и площади здесь искажаются, но значительно меньше, чем в предыдущих двух проекциях. Поэтому они наиболее используемы. Произвольные картографические проекции не относятся ни к равновеликим, ни к равноугольным.

Равнопромежуточные картографические проекции
Это тип произвольных картографических проекций. В них масштаб длин одного из главных направлений остаётся неизменным. Пример: прямая азимутальная проекция. Равнопромежуточные проекции используют для создания общегеографических, физических, тектонических, политических и др. видов карт.
Характер искажения всегда входит в общее название проекции (равновеликая азимутальная, равноугольная коническая, равновеликая цилиндрическая и т.д.).
Интересно,
что д ревнейшей картографической проекцией является гномическая проекция, применённая на картах звёздного неба Фалесом Милетским ещё в Древней Греции.

Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью
На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.
Проекции также бывают по-разному ориентированы.
Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:
Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.
Ликбез по картографическим проекциям с картинками
Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.
Легкое введение
Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.
Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.
Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.
Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.
Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.
Проблема
Начнем с того, что же это за самые распространенные проекции, и что с ними не так.
Первая проекция — так называемая «Географическая», она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).
Другая весьма популярная проекция — «проекция Меркатора», Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).
На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.
Варианты решения
Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами: «Тройная проекция Винкеля» Winkel Tripel WKID:54042 PROJ.4:wintri, «проекция Робинсона» Robinson projection WKID:54030 PROJ.4:robin, «проекция Каврайского» (Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.
Вот так описание этой проекции выглядит в формате ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,0],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]
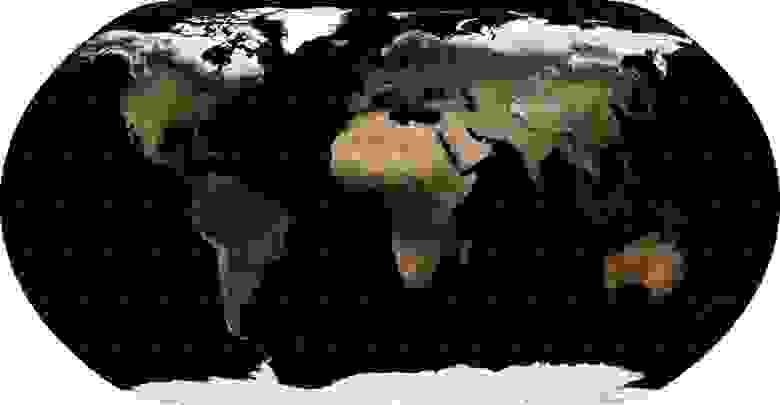
Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.
Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:
А вот измененное для этого случая описание в ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,11],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]
В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.
11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.
Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.
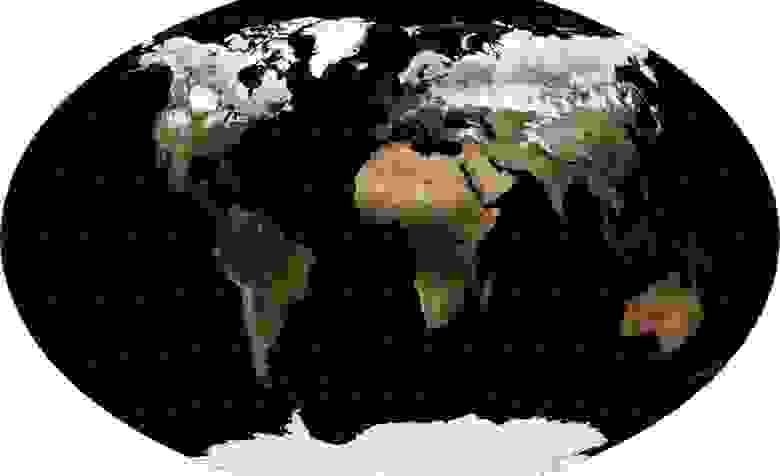
Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции — «проекцию Моллвейде», Mollweide projection WKID:54009 PROJ.4:moll.
Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.
Самым молодым конкурентом этих проекций является проекция Natural Earth PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.
Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.
Немного экзотики и специальных случаев
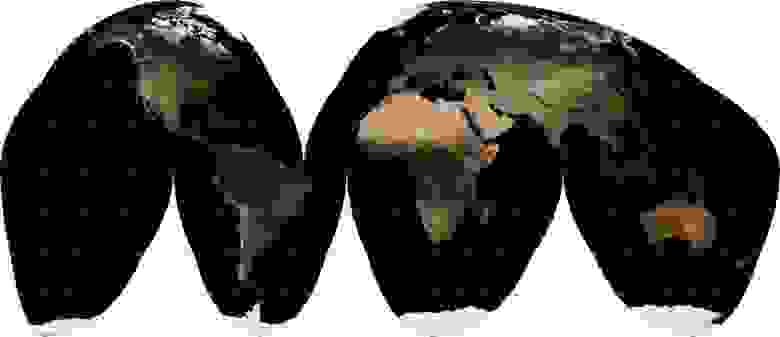
Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была «Разрывная гомолосинусоидальная проекция Гуда» Interrupted Goode Homolosine projection WKID:54052.
Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.
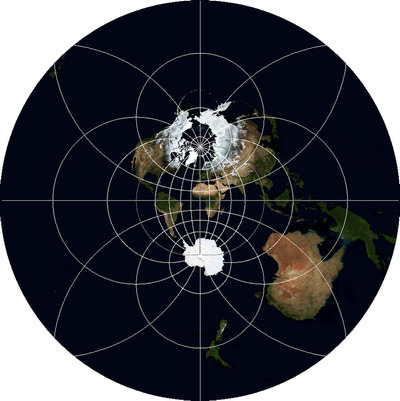
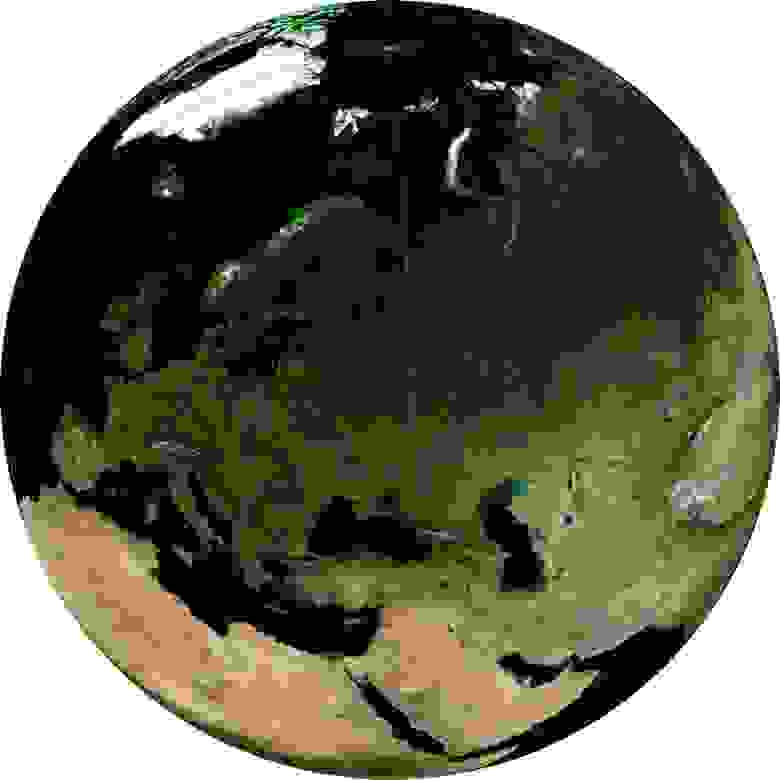
На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется «Ортографическая проекция» Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.
Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.
Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.
Виды картографических проекций
Что такое картографическая проекция?
Картографическая проекция — это способ сгладить трехмерную поверхность земного шара (или другого сферического тела) в плоскость для того, чтобы сделать карту. Это требует систематического преобразования широт и долгот местоположений поверхности сферы в местоположения на плоскости. Этот процесс обычно математический, но некоторые методы основаны на графике.
Все проекции имеют искажения. Они бывают следующих видов: искажения форм, искажения площадей, искажения длин, искажения углов. Особенно большими искажения бывают на мелкомасштабных картах, на крупномасштабных они практически неощутимы.
Цилиндрическая проекция
Цилиндрические картографические проекции являются одним из способов изображения Земли. В этом виде проекции параллели нормальной сетки параллельные прямые, а меридианы перпендикулярные параллелям прямые; расстояния между ними пропорциональны разностям долгот. Единственный фактор, который отличает разные цилиндрические проекции друг от друга, — это масштаб, используемый при разнесении параллельных линий на карте.

Цилиндрические проекции. Равноугольная Меркатора
Недостатки цилиндрических проекций в том, что они сильно искажены на полюсах. Хотя области вблизи экватора с большей вероятностью будут точными в сравнению с реальной Землей, параллели и меридианы, являющиеся прямыми линиями, не учитывают искривление Земли. Цилиндрические отлично подходят для сравнения широт друг с другом и полезны для обучения и визуализации мира в целом, но на самом деле не являются наиболее точным способом визуализации того, как мир действительно выглядит в целом.
Типы цилиндрических картографических проекций, которые вы можете знать, включают в себя популярные проекции Меркатора, Кассини, Гаусса-Крюгера, Миллера, Бермана, Хобо-Дайера и Галла-Петерса.
Коническая проекция карты
Канонические проекции включают эквидистантную коническую проекцию, конформную коническую проекцию Ламберта и конику Альберса. Эти карты имеют конусную константу, которая определяет угловое расстояние между меридианами. Эти меридианы являются равноотстоящими и прямыми линиями, которые сходятся в местах вдоль проекции независимо от того, есть ли полюс или нет. Как и цилиндрическая проекция, проекции конической карты имеют параллели, которые пересекают меридианы под прямым углом с постоянной мерой искажения повсюду.
Проекции конической карты разработаны так, чтобы их можно было обернуть вокруг конуса на вершине сферы (шара), но они не должны быть геометрически точными.

Проекция Альберса является примером проекции конической карты
Конические проекции лучше всего подходят для использования в качестве региональных карт или карт полушария, редко для полной карты мира. Искажение на конической карте делает его неподходящим для использования в качестве визуального изображения всей Земли, но делает его отличным для визуализации умеренных регионов, карт погоды, климатических проекций и многого другого.









Азимутальная картографическая проекция
В азимутальной проекции параллели нормальной сетки являются концентрическими кругами, а меридианы — их радиусами, расходящимися из общего центра параллелей под углами, равными разности долгот. Каждая точка на карте имеет тот же самый азимут по отношению к среднему меридиану, который эта же точка имеет со средним меридианом на сфере.

Азимутальная равновеликая проекция Ламберта 
Эквидистантная азимутальная проекция с северного полюса
Азимутальная картографическая проекция является угловой — учитываются три точки на карте (A, B и C), азимут от точки B до точки C определяет угол, на который кто-то должен смотреть или двигаться, чтобы добраться до A. Эти угловые отношения более известны как дуги большого круга или геодезические дуги. Азимутальные карты полезны для определения направления в любой точке Земли, используя центральную точку в качестве ориентира.
5.3. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ
Для различных целей создаются различные по характеру искажений проекции. Характер искажений проекции определяется отсутствием в ней определенных искажений (углов, длин, площадей). В зависимости от этого все картографические проекции по характеру искажений подразделяются на четыре группы:
— равноугольные (конформные);
— равнопромежуточные (эквидистантные);
—равновеликие (эквивалентные);
— произвольные.
5.3.1. Равноугольные проекции
Равноугольными называются такие проекции, в которых направления и углы изображаются без искажений. Углы, измеренные на картах равноугольных проекций, равны соответствующим углам на земной поверхности. Бесконечно малая окружность в этих проекциях всегда остается окружностью.
В равноугольных проекциях масштабы длин в любой точке по всем направлениям одинаковы, поэтому у них нет искажения формы бесконечно малых фигур и нет искажения углов (рис. 5.7, Б). Это общее свойство равноугольных проекций выражает формула ω = 0°. Но формы реальных (конечных) географических объектов, занимающих целые участки на карте, искажаются (рис. 5.8, а). У равноугольных проекций наблюдаются особенно большие искажения площадей (что отчетливо демонстрируют эллипсы искажений).
Рис. 5.7. Вид эллипсов искажений в проекциях равновеликих —- А, равноугольных — Б, произвольных — В, в том числе, равнопромежуточных по меридиану — Г и равнопромежуточных по параллели — Д. На схемах показано искажение угла 45°.
Эти проекции используются для определения направлений и прокладки маршрутов по заданному азимуту, поэтому их всегда используют на топографических и навигационных картах. Недостатком равноугольных проекций является то, что в них сильно искажаются площади (рис. 5.7, а).

Рис. 5.8. Искажения в цилиндрической проекции:а – равноугольной; б – равнопромежуточной; в – равновеликой









5.6.2. Равнопромежуточные проекции
Равнопромежуточными проекциями называют проекции, у которых масштаб длин одного из главных направлений сохраняется (остается неизменным) (рис. 5.7, Г. рис. 5.7, Д.) Применяются главным образом для создания мелкомасштабных справочных карт и карт звездного неба.
5.6.3. Равновеликие проекции
Равновеликими называются проекции, в которых нет искажений площадей, т. е. площадь фигуры, измеренной на карте, равна площади этой же фигуры на поверхности Земли. В равновеликих картографических проекциях масштаб площади повсюду имеет одну и ту же величину. Это свойство равновеликих проекций можно выразить формулой:
P = a× b = Const = 1 (5.15)
Неизбежным следствием равновеликости этих проекций является сильное искажение у них углов и форм, что хорошо поясняют эллипсы искажений (рис. 5.7, A).
5.6.4. Произвольные проекции
К произвольным относятся проекции, в которых имеются искажения длин, углов и площадей. Необходимость использования произвольных проекций объясняется тем, что при решении некоторых задач возникает необходимость в измерении углов, длин и площадей на одной карте. Но ни одна проекция не может быть одновременно и равноугольной, и равнопромежуточной, и равновеликой. Ранее уже говорилось, что с уменьшением изображаемого участка поверхности Земли на плоскости уменьшаются и искажения изображения. При изображении небольших участков земной поверхности в произвольной проекции величины искажений углов, длин и площадей незначительны, и при решении многих задач их можно не учитывать.
7.10. СПОСОБ КОЛИЧЕСТВЕННОГО ФОНА
Этот способ, как и способ качественного фона, отображает подразделение территории на однородные районы, но по количественному показателю (или показателям). Для этого по имеющимся источникам выделяют согласно разработанной ступенчатой шкале однородные районы, которые затем раскрашивают цветом разной насыщенности или покрывают соответствующими штриховками. При применении количественного фона линии на карте разграничивают выделенные однородные районы, причем смежные районы могут передавать величину явления, соответствующую противоположным ступеням шкалы.
Для использования этого способа требуется хорошая изученность территории по определенным показателям в количественном отношении. Очень часто для построения карт необходимо выполнение картографических работ, например составление морфометрических карт по топокартам (густоты и глубины расчленения рельефа, крутизны склонов и др.).
Способ количественного фона используется главным образом для составления карт природы (геоморфологических, гидрологических, гидрогеологических и др.), но его можно встретить и на социально-экономических картах, например на картах плотности населения.

Рис. 7.10. Количественный фон.
Возможно сочетание качественного и количественного фонов, например при выделении районов преобладающих конфессий (качественный фон) с дополнительной характеристикой процентного соотношения населения разного вероисповедания (количественный фон).
Вопросы и задания для самоконтроля
ArcGIS автоматически интегрирует данные в известных системах координат
Все географические данные, используемые в ArcGIS, предполагают наличие корректной системы координат, что позволяет им быть локализованными на реальной земной поверхности.
Если данные имеют корректную систему координат, ArcGIS может автоматически интегрировать их «на лету» с другими спроецированными данными в соответствующую среду – для картографирования, трехмерной визуализации, анализа и т.д.









Если данные не имеют пространственной привязки, их невозможно интегрировать. Необходимо определить ее до того, как вы начнете использовать эти данные в ArcGIS. Пространственная привязка (система координат) является метаданными. Она описывает систему координат, которую используют данные.
Методы получения проекций
Изучая картографические проекции, их виды и свойства необходимо упомянуть о методах их построения. Итак, картографические проекции получают, используя два основных метода:
В основе геометрического метода лежат закономерности линейной перспективы. Наша планета условно принимается сферой некоторого радиуса и проецируется на цилиндрическую или коническую поверхность, которая может либо касаться, либо рассекать ее.
Проекции, полученные подобным способом, называются перспективными. В зависимости от положения точки наблюдения относительно поверхности Земли перспективные проекции разделяют на виды:
Аналитический метод построения картографических проекций базируется на математических выражениях, связывающих точки на сфере относимости и плоскости отображения. Такой метод является более универсальным и гибким, позволяя создавать произвольные проекции по заранее заданному характеру искажения.
7.1. КАРТОГРАФИЧЕСКАЯ СЕМИОТИКА
Язык карты – это используемая в картографии знаковая система, включающая условные обозначения, способы изображения, правила их построения, употребления и чтения при создании и использовании карт. Во все времена язык карты не только обеспечивал хранение и передачу пространственно-временной информации, но и играл роль общего языка в науках о Земле и смежных с ними отраслях знания.
На стыке картографии и семиотики – лингвистической науки, исследующей свойства знаков и знаковых систем, сформировался особый раздел картографическая семиотика, в рамках которой разрабатывается общая теория систем картографических знаков как языка карты.
В ней изучается довольно обширный круг проблем, касающихся происхождения, классификации, свойств и функций картографических знаков и способов картографического изображения. Семиотика включает три основных раздела: синтактику, семантику и прагматику, соответственно эти разделы существуют и в картографической семиотике:
картографическая синтактика – изучает правила построения и употребления знаковых систем, их структурные свойства, грамматику языка карты;
картографическая семантика – исследует соотношения условных знаков с самими отображаемыми объектами и явлениями;
картографическая прагматика – изучает информационную ценность знаков как средства коммуникации и особенности их восприятия читателями карты. Иногда в составе картографической семиотики выделяют еще один раздел – картографическую стилистику, изучающую стили и факторы, которые определяют выбор изобразительных средств в соответствии с назначением и функциями картографических произведений.
Исследования показали, что в языке карты можно различить, по крайней мере, два слоя (подъязыка): один из них отражает размещение картографируемых объектов, их пространственную форму, ориентацию, взаимное положение, другой – содержательную сущность этих явлений, их внутреннюю структуру, качественные и количественные характеристики. Грамматика обоих подъязыков определяется правилами картографической семиотики.
Язык карты – это объектный язык картографии. Его главные функции (как и картографии вообще) – коммуникативная, т.е. передача некоторого объема информации от создателя карты к читателю, и познавательная – получение новых знаний о картографируемом объекте.
5.6. ВЫБОР ПРОЕКЦИЙ
На выбор проекций влияет много факторов, которые можно сгруппировать следующим образом:
Первые три группы факторов задаются изначально, четвертая – зависит от них. Если составляется карта, предназначенная для навигации, обязательно должна быть использована равноугольная цилиндрическая проекция Меркатора. Если картографируется Антарктида, то почти наверняка будет принята нормальная (полярная) азимутальная проекция и т.д.
Значимость названных факторов может быть различной: в одном случае на первое место ставят наглядность (например, для настенной школьной карты), в другом – особенности использования карты (навигация), в третьем – положение территории на земном шаре (полярная область). Возможны любые комбинации, а следовательно – и разные варианты проекций. Тем более что выбор очень велик. Но все же можно указать некоторые предпочтительные и наиболее традиционные проекции.Карты мира обычно составляют в цилиндрических, псевдоцилиндрических и поликонических проекциях. Для уменьшения искажений часто используют секущие цилиндры, а псевдоцилиндрические проекции иногда дают с разрывами на океанах.Карты полушарий всегда строят в азимутальных проекциях. Для западного и восточного полушарий естественно брать поперечные (экваториальные), для северного и южного полушарий – нормальные (полярные), а в других случаях (например, для материкового и океанического полушарий) — косые азимутальные проекции.Карты материков Европы, Азии, Северной Америки, Южной Америки, Австралии с Океанией чаще всего строят в равновеликих косых азимутальных проекциях, для Африки берут поперечные, а для Антарктиды – нормальные азимутальные.Карты отдельных стран, административных областей, провинций, штатов выполняют в косых равноугольных и равновеликих конических или азимутальных проекциях, но многое зависит от конфигурации территории и ее положения на земном шаре. Для небольших по площади районов задача выбора проекции теряет актуальность, можно использовать разные равноугольные проекции, имея в виду, что искажения площадей на малых территориях почти неощутимы.Топографические карты Украины создают в поперечно-цилиндрической проекции Гаусса, а США и многие другие западные страны – в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно UТМ). Обе проекции близки по своим свойствам; по существу та и другая являются многополостными.Морские и аэронавигационные карты всегда даются исключительно в цилиндрической проекции Меркатора, а тематические карты морей и океанов создают в самых разнообразных, иногда довольно сложных проекциях. Например, для совместного показа Атлантического и Северного Ледовитого океанов применяют особые проекции с овальными изоколами, а для изображения всего Мирового океана – равновеликие проекции с разрывами на материках.
В любом случае при выборе проекции, в особенности для тематических карт, следует иметь в виду, что обычно искажения на карте минимальны в центре и быстро возрастают к краям









Кроме того, чем мельче масштаб карты и обширнее пространственный охват, тем большее внимание приходится уделять «математическим» факторам выбора проекции, и наоборот – для малых территорий и крупных масштабов более существенными становятся «географические» факторы
7.8. СПОСОБ АРЕАЛОВ.
Способ ареалов (от латинского слова area — площадь, участок) заключается в том, что площадь, на которой распространено картографируемое явление, особым обозначением выделяется из всей изображенной на карте территории. Применяется главным образом для качественной характеристики картографируемой территории,
Этим способом на тематических картах показывают области распространения культурных и диких видов растений или животных, бессточные области, районы плавучих льдов в море, районы залегания полезных ископаемых, на исторических картах могут быть показаны территории, охваченные крестьянскими восстаниями, и многие другие явления.
Ареалы бывают абсолютные, вне которых данное явление не встречается, и относительные, внутри которых данное явление обладает определенными свойствами (например, ареал промышленной разработки каменного угля в пределах области его залегания). Относительный ареал более узок – он показывает места наибольшего сосредоточения явления. Ареалы подразделяются на точные и схематичные в зависимости от использования действительных (достоверных) или мнимых границ. Если объект картографирования имеет точные границы, то и ареал будет точным. Для схематических ареалов характерно приближенное отображение явления, когда нет точных данных о его размещении или для данного явления свойственна неопределенность границ в природе.
Ареалы распространения разных видов растений, животных и т. п. могут иметь различные пространственные соотношения: они могут находиться на некотором расстоянии один от другого, могут соприкасаться друг с другом или взаимно перекрываться. Графически возможности изображения ареалов разнообразны: это сплошная или пунктирная линия различного рисунка и цвета, окраска или цветные штриховки, геометрические или наглядные значки или даже надпись (рис. 7.7).

Рис. 7.7. Графические способы показа ареала на карте
Границы как графическое средство, преимущественно применяются для абсолютных ареалов, для относительных – значки или надписи. Причем, отличие значка ареала от значка значкового способа заключаются в том, что в первом случае он характеризует площадь, а во втором – показывает объект точно, локализовано. Границы показывают не линейный объект, а только оконтуривают ареал.
На карте «Австралия, Новая Зеландия. Месторождения полезных ископаемых» (рис. 7.8), показаны важные месторождения полезных ископаемых. Металлические руды показаны химическими символами периодической системы Д.И.Менделеева, неметаллические и полиметаллические руды – геометрическими знаками разного рисунка.

Рис. 7.8. Австралия, Новая Зеландия. Месторождения полезных ископаемых
5.7. РАСПОЗНАВАНИЕ ПРОЕКЦИЙ
Распознать проекцию, в которой составлена карта, – значит установить ее название, определить принадлежность к тому или иному виду, классу. Это нужно для того, чтобы иметь представление о свойствах проекции, характере, распределении и величине искажений – словом, для того, чтобы знать, как пользоваться картой, чего от нее можно ожидать.
Некоторые нормальные проекции сразу распознаются по виду меридианов и параллелей. Например, легко узнаваемы нормальные цилиндрические, псевдоцилиндрические, конические, азимутальные проекции. Но даже опытный картограф не сразу распознает многие произвольные проекции, потребуются специальные измерения по карте, чтобы выявить их равноугольность, равновеликость или равнопромежуточность по одному из направлений. Для этого существуют особые приемы: сперва устанавливают форму рамки (прямоугольник, окружность, эллипс), определяют, как изображены полюсы, затем измеряют расстояния между соседними параллелями вдоль по меридиану, площади соседних клеток сетки, углы пересечения меридианов и параллелей, характер их кривизны и т.п.
Существуют специальные таблицы-определители проекций для карт мира, полушарий, материков и океанов. Проведя необходимые измерения по сетке, можно отыскать в такой таблице название проекции. Это даст представление о ее свойствах, позволит оценить возможности количественных определений по данной карте, выбрать соответствующую карту с изоколами для внесения поправок.
ВидеоВиды проекций по характеру искажений
Вопросы для самоконтроля: