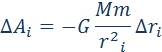Как кеплер открыл свои законы
Как кеплер открыл свои законы
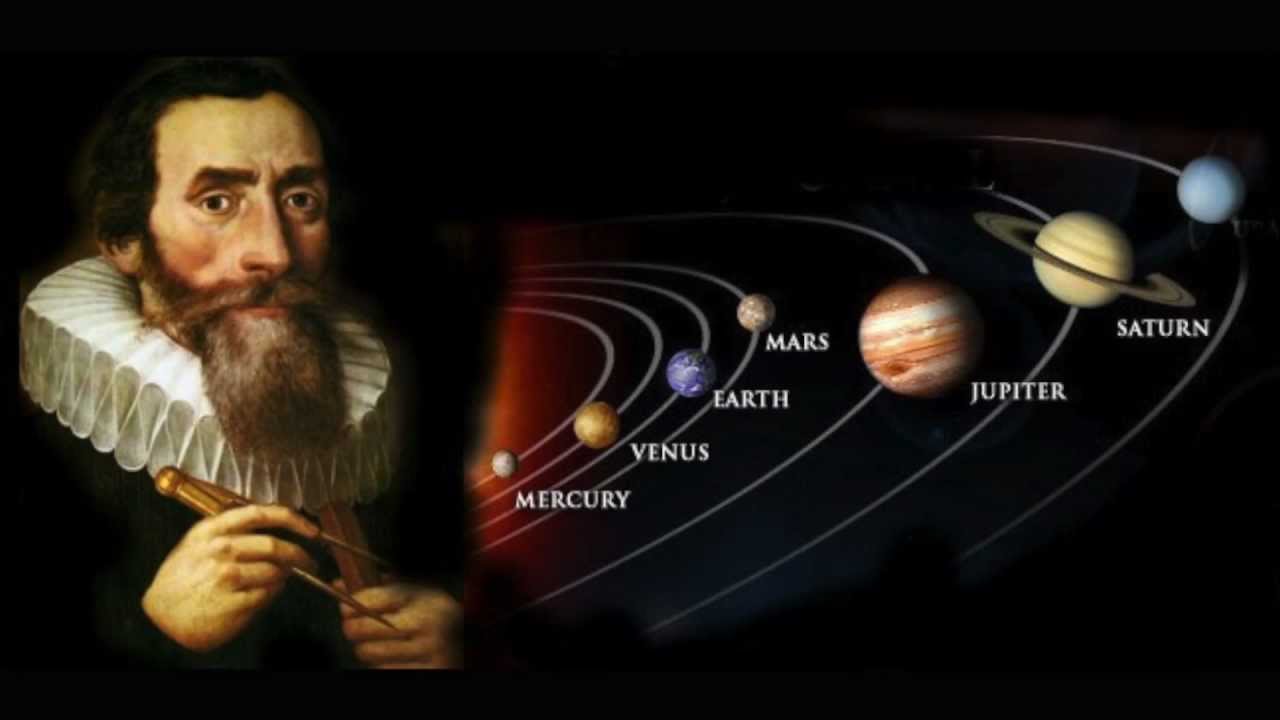
Johannes Kepler, 1571–1630
Немецкий астроном. Родился в Вюртембурге. Начав с изучения богословия в Тюбингенской академии (позднее университет), увлекся математикой и астрономией и вскоре получил приглашение на должность преподавателя математики в гимназии австрийского города Грац. Там он снискал себе репутацию блестящего астролога благодаря ряду сбывшихся метеорологических прогнозов на 1595 год. Начиная с 1598 года Кеплер и другие протестанты стали подвергаться в католическом Граце жестоким религиозным гонениям, и в 1600 году ученый по приглашению датского астронома Тихо Браге переехал в Прагу. Работы Кеплера основывались на наблюдениях, сделанных Тихо Браге. Его дальнейшая жизнь сложилась трагично. Он жил в бедности и умер от лихорадки по дороге в Австрию, куда он отправился в надежде получить причитающееся ему жалованье.
Ч ем ближе планеты к Солнцу, тем больше линейная и угловая скорости их обращения вокруг Солнца. Период обращения планет вокруг Солнца по отношению к звездам называется звездным периодом.
Такой период обращения Земли относительно звезд называется звездным годом. Наименьший звездный период обращения у планеты Меркурий. У Марса он составляет около 2 лет, у Юпитера — 12 лет и, все возрастая с удалением от Солнца, у Плутона доходит до 250 лет.
Заслуга открытия законов движения планет принадлежит выдающемуся австрийскому ученому Кеплеру. В начале XVII в. Кеплер установил три закона движения планет. Они названы законами Кеплера.
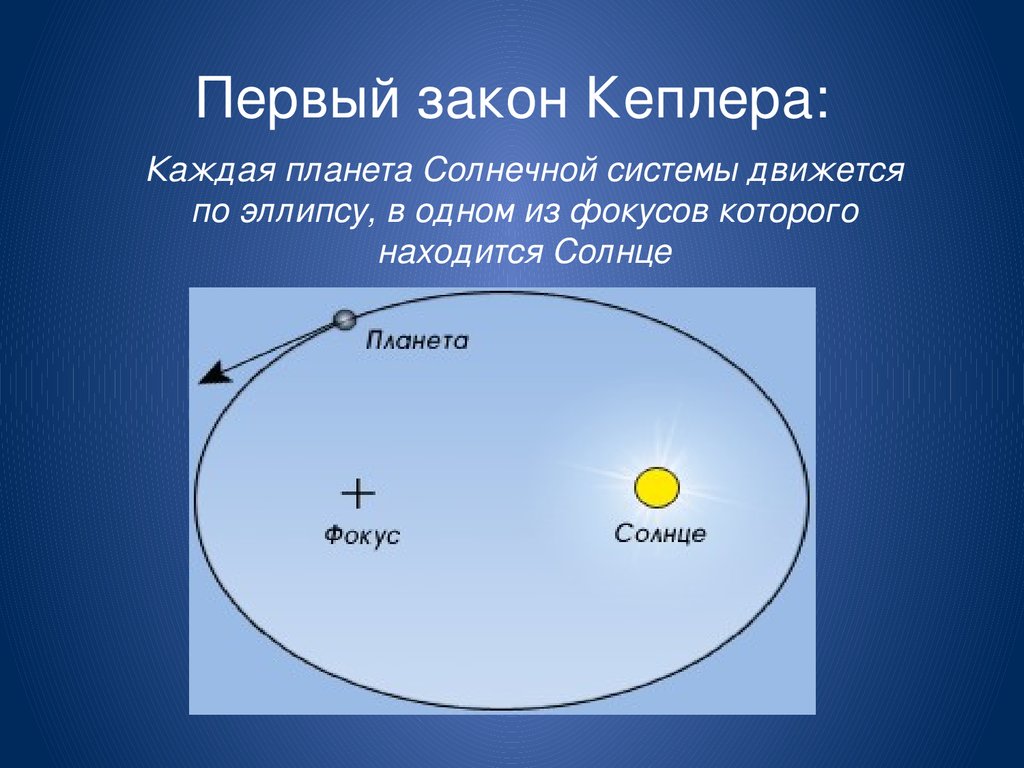
Первый закон Кеплера: каждая планета обращается вокруг Солнца по эллипсу, в одном аз фокусов которого находится Солнце.
Степень вытянутости эллипса характеризуется величиной его эксцентриситета. Эксцентриситет равен отношению расстояния фокуса от центра к длине большой полуоси. В пределе при совпадении фокусов и центра эксцентриситет равен нулю и эллипс превращается в окружность.
Ближайшая к Солнцу точка орбиты называется перигелием, а самая далекая от него точка называется афелием. Орбиты планет — эллипсы, мало отличающиеся от окружностей, их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е = 0,017.
Эксцентриситеты орбит у комет приближаются к единице. При е=1 второй фокус эллипса удаляется (в пределе) в бесконечность, так что эллипс становится разомкнутой кривой, называемой параболой. Ее ветви в бесконечности стремятся стать параллельными. При е>1 орбита является гиперболой. Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.
Кеплер открыл свои законы, изучая периодическое обращение планет вокруг Солнца. Ньютон, исходя из законов Кеплера, открыл закон всемирного тяготения. При этом он нашел, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу, в частности по кругу, по параболе и по гиперболе. Выяснилось, что некоторые кометы огибают Солнце, двигаясь по параболе или по гиперболе. В таком случае они уходят из солнечной системы и уже не являются ее членами.
Средняя скорость движения Земли по орбите 30 км/с. Орбита Земли близка к окружности, а скорость Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость для Земли будет равна √2*30 км/с = 42 км/с. При такой скорости относительно Солнца тело покинет солнечную систему.
Третий закон Кеплера: квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит.
Законы движения Кеплера
Иоганн Кеплер и планеты Солнечной системы
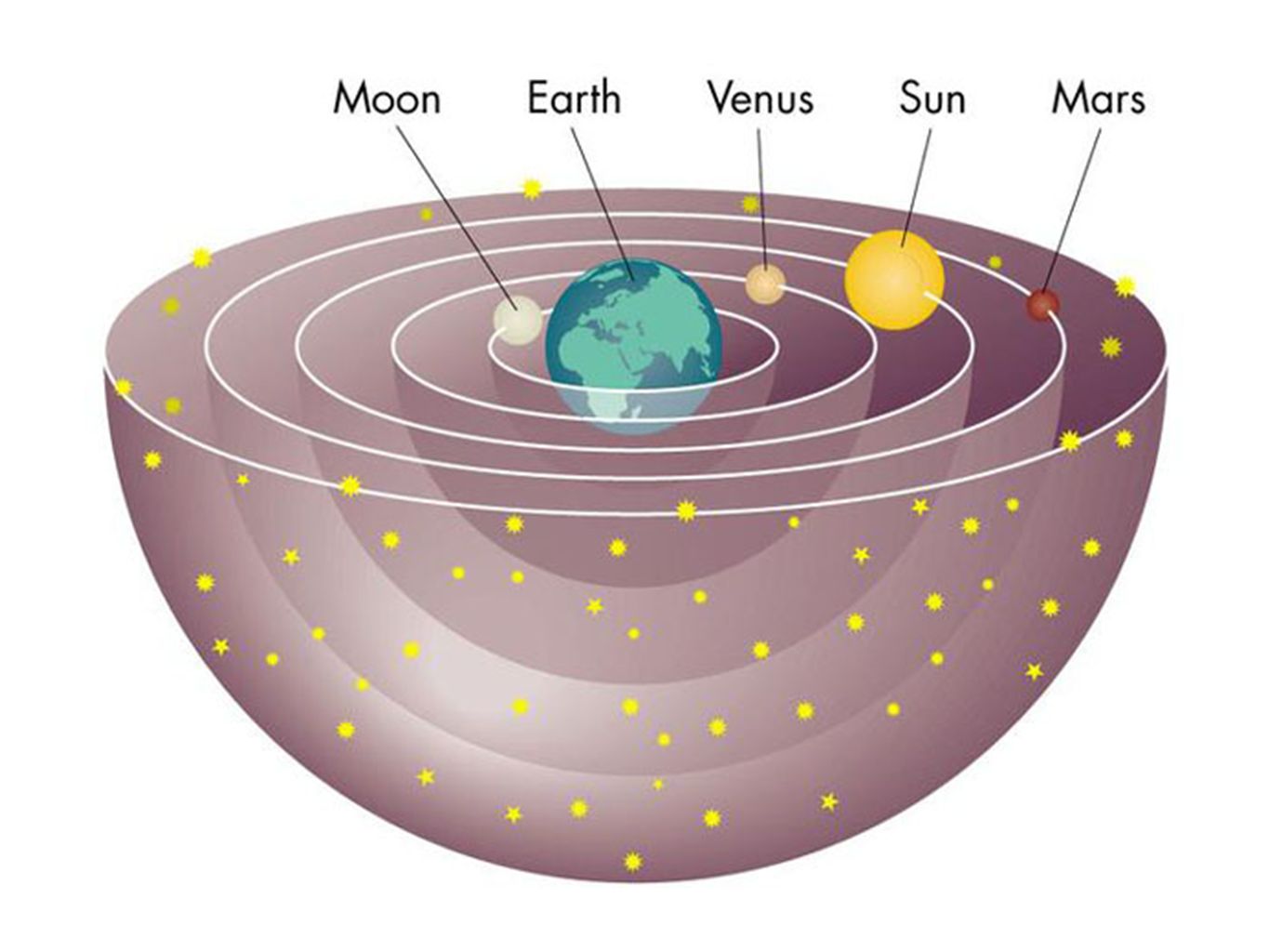
Астрономия конца XVI века отмечает столкновение двух моделей нашей Солнечной системы: геоцентрическая система Птолемея – где центром вращения всех объектов является Земля, и гелиоцентрическая система Коперника – где Солнце является центральным телом.
Модель Солнечной системы Клавдия Птолемея
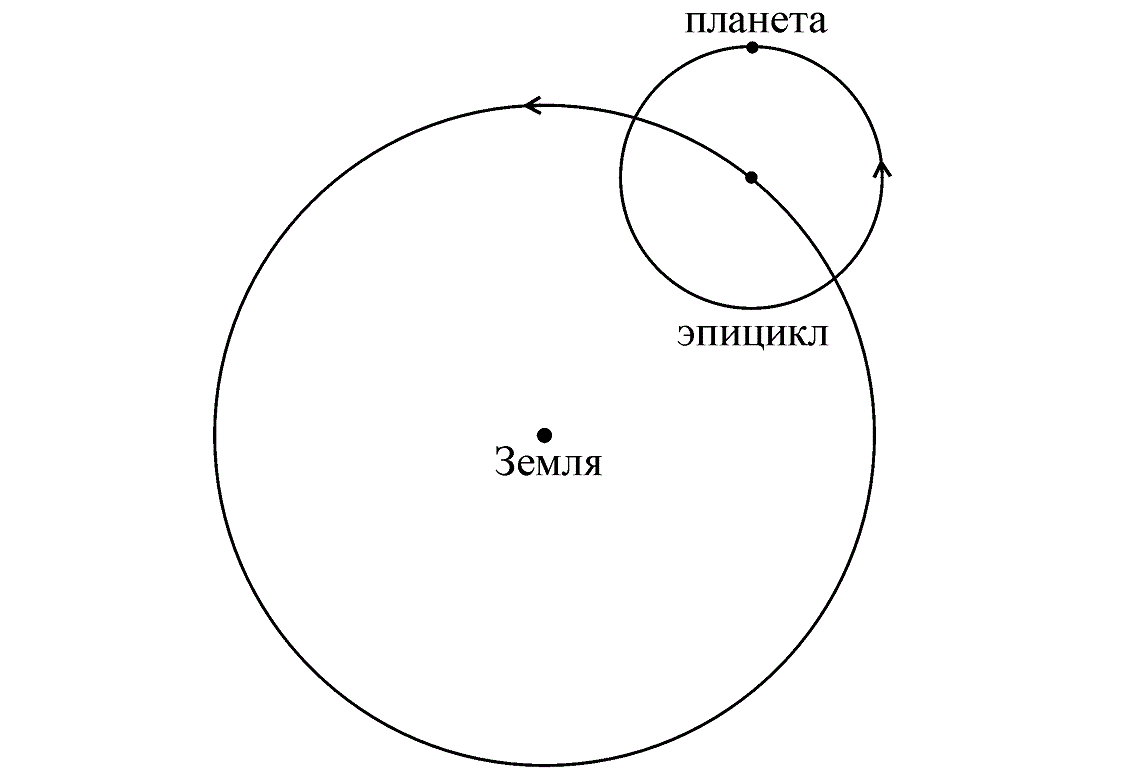
И хотя Коперник был ближе к истинной природе Солнечной системы, его работа имела недостатки. Основным из этих недостатков являлось утверждение, что планеты вращаются вокруг Солнца по круговым орбитам. С учетом этого, модель Коперника практически настолько же не согласовывалась с наблюдениями, как и система Птолемея. Польский астроном стремился исправить данное расхождение при помощи дополнительного движения планеты по кругу, центр которого уже двигался вокруг Солнца — эпицикл. Однако, расхождения в большей своей части не были устранены.
В начале XVII века немецкий астроном Иоганн Кеплер, изучая систему Николая Коперника, а также анализируя результаты астрономических наблюдений датчанина Тихо Браге, вывел основные законы относительно движения планет. Они были названы как Три закона Кеплера.
Первый закон Кеплера
Немецкий астроном пытался различными способами сохранить круговую орбиту движения планет, однако это не позволяло исправить расхождение с результатами наблюдений. Потому Кеплер прибегнул к эллиптическим орбитам. У каждой такой орбиты есть два так называемых фокуса. Фокусы – это две заданные точки, такие, что сумма расстояний от этих двух точек до любой точки эллипса является постоянной.
Иоганн Кеплер отметил, что планета движется по эллиптической орбите вокруг Солнца таким образом, что Солнце располагается в одном из двух фокусов эллипса, что и стало первым законом движения планет.
Первый закон Кеплера
Второй закон Кеплера
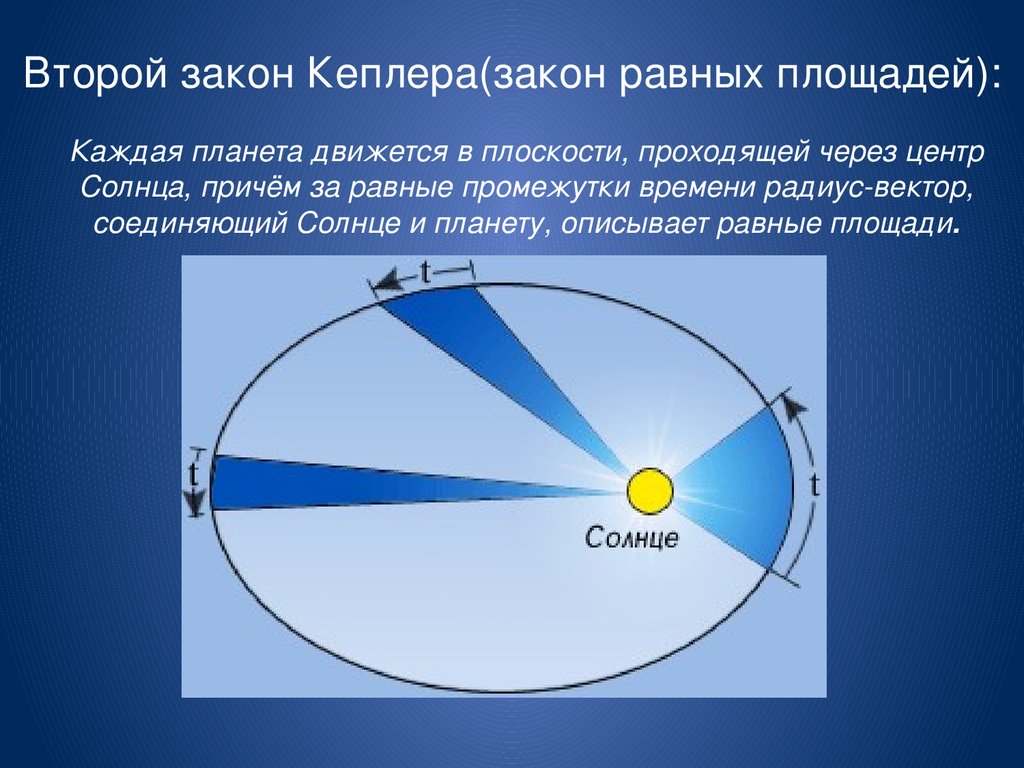
Проведем радиус-вектор от Солнца, которое располагается в одном из фокусов эллипсоидной орбиты планеты, к самой планете. Тогда за равные промежутки времени данный радиус-вектор описывает равные площади на плоскости, в которой движется планета вокруг Солнца. Данное утверждение является вторым законом.
Второй закон Кеплера
Третий закон Кеплера
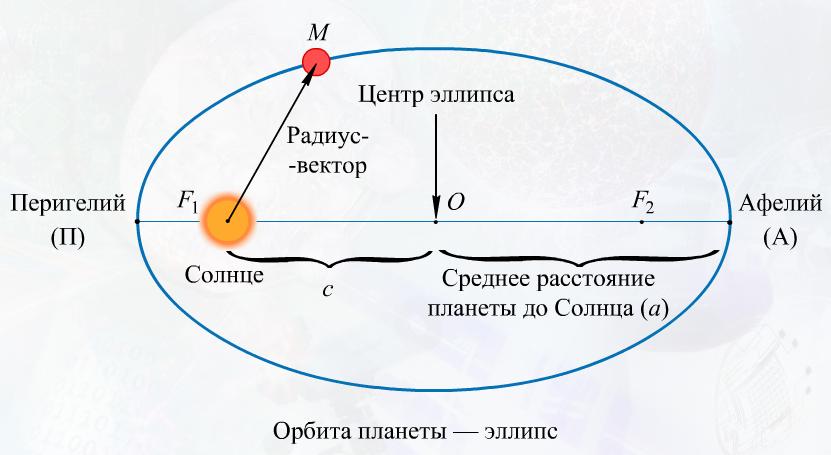
Каждая орбита планеты имеет точку, ближайшую к Солнцу, которое называется перигелием. Точка орбиты, наиболее удаленная от Солнца, называется афелием. Отрезок, соединяющий эти две точки называется большой осью орбиты. Если разделить этот отрезок пополам, то получим большую полуось, которую чаще используют в астрономии.
Основные элементы эллипса
Третий закон движения планет Кеплера звучит следующим образом:
Отношение квадрата периода обращения планеты вокруг Солнца к большой полуоси орбиты этой планеты является постоянным, и также равняется отношению квадрата периода обращения другой планеты вокруг Солнца к большой полуоси этой планеты.
Также иногда записывают другое отношение:
Одна из записей третьего закона
Дальнейшее развитие
И хотя законы Кеплера имели относительно невысокую погрешность (не более 1%), все же они были получены эмпирическим способом. Теоретическое же обоснование отсутствовало. Данная проблема позже была решена Исааком Ньютоном, который в 1682-м году открыл закон всемирного тяготения. Благодаря этому закону удалось описать подобное поведение планет. Законы Кеплера стали важнейшим этапом в понимании и описании движения планет.
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Законы Кеплера
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (
140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
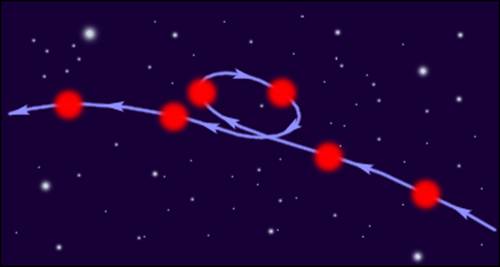 |
| Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд |
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном Иоганн Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Тихо Браге.
Первый закон Кеплера (1609 г.):
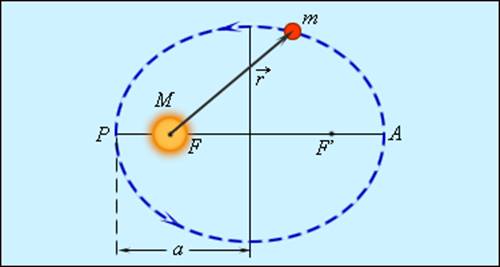
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
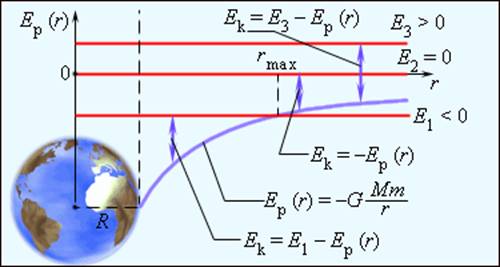
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.




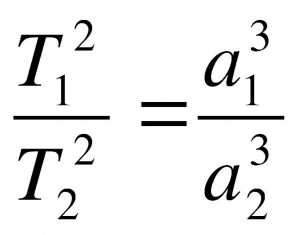
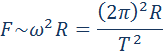
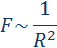
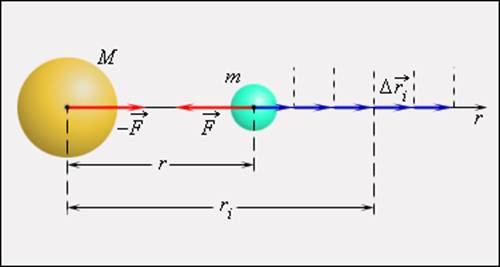
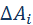 гравитационной силы
гравитационной силы 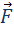 на малом перемещении
на малом перемещении 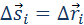 есть:
есть: