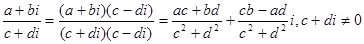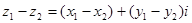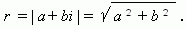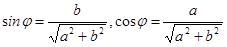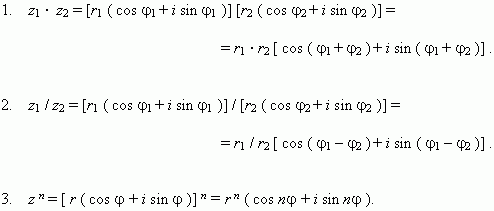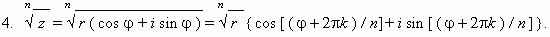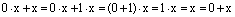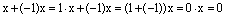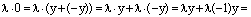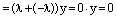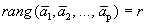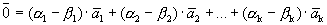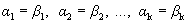Как комплексное число представляют геометрически
Числа. Геометрическое представление комплексных чисел.
Комплексным числом z является пара действительных чисел x и y, упорядоченная.
Первое число x из этой пары является действительной частью комплексного числа z и обозначают его как Rez, x = Rez. Второе число y является мнимой частью комплексного числа z и обозначают его как Imz, y = Imz.
Действительные числа изображают точками на числовой прямой:
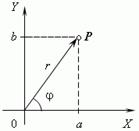
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого, комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b. Эта система координат называется комплексной плоскостью.
Модуль комплексного числа a + bi обозначают |a+ bi| либо буквой r и он равняется:
У сопряженных комплексных чисел равные модули.
Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi выражают через модуль этого числа r и аргумент φ:
Операции с комплексными числами, которые представлены в тригонометрической форме.
Это знаменитая формула Муавра.
Чтобы получить n разных значений корня n-ой степени из z нужно задать n последовательных значений для k (к примеру, k = 0, 1, 2,…, n – 1).
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №39. Геометрическая интерпретация комплексного числа.
Перечень вопросов, рассматриваемых в теме
3) определение модуля комплексного числа.
а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке
Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Геометрическое изображение комплексных чисел.
а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).
Модуль комплексного числа
Как отмечалось выше, комплексное число также можно изображать радиус-вектором 
Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.
Иногда еще модуль комплексного числа обозначается как r или ρ.
Разбор решения заданий тренировочного модуля
№1. Тип задания: единичный выбор
Найдите модуль комплексного числа z=5-3i
Решим данное задание, используя определение модуля.
Верный ответ: 2.
№2. Тип задания: рисование.
Изобразите вектором на комплексной плоскости точку z=2+3i
Разобьем z=2+3i на две части: z1=2 и z2= 3i. Отметим на плоскости точки О и А, соединим их:
Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа
Комплексным числом zназ. выражение 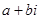
При этом выполняются соглашения:
1) с выражением a+bi можно производить арифметические операции по правилам, которые приняты для буквенных выражений в алгебре;
5) равенство a+bi=c+di, где a, b, c, d – действительные числа, имеет место тогда и только тогда, когда a=c и b=d.
Число 0+bi=bi называется мнимым или чисто мнимым.
Любое действительное число а есть частный случай комплексного числа, ведь его можно записать в виде a=a+ 0i. В частности, 0=0+0i, но тогда ели a+bi=0, то a+bi=0+0i, следовательно, a=b=0.
Т.о., комплексное число a+bi=0 тогда и только тогда, когда a=0 и b=0.
Из соглашений следуют законы преобразования комплексных чисел:
Мы видим, что сумма, разность, произведение и частное (где делитель не равен нулю) комплексных чисел, в свою очередь комплексное число.
Число а наз. вещественной частью комплексного числа z (обозначается 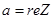
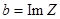
Комплексное число z с нулевой вещественной частью наз. чисто мнимым, с нулевой мнимой – чисто вещественным.
Два комплексных числа наз.равными,если у них совпадают и вещественная и мнимая части.
Два комплексных числа наз. сопряженными, если у них веществ. части совпадают, а мнимые отличаются знаками. 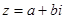
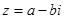
Сумма сопряженных чисел есть число веществ, а разность чисто мнимое число. На множестве комплексных чисел естественным образом определены операции умножения и сложения чисел. Именно, если 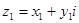
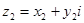
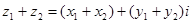
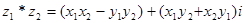
Определим теперь операции вычитания и деления.
Заметим, что произведение двух комплексных чисел есть число веществ.
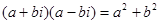
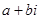
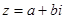
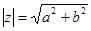
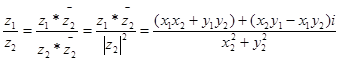
В отличие от вещественных чисел для комплексных чисел не вводится понятие «больше», «меньше».
Геометрическое представление комплексных чисел.Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (рис.). Эта система координат называется комплексной плоскостью.
Модулемкомплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __
Тригонометрическая формакомплексного числа. Наряду с записью комплексного числа в алгебраической форме также употребляется и другая, называемая тригонометрической.
Пусть комплексное число z=a+bi изображается вектором ОА с координатами (a,b). Обозначим длину вектора ОА буковой r: r=|ОА|, а угол, который он образует с положительным направлением оси Ох – через угол φ.
Воспользовавшись определениями функций sinφ=b/r, cosφ=a/r, комплексное число z=a+bi можно записать в виде z=r(cosφ+i*sinφ), где 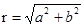
Тригонометрической формой комплексного числа z называется его представление в виде z=r(cosφ+i*sinφ), где r и φ – действительные числа и r≥0.
Действительно число r называется модулем комплексного числа и обозначается |z|, а угол φ – аргументом комплексного числа z. Аргумент φ комплексного числа z обозначается Arg z.
Операции с комплексными числами, представленными в тригонометрической форме:
Это знаменитая формула Муавра.
8.Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов
Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям:
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x+0=x: для любого вектора x;
4) для любого вектора х существует противоположный ему вектор у такой, что х+у =0,
6) α(βx)=(αβ)х (ассоциативность умножения), где произведение αβ есть произведение скаляров
7) (α+β)х=αх+βх (распределительное свойство относительно числового множителя);
8) α(х+у)=αх+αу(распределительное свойство относительно векторного множителя).
Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям 1-8.
Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Теорема “Простейшие свойства векторных пространств”
1. В векторном пространстве существует единственный нулевой вектор.
2. В векторном пространстве любой вектор имеет единственный противоположный ему.
3. 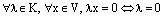
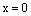
4. 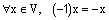
Док-во
Пусть 0 – нулевой вектор векторного пространства V. Тогда 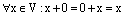
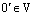
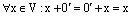
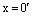
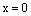
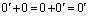
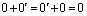
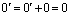
Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.
Пусть 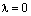
Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует 0*х=0
Теперь докажем утверждение 4). Пусть 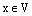
Отсюда сразу же следует, что вектор (-1)х является противоположным вектору х.
Пусть теперь х=0. Тогда, применяя аксиомы векторного пространства, 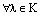

Пусть 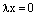
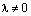
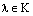
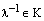
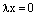
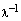
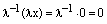
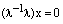
Линейная зависимость и независимость системы векторов. Набор векторов 
Система из 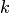

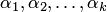
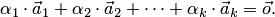
Система из k векторов 
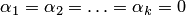
Замечания:
1. Один вектор 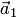
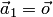
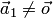
2. Любая часть системы векторов называется подсистемой.
Свойства линейно зависимых и линейно независимых векторов:
1. Если в систему векторов входит нулевой вектор, то она линейно-зависима.
2. Если в системе векторов имеется два равных вектора, то она линейно-зависима.
3. Если в системе векторов имеется два пропорциональных вектора 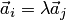
4. Система из k>1 векторов линейно-зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно-независимую систему, образуют линейно-независимую подсистему.
6. Система векторов, содержащая линейно-зависимую подсистему, линейно-зависима.
7. Если система векторов 
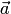
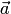

Тогда из равенства 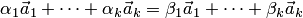
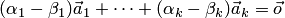
Следовательно, линейная комбинация векторов 
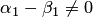

Ранг и базис системы векторов. Рангом системы векторов называется максимальное число линейно-независимых векторов системы.
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
Док-во:
Пусть система 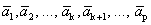
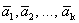
1 случай. Вектор 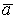
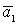
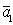
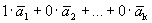
2 случай. Вектор 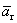
Рассмотрим систему векторов 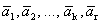
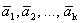
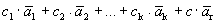
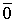
Очевидно, что 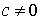
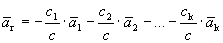
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
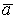
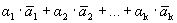
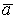
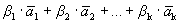
Вычитая эти равенства, получим
Учитывая линейную независимость векторов базиса, получим
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.