Как компьютер выбирает случайное число
Как компьютеры выбирают случайные числа – псевдослучайные числа
Компьютеры могут генерировать поистине случайные числа, наблюдая за некоторыми внешними данными, такими как движения мыши или шум вентилятора, который не предсказуем и создают данные из него. Это называется энтропией. В других случаях они генерируют «псевдослучайные» числа, используя алгоритм, поэтому результаты кажутся случайными, хотя таковыми не являются.
Эта тема становится всё более спорной в последнее время, и вызывает сомнение у большого количества людей. Чтобы понять, почему это может быть ненадежным, вам нужно понять, как используются случайные числа и для чего они нужны.
Как используют случайные числа
Случайные числа использовались в течение многих тысяч лет. Независимо от того, подкидывали ли монету или бросали кости, цель заключалась в том, чтобы получить случайный результат. Генераторы случайных чисел на компьютерах похожи – они пытаются достичь непредсказуемого случайного результата.
Генераторы случайных чисел полезны для разных целей. Помимо очевидных приложений, таких как генерация случайных чисел для азартных игр или создания непредсказуемых результатов в компьютерной игре, случайность важна для криптографии.
Криптография требует использования чисел, о которых не смогут догадаться третьи лица. Мы не можем просто использовать одни и те же числа снова и снова. Мы хотим генерировать эти цифры очень непредсказуемым образом, чтобы злоумышленники не могли их угадать. Эти случайные числа необходимы для безопасного шифрования, независимо от того, шифруете ли вы свои собственные файлы или подключаетесь к веб-сайту по HTTPS.
Истинные случайные числа
Возможно, вам интересно, как компьютер может генерировать случайное число. Откуда возникает эта «случайность». Если это всего лишь фрагмент компьютерного кода, возможно ли, что числа, которые генерирует компьютер, могут быть непредсказуемыми?
Обычно мы группируем случайные числа, создаваемые компьютером, в два типа, в зависимости от того, как они генерируются: «истинные» случайные числа и псевдослучайные числа.
Для генерации «истинного» случайного числа компьютер измеряет некоторый тип физического явления, которое происходит за пределами компьютера. Например, компьютер может измерять радиоактивный распад атома. Согласно квантовой теории, нет никакого способа точно знать, когда произойдет радиоактивный распад, так что это «чистая случайность». Злоумышленник не сможет предсказать, когда произойдет радиоактивный распад, поэтому они не будут знать случайное значение.
В бытовом случае компьютер может опираться на атмосферный шум или просто использовать точное время нажатия клавиш на клавиатуре в качестве источника непредсказуемых данных или энтропии. Например, ваш компьютер может заметить, что вы нажали клавишу ровно в 0,23423523 секунды после 2 часов дня. Это достаточный источник энтропии, который можно использовать для создания «истинного» случайного числа. Вы не предсказуемая машина, поэтому злоумышленник не сможет угадать точный момент, когда вы нажимаете эти клавиши.
Псевдослучайные числа
Псевдослучайные числа являются альтернативой «истинным» случайным числам. Компьютер может использовать начальное значение и алгоритм для генерации чисел, которые кажутся случайными, но которые, на самом деле, предсказуемы. Компьютер не собирает никаких случайных данных из среды.
Это не обязательно плохо. Например, если вы играете в видеоигру, не имеет значения, связаны ли события, происходящие в этой игре, с «истинными» случайными числами или псевдослучайными числами. С другой стороны, если вы используете шифрование, вряд ли Вам захочется использовать псевдослучайные числа, которые может угадать злоумышленник.
Например, злоумышленник знает алгоритм и начальное значение, которое использует генератор псевдослучайных чисел. Предположим, что алгоритм шифрования получает псевдослучайное число из этого алгоритма и использует его для генерации ключа шифрования без добавления дополнительной случайности. Если злоумышленник знает достаточно, он сможет «повернуть процесс вспять» и определять псевдослучайное число, вмешавшись в шифрование.
NSA и аппаратный генератор случайных чисел Intel
Чтобы упростить работу разработчиков и помочь генерировать безопасные случайные числа, чипы Intel включают аппаратный генератор случайных чисел, известный как RdRand. Этот чип использует источник энтропии на процессоре и предоставляет случайные числа для программного обеспечения, когда программное обеспечение запрашивает их.
Проблема здесь в том, что генератор случайных чисел – это, по сути, «черный ящик», и мы не знаем, что происходит внутри него. Если RdRand содержит бэкдор NSA, правительство сможет получить ключи шифрования, которые были сгенерированы с данными, предоставленными этим генератором случайных чисел.
Случайности не случайны, Или как компьютеры генерируют случайные числа
Генератор случайных чисел — это намного сложнее, чем кажется.
Как думаете, что общего в компьютерных гонках, азартных играх и криптографии? На первый взгляд кажется, что ничего. Но на самом деле все они зависят от случайных чисел. От прослушивания музыки до шифрования всего Интернета — случайные числа являются важной частью жизни современного человека. И чаще всего мы полагаемся на компьютеры, которые генерируют их для нас.
Это заставляет задуматься: а как именно компьютеры генерируют случайные числа?
Если вы занимались программированием, то наверняка использовали в своем коде генератор случайных чисел. Для этого в Ruby достаточно вызвать «rand», а в Python — «random ()». Создание ряда случайных чисел может показаться простым. В конце концов числа на компьютере — это набор единиц и нулей. Машине просто нужно случайным образом выбрать 1 или 0 и повторить это столько раз, сколько нужно. Даже мы, люди, можем сделать это легко и просто на листе бумаги.
Однако если копнуть глубже, то мы создали компьютеры, чтобы стать теми, кем не являемся — полностью логическими устройствами. Получается, случайность противоречит их природе. Ну кто захочет, чтобы сервер спонтанно решил не следовать логике приложения?
По своей сути компьютеры — это простые машины, которые принимают данные и выводят их обратно. И чтобы эти машины могли генерировать случайные числа, им нужен внешний источник случайности. Этот источник будет зависеть от того, какой генератор случайных чисел вы захотите использовать. Таких генераторов два — конечно, если говорить об основных.
Первый и самый распространенный тип называется «генератор псевдослучайных чисел (ГПСЧ)». Как следует из названия, он не создает «истинных» случайных чисел. Чтобы сгенерировать с помощью него число, понадобится единственное начальное значение, откуда последует псевдослучайность. Алгоритмы генерации, используемые для ГПСЧ, включают в себя «метод извлечения квадратов», «линейный конгруэнтный метод», «регистр сдвига с линейной обратной связью» и «вихрь Мерсенна».
ГПСЧ автоматически создает длинные серии чисел с хорошими случайными свойствами и делает это быстро и дешево — в этом его преимущества. Но есть и очевидный минус: с ограниченными ресурсами любой ГПСЧ рано или поздно зацикливается и начинает повторять одну и ту же последовательность чисел. Однако чаще всего этот шаблон не воспринимается людьми, что делает ГПСЧ подходящим для использования в видеоиграх и программировании.
Нельзя не сказать о том, что слабым местом ГПСЧ все-таки пользуются: например, любители гонок, которые манипулируют ГСЧ и заставляют игру работать предсказуемо, чтобы пройти ее как можно скорее. Есть случаи, когда предсказание случайных чисел имеет более серьезные последствия. Зная начальное значение, злоумышленник может угадать сгенерированный пароль и получить доступ к личным данным пользователя.
Второй тип генератора — генератор «истинно» случайных чисел (ГИСЧ или TRNG). В качестве внешнего источника случайности он использует энтропию. Не углубляясь в теорию хаоса и термодинамику, отметим, что энтропия — это чистый нефильтрованный хаос. И лучший источник этого хаоса — сам компьютер. Компьютер не может работать случайным образом, чего не скажешь о его составляющих.
Компьютер — это сложная система со множеством движущихся частей и непостоянством, где регулярно возникают тепловой шум, фотоэффект и другие квантовые явления. В конце концов инженеры по аппаратному обеспечению выяснили, что, используя сложную схему аппаратных микросхем и компонентов, компьютеры могут преобразовывать физический шум в цифровые единицы и нули.
Чаще всего ГИСЧ используют в цифровых азартных играх: бросание костей, тасование карт, рулетка — все это завязано на неопределенности. А еще в общественных вопросах, военных призывах и выборе присяжных, где случайность выступает в качестве метода справедливости.
Однако на самом деле спектр использования ГИСЧ тоже ограничен, ведь у него есть свои недостатки. Во-первых, для генерации чисел требуется много времени. А еще ГИСЧ не всегда надежны. Компьютерам требуется достаточное количество энтропии для создания истинных случайных чисел, но случайность заключается в том, что она возникает… случайно! Неактивный или новый сервер не сможет создавать номера такого же высокого качества, как активный.
Поскольку и ГПСЧ, и ГИСЧ имеют свои недостатки, их можно без проблем использовать в гейм-сфере и азартных играх, но нельзя — в криптографии, которая требует высокой безопасности. По этой причине появился гибридный тип — «криптографически стойкий генератор псевдослучайных чисел (КСГПЧ или CSPRNG)», который обладает скоростью ГПСЧ и безопасностью ГИСЧ.
КСГПЧ — это генератор, использующий высококачественный источник энтропии для создания начального числа. Затем оно вводится в алгоритм, который производит случайные и безопасные числа. Проще говоря, он использует ГИСЧ для создания начального числа для ГПСЧ. Если все сделано правильно, КСГПЧ гарантирует, что начальное число действительно случайно, а полученный результат нельзя взломать или реконструировать. Обычно его используют в операционных системах вроде Unix и Linux.
Тем не менее, даже несмотря на преимущества КСГПЧ, как и всего остального в технологической индустрии, абсолютная безопасность недостижима.
Теперь, когда в следующий раз вы будете играть в видеоигру, слушать музыку в случайном порядке или просто генерировать случайное число в своем коде, вы осознаете всю магию, которая творится «под капотом».
Как компьютер генерирует случайные числа
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
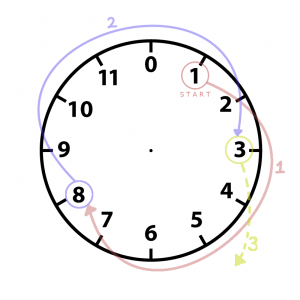
Числовой круг
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали «прыжки» за счёт добавления, но что если использовать умножение? Умножим х на константу a.
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
Подробно о генераторах случайных и псевдослучайных чисел
Введение
Как отличить случайную последовательность чисел от неслучайной?
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
Экспоненциальное распределение
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
Краеугольный камень псевдослучайности: с чего начинается поиск чисел

(с)
Случайные числа постоянно генерируются каждой машиной, которая может обмениваться данными. И даже если она не обменивается данными, каждый компьютер нуждается в случайности для распределения программ в памяти. При этом, конечно, компьютер, как детерминированная система, не может создавать истинные случайные числа.
Когда речь заходит о генераторах случайных (или псевдослучайных) чисел, рассказ всегда строится вокруг поиска истинной случайности. Пока серьезные математики десятилетиями ведут дискуссии о том, что считать случайностью, в практическом отношении мы давно научились использовать «правильную» энтропию. Впрочем, «шум» — это лишь вершина айсберга.
С чего начать, если мы хотим распутать клубок самых сильных алгоритмов PRNG и TRNG? На самом деле, с какими бы алгоритмами вы не имели дело, все сводится к трем китам: seed, таблица предопределенных констант и математические формулы.
Каким бы ни был seed, еще есть алгоритмы, участвующие в генераторах истинных случайных чисел, и такие алгоритмы никогда не бывают случайными.
Что такое случайность
Первое подходящее определение случайной последовательности дал в 1966 году шведский статистик Пер Мартин-Лёф, ученик одного из крупнейших математиков XX века Андрея Колмогорова. Ранее исследователи пытались определить случайную последовательность как последовательность, которая проходила все тесты на случайность.
Основная идея Мартина-Лёфа заключалась в том, чтобы использовать теорию вычислимости для формального определения понятия теста случайности. Это контрастирует с идеей случайности в вероятности; в этой теории ни один конкретный элемент пространства выборки не может быть назван случайным.
«Случайная последовательность» в представлениях Мартина-Лёфа должна быть типичной, т.е. не должна обладать индивидуальными отличительными особенностями.
Было показано, что случайность Мартина-Лёфа допускает много эквивалентных характеристик, каждая из которых удовлетворяет нашему интуитивному представлению о свойствах, которые должны иметь случайные последовательности:
Существование множественных определений рандомизации Мартина-Лёфа и устойчивость этих определений при разных моделях вычислений свидетельствуют о том, что случайность Мартина-Лёфа является фундаментальным свойством математики.
Seed: основа псевдослучайных алгоритмов
Первые алгоритмы формирования случайных чисел выполняли ряд основных арифметических действий: умножить, разделить, добавить, вычесть, взять средние числа и т.д. Сегодня такие мощные алгоритмы, как Fortuna и Yarrow (используется в FreeBSD, AIX, Mac OS X, NetBSD) выглядят как генераторы случайных чисел для параноиков. Fortuna, например, это криптографический генератор, в котором для защиты от дискредитации после выполнения каждого запроса на случайные данные в размере 220 байт генерируются еще 256 бит псевдослучайных данных и используются в качестве нового ключа шифрования — старый ключ при этом каждый раз уничтожается.
Прошли годы, прежде чем простейшие алгоритмы эволюционировали до криптографически стойких генераторов псевдослучайных чисел. Частично этот процесс можно проследить на примере работы одной математической функции в языке С.
Функция rand () является простейшей из функций генерации случайных чисел в C.
В этом примере рандома используется вложенный цикл для отображения 100 случайных значений. Функция rand () хороша при создании множества случайных значений, но они являются предсказуемыми. Чтобы сделать вывод менее предсказуемым, вам нужно добавить seed в генератор случайных чисел — это делается с помощью функции srand ().
Seed — это стартовое число, точка, с которой начинается последовательность псевдослучайных чисел. Генератор псевдослучайных чисел использует единственное начальное значение, откуда и следует его псевдослучайность. Генератор истинных случайных чисел всегда имеет в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
srand() принимает число и ставит его в качестве отправной точки. Если seed не выставить, то при каждом запуске программы мы будем получать одинаковые случайные числа.
Вот пример простой формулы случайного числа из «классики» — книги «Язык программирования C» Кернигана и Ричи, первое издание которой вышло аж в 1978 году:
Эта формула предполагает существование переменной, называемой random_seed, изначально заданной некоторым числом. Переменная random_seed умножается на 1 103 535 245, а затем 12 345 добавляется к результату; random_seed затем заменяется этим новым значением. Это на самом деле довольно хороший генератор псевдослучайных чисел. Если вы используете его для создания случайных чисел от 0 до 9, то первые 20 значений, которые он вернет при seed = 10, будут такими:
Если у вас есть 10 000 значений от 0 до 9, то распределение будет следующим:
0 — 10151 — 10242 — 10483 — 9964 — 9885 — 10016 — 9967 — 10068 — 9659 — 961
Любая формула псевдослучайных чисел зависит от начального значения. Если вы предоставите функции rand() seed 10 на одном компьютере, и посмотрите на поток чисел, которые она производит, то результат будет идентичен «случайной последовательности», созданной на любом другом компьютере с seed 10.
К сожалению, у генератора случайных чисел есть и другая слабость: вы всегда можете предсказать, что будет дальше, основываясь на том, что было раньше. Чтобы получить следующее число в последовательности, мы должны всегда помнить последнее внутреннее состояние генератора — так называемый state. Без state мы будем снова делать одну и ту же математическую операцию с одинаковыми числами, чтобы получить тот же ответ.
Как сделать seed уникальным для каждого случая? Самое очевидное решение — добавить в вычисления текущее системное время. Сделать это можно с помощью функции time().
Функция time() возвращает информацию о текущем времени суток, значение, которое постоянно изменяется. При этом метод typecasting гарантирует, что значение, возвращаемое функцией time(), является целым числом.
Итак, в результате добавления «случайного» системного времени функция rand() генерирует значения, которые являются более случайными, чем мы получили в первом примере.
Однако в этом случае seed можно угадать, зная системное время или время запуска приложения. Как правило, для приложений, где случайные числа являются абсолютно критичными, лучше всего найти альтернативное решение.
Но опять же, все эти числа не случайны.
Лучшее, что вы можете сделать с детерминированными генераторами псевдослучайных чисел — добавить энтропию физических явлений.
Период (цикл) генератора
Одними из наиболее часто используемых методов генерации псевдослучайных чисел являются различные модификации линейного конгруэнтного метода, схема которого была предложена Дерриком Лемером еще в 1949 году:
Рассмотрим случай, когда seed равен 1, а период — 100 (на языке Haskell):
В результате мы получим следующий ответ:
Это лишь пример и подобную структуру в реальной жизни не используют. В Haskell, если вы хотите построить случайную последовательность, можно воспользоваться следующим кодом:
Выбор случайного Int дает вам обратно Int и новый StdGen, который вы можете использовать для получения более псевдослучайных чисел. Многие языки программирования, включая Haskell, имеют генераторы случайных чисел, которые автоматически запоминают свое состояние (в Haskell это randomIO).
Чем больше величина периода, тем выше надежность создания хороших случайных значений, однако даже с миллиардами циклов крайне важно использовать надежный seed. Реальные генераторы случайных чисел обычно используют атмосферный шум (поставьте сюда любое физическое явление — от движения мыши пользователя до радиоактивного распада), но мы можем и схитрить программным методом, добавив в seed асинхронные потоки различного мусора, будь то длины интервалов между последними heartbeat потоками или временем ожидания mutual exclusion (а лучше добавить все вместе).
Истинная случайность бит
Итак, получив seed с примесью данных от реальных физических явлений (либо максимально усложнив жизнь будущему взломщику самым большим набором потоков программного мусора, который только сможем придумать), установив state для защиты от ошибки повтора значений и добавив криптографических алгоритмов (или сложных математических задач), мы получим некоторый набор данных, который будем считать случайной последовательностью. Что дальше?
Дальше мы возвращаемся к самому началу, к одному из фундаментальных требований — тестам.
Национальный институт стандартов и технологий США вложил в «Пакет статистических тестов для случайных и псевдослучайных генераторов чисел для криптографических приложений» 15 базовых проверок. Ими можно и ограничиться, но этот пакет вовсе не является «вершиной» проверки случайности.
Одни из самых строгих статистических тестов предложил профессор Джордж Марсалья из Университета штата Флорида. «Тесты diehard» включают 17 различных проверок, некоторые из них требуют очень длинных последовательностей: минимум 268 мегабайт.
Случайность можно проверить с помощью библиотеки TestU01, представленной Пьером Л’Экуйе и Ричардом Симардом из Монреальского университета, включающей классические тесты и некоторые оригинальные, а также посредством общедоступной библиотеки SPRNG.
Еще один полезный сервис для количественного измерения случайности.