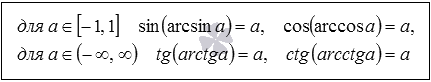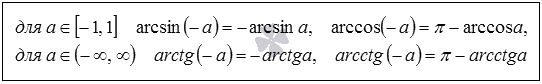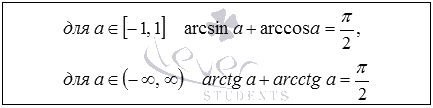Как косинус перевести в арктангенс
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.
В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.
Навигация по странице.
Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.
Синус арксинуса, косинус арккосинуса и т.п.
Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Арксинус синуса, арккосинус косинуса и т.п.
Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.
Связи между arcsin, arccos, arctg и arcctg противоположных чисел
Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.
Синус от арккосинуса, тангенс от арксинуса и иже с ними
На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.
Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид 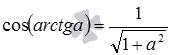
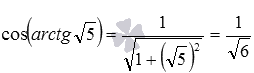
Другой пример: используя формулу синуса арккосинуса вида 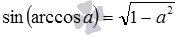
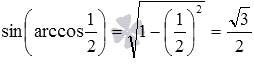
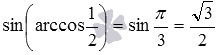
Осталось показать вывод записанных формул.
Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.
Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств 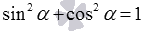
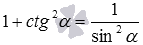
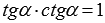
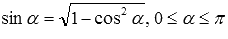
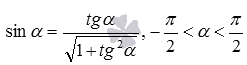
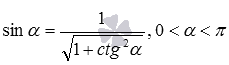
Вот краткая запись вышеперечисленных выкладок:
По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:
Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:
Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как 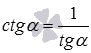
arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.
По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:
Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:
Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:
Наконец, вот ряд формул с арккотангенсом:
Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.
Для примера, докажем, что 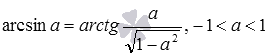
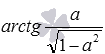
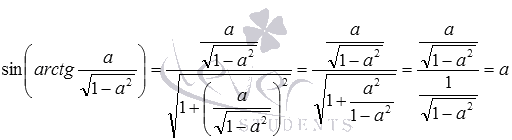
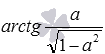
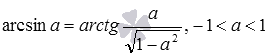
По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.
В данном примере мы могли вычислить требуемое значение и непосредственно: 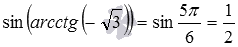
Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида 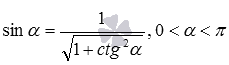
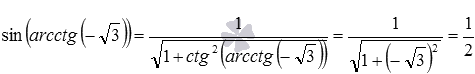
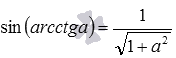
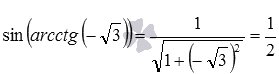
Некоторые другие формулы
Узнать ещё
Знание — сила. Познавательная информация
cos (arctg x)
С помощью определения косинуса и тангенса в прямоугольном треугольнике, а также определения арктангенса и теоремы Пифагора найти косинус арктангенса cos (arctg x) можно быстро, не привлекая дополнительные тригонометрические формулы.
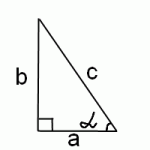
Тангенс угла альфа в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему:
Нам нужно найти косинус этого же угла альфа. Поскольку косинус альфа равен отношению прилежащего катета к гипотенузе
остается найти гипотенузу. По теореме Пифагора
1) Найти cos (artg (3/4)).
Поскольку тангенс альфа — это отношение противолежащего катета к прилежащему, то противолежащий катет b=3, прилежащий катет a=4. Нам нужно найти косинус этого же угла альфа. Так как косинус равен отношению прилежащего катета к гипотенузе, находим по теореме Пифагора гипотенузу
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
Теперь разберем примеры, как они применяются в задачах.
Решение
У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2
Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6
Решение
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
sin 2 α + cos 2 α = 1 1 + c t g 2 α = 1 sin 2 α
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
Следовательно, sin ( a r c t g α ) = t g ( a r c t g α ) 1 + t g 2 ( a r c t g α ) = α 1 + α 2
Следовательно, sin ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
следует, что cos ( a r c t g α ) = c t g ( a r c c t g α ) 1 + c t g 2 ( a r c c t g α ) = α 1 + α 2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
А так мы выразим арккосинус через остальные обратные функции:
Формула выражения арктангенса:
Последняя часть – выражение арккотангенса через другие обратные функции:
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Решение
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.