Как можно построить прямой угол
10 способов построения прямого угла
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
муниципальное общеобразовательное учреждение
«Средняя школа с углубленным изучением
№ 57 Кировского района Волгограда»
построения прямого угла
Подготовили ученицы 5 «А» класса
Рябцева Вероника, Парамонова Арина
Построение прямого угла с использованием транспортира
Часто снег идет зимой
И приносит радость,
Угол помните прямой 90 градусов!
Построение прямого угла с использованием угольника
Кому не приятна за труд похвала
Разгонит, которая тучи.
Развернутый угол дели пополам
Прямые углы ты получишь.
Построение прямого угла с использованием подручных предметов
прямые углы повсюду нас окружают!
4.Построение прямого угла с использованием египетского треугольника
Завяжите на веревке 2 узелка. Это первый отрезок. Согните веревку и отложите равный первому отрезок, завяжите узелок, получили 3 узелка и 2 равных отрезка. Продолжите до получения 12 равных отрезков узелками. Если натянуть эту веревку так, чтобы она образовала тре угол ьник со сторонами в 3, 4 и 5 промежутков, то угол напротив самой длинной стороны будет прямым!
А почему египетский треугольник?
Построение прямого угла с использованием клочка бумаги или ткани
Вы догадались, что никакого фокуса здесь нет. Сгибая клочок первый раз, мы получили развернутый угол. Согнув второй раз, разделили развернутый угол пополам, а это и есть прямой угол! 5
Построение прямого угла с использованием грузика
Груз, подвешенный на нити, за счет силы тяжести всегда перпендикулярен поверхности земли (поверхность земли, подразумевается без уклонов, впадин).
Построение прямого угла с использованием понятия «кратчайшее расстояние»
Оказывается, кратчайший путь от точки до прямой, проходит под прямым углом к заданной прямой!
Потренируйтесь, строить от руки прямые углы. Измерьте полученные углы, оцените свой глазомер.
Построение прямого угла с использованием свойства диагоналей ромба
Почему так происходит?
Разрежьте ромбик по диагоналям на 4 части, сложите из них 2 «прямоугольника». Сомневаетесь, что эти фигуры действительно прямоугольники.
Построение прямого угла с использованием окружности
Затем проводим диаметр. Отмечаем на окружности любую точку. Соединяем концы диаметра с точкой окружности. Полученный треугольник прямоугольный! А значит, прямой угол построен.
Построение прямого угла с использованием циркуля и линейки
Наверное, кто то скажет, что одни способы построения прямого угла более точные, чем другие. Не торопитесь с выводами!
Построение прямого угла с использованием транспортира, на первый взгляд, обеспечивает точное построение прямого угла. Однако, любой прибор имеет погрешность измерения равное одному делению шкалы, и транспортир не исключение. Отклонение в 1 ̊, кажется, несущественным. А известна ли нам погрешность других способов? Возможно, их погрешность также не превышает 1 ̊.
Неоспоримое преимущество некоторых способов построения прямого угла в минимуме необходимых приспособлений. Ведь, в природе редко встречается прямой угол. Окажись, вдали от цивилизации Вы, в случае необходимости, достаточно точно построите прямые углы.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-028523
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Более 50 российских школ перешли на дистанционку из-за коронавируса
Время чтения: 1 минута
В Хабаровском крае введут уроки по вакцинации в некоторых школах и колледжах
Время чтения: 1 минута
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Три варианта построения прямого угла на местности. Как проверить угол уже построенного дома, когда замер диагоналей невозможен?
В данной статье описываются три распространенных варианта построения прямых углов при разметке участка для будущего дома, а также описываются методы проверки углов уже возведенных зданий и сооружений без доступа к замеру их диагоналей.
На самом же деле, вариантов существует множество и большинство из них выражаются через тригонометрические функции или с помощью сложных геометрических построений, но здесь это ни к чему, на стройплощадке ни один строитель не возьмется за сложные вещи, упуская время.
Поэтому, рассмотрим три самых простых, но тем не менее надежных метода построения прямых углов:
Теорема Пифагора
Это самый часто используемый и очень надежный способ.
Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника и звучит так: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Для построения прямого угла можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома, можно без труда вычислить значение диагонали для своего дома и в дальнейшем работать с полученным значением.
Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Для удобства, существуют производные треугольники от основного, получаемые при умножении сторон треугольника Пифагора на какой-либо коэффициент. К примеру, стороны 3,4,5 умноженные на К=2 (коэффициент 2), дают треугольник со сторонами 6,8,10, при К=3, стороны 9,12,15 и т.д.
Геометрическое построение
Данный способ ни чуть не хуже Пифагорова треугольника, но редко используемый (в силу забывчивости школьных знаний), хотя очень даже эффективный!
Выглядит сложнее, чем на самом деле.
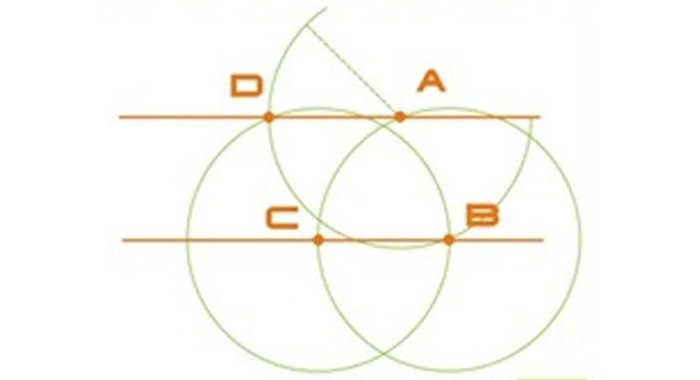
Зная угол здания (точка О), отмечаем две точки О1 и О2 по оси А, равноудаленные от точки О. Одинаковое расстояние откладывается с помощью рулетки.
Точки О1 и О2 являются центрами окружностей одинакового радиуса. Прямая, проведенная через точку пересечения двух окружностей (точка В) и точку О будет давать прямой угол с прямой А.
По факту, этот способ ни чуть не хуже треугольника Пифагора, имея под рукой два колышка и отрезок веревки, построение осей будущего дома производится всего за 20-40 минут в зависимости от размера и сложности здания.
Две рулетки
Вместо построения окружностей из точек О1 и О2, используются две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и прикладываются нулевой отметкой к каждой из точек О1 и О2.
Далее, совмещаем их одинаковыми значениями по мерным шкалам (точка Х) и получаем точку Х, соединив которую с точкой О получим перпендикуляр. В данном случае, построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.
На практике это делается следующим образом: отмечается три контрольные точки по двум рулеткам на пересечении делений (к примеру 1 м., 3м. и 7м.). Далее, через них протягивается разметочный шнур из точки О. Если все точки пересечения шкал лежат на одной прямой (совпадают со шнуром), то построение выполнено верно.
Это настолько быстро делается, что на первый взгляд может показаться неправдоподобным, но поверьте — геометрия работает со 100% гарантией.
Проверка прямого угла построенного здания
Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется сооружать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.
Все действия аналогичны и главное правило заключается в том, чтобы вынести замеры за пределы строения.
Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками, а после — снимаем замер.
При геометрическом построении, точка пересечения двух окружностей будет лежать не в основании стены, а по «невидимому» продолжению стены в её же плоскости (на рисунке обозначена точкой Х).
При необходимости, все способы свободно комбинируются или взаимозаменяются.
На этом всё, спасибо Вам за уделенное внимание!
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:
Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.
Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.
Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?
Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?
На чертеже противоположные стороны обозначены одинаковым цветом.
Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.
Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.
Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».
Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:
Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
Ставим точку. Откладываем два луча при помощи угольника или линейки.
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.
До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
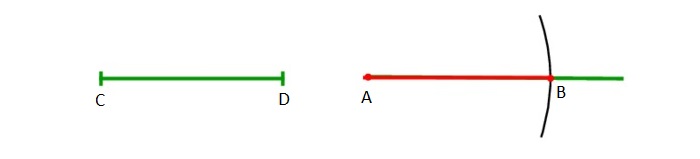
Построение отрезка, равного данному
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
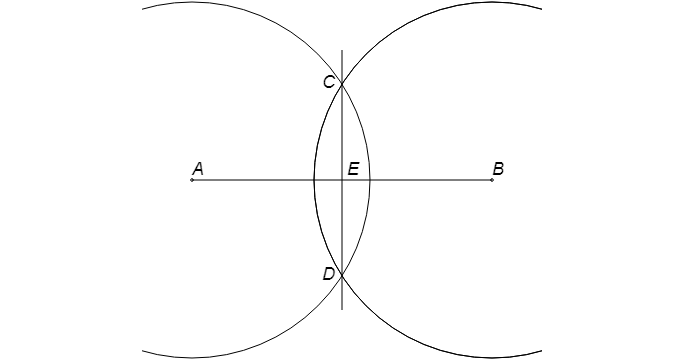
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
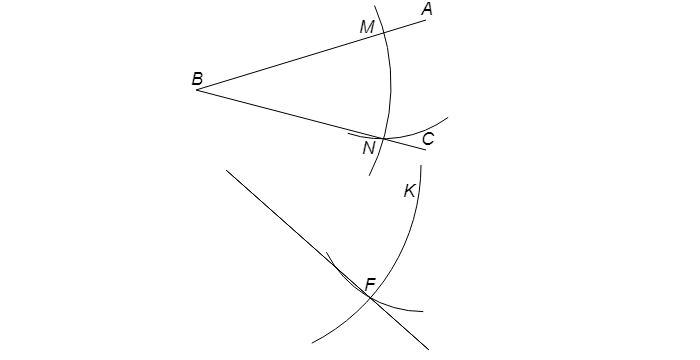
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
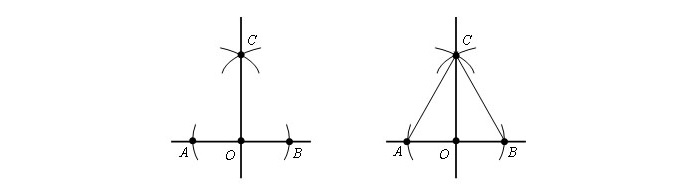
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
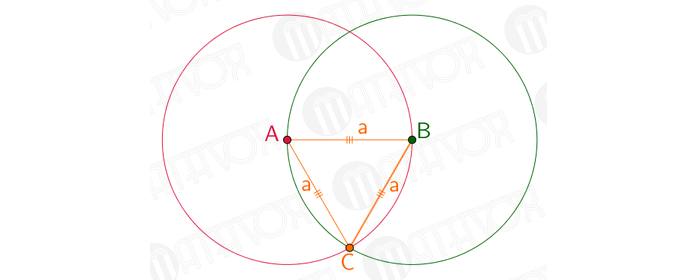
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
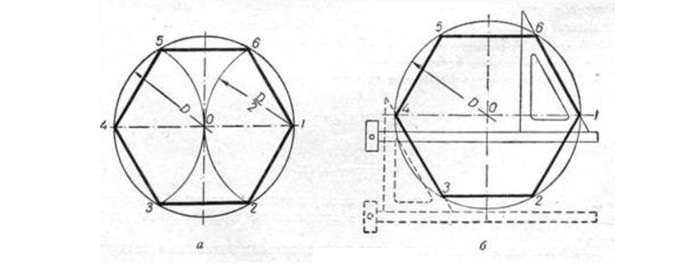
Построение правильного четырехугольника вписанного в окружность
Вариант 1
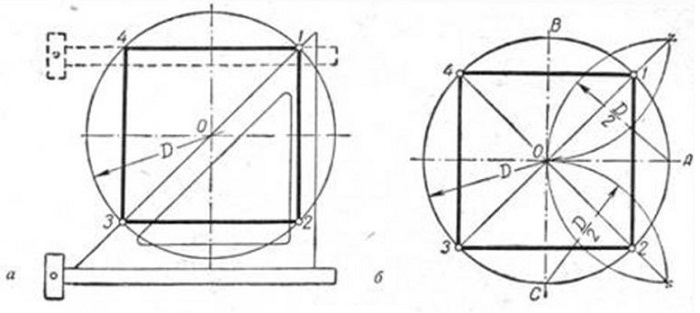
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
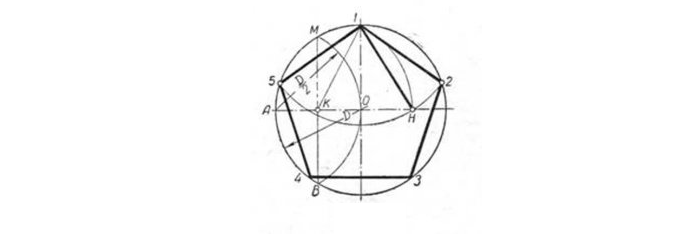
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.