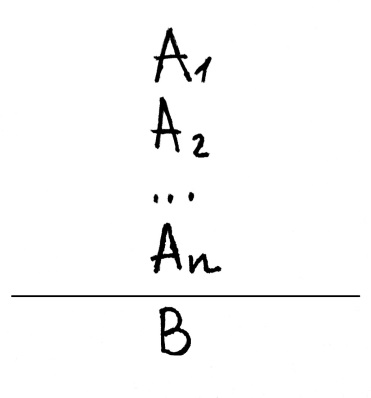Как можно проверить истинность утверждения
Как можно проверить утверждение на истинность?
Соответствием реальным фактам, отсутствием фактов против, возможностям делать проверяемые, неочевидные выводы. Ну и логика тоже хороший инструмент.
Есть разные методы. Например-аксиома, она просто принимается без доказательств.
Потом есть уверенность-2х2=4,с этим не поспорить.
Проверяемость-повторение того, что сказали опытным путем.
Методичность. Ищем метод, которым можно проверить.
Ну и допускаемость-типа «в принципе это возможно».
Если оно что то объясняет в нашей жизни, то логика есть, чем больше объясняет, тем больше логик иа до истинности пам очень далеко, только отдельные аспекты
Есть ли какие либо реальные критерии оценки истинности. Да есть. В самом общем смысле это, прогноз будущего информационного сосотояния системы. Проще говоря если некой группе людей предложить ответить на вопрос, «что будет если. » Выслушить каждого а затем реализовать это «если» и посмотреть что получились. Ближе всех к истине будет тот, чей теоретический прогноз в большей степени совпал с реальностью. Если Вам итересно моё более расширенное мнение по данному вопросу, посмотрите «Теорию системных миров» раздел «О истине»
Урок 6. Умозаключения

Содержание:
Умозаключение – это непосредственный переход от одного или нескольких высказываний А1, А2, …, Аn к высказыванию В. А1, А2, …, Аn называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.
В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:
Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»
Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.
Логики записывают умозаключения следующим образом:
Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.
Критерии истинности умозаключений
Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.
Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:
Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.
Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.
Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.
Умозаключения по логическому квадрату
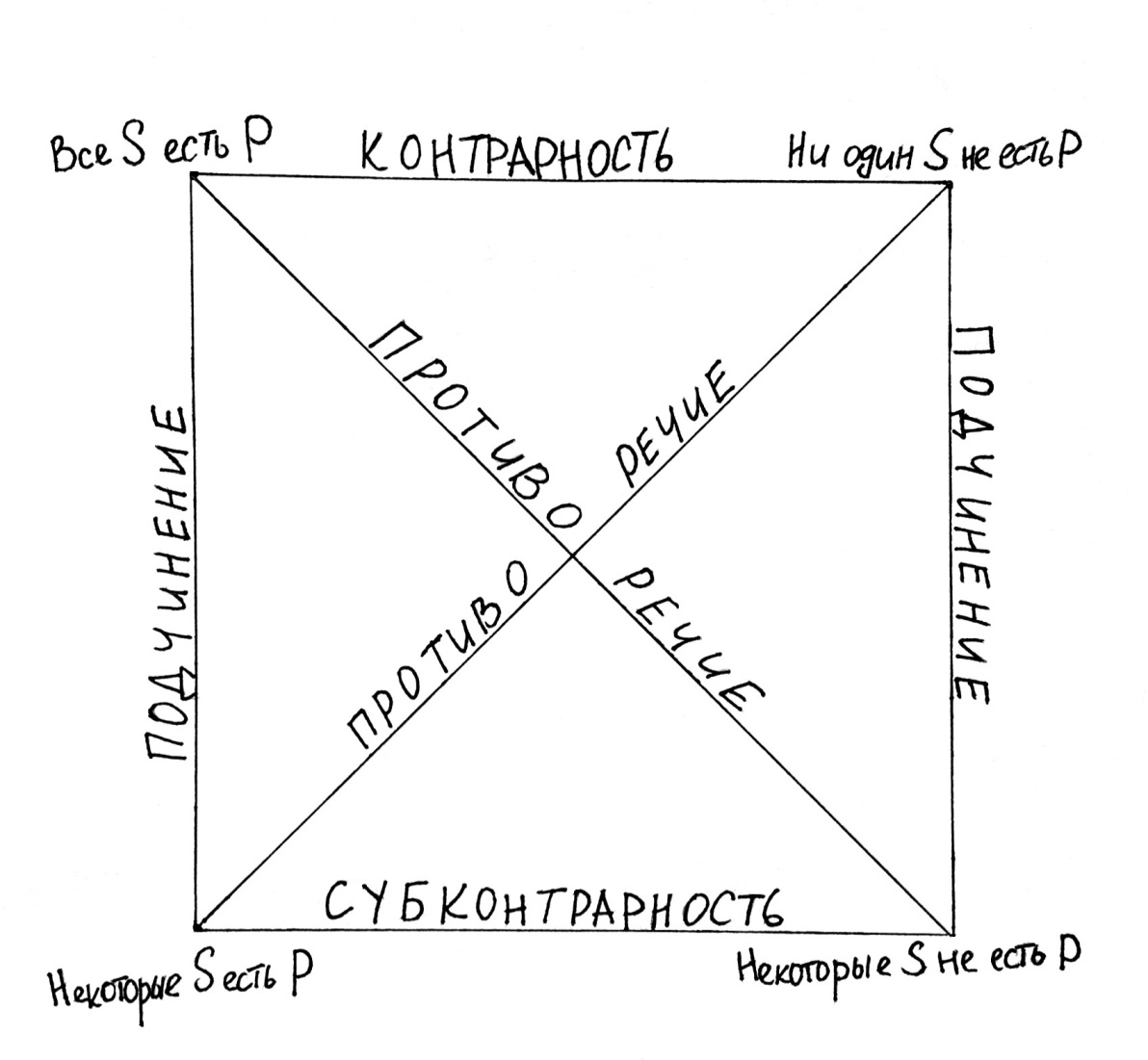
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:
Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:
Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:
Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.
По закону контрарного противоречия будут истинными следующие виды умозаключений:
Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.
Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.
На этих законах строятся умозаключения следующих видов:
Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.
Операция обращения
Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.
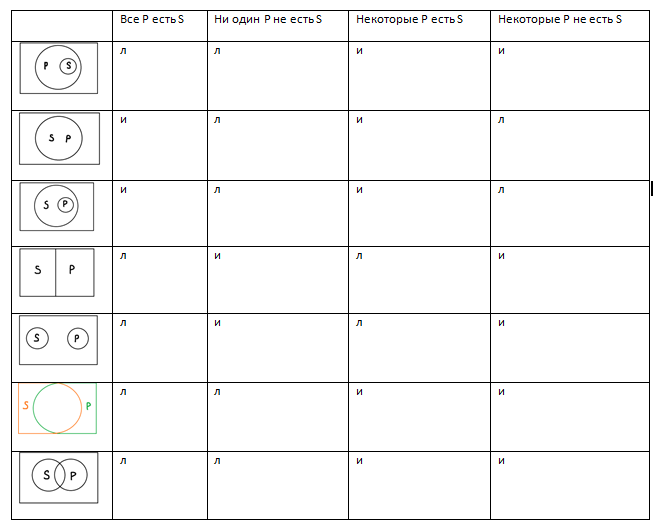
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.
Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.
Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:
Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.
Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.
Упражнение «Подберите ключ»
В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:
Сделайте обращения с теми, высказываниями, с которыми это возможно:
Проверьте, правильно ли сделаны следующие умозаключения:
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Построить таблицу истинности следующих логических выражений
Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.
Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.
Алгебраические преобразования логических выражений
Отрицание
Таблица истинности для отрицания будет такова:
| А | не А |
| Л | И |
| И | Л |
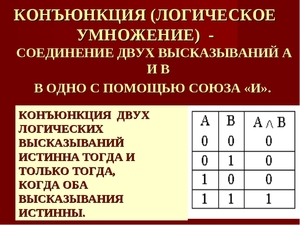
Конъюнкция
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| И | Л | Л |
| И | И | И |
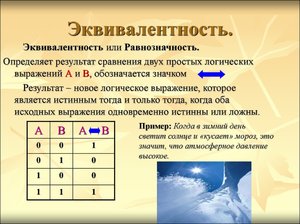
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
Построение таблиц истинности
Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:
В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.
Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:
Примеры
Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:
Штрих Шеффера
| А | Б | А и Б | не (А и Б) |
| Л | Л | Л | И |
| Л | И | Л | И |
| И | Л | Л | И |
| И | И | И | Л |
Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
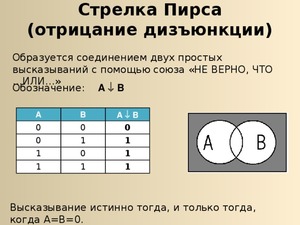
Стрелка Пирса
Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:
| А | Б | А или Б | не (А или Б) |
| Л | Л | Л | И |
| Л | И | И | Л |
| И | Л | И | И |
| И | И | И | Л |
| А | Б | не А | не Б | не А и не Б |
| Л | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | И |
| И | И | Л | Л | Л |
Определение эквивалентности
Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».
Здесь две переменных и пять действий. Строим таблицу:
| А | Б | В = (из А следует Б) | Г = (из Б следует А) | Д = А эквивалентно Б | Е = В и Г | Д эквивалентно Е |
| Л | Л | И | И | И | И | И |
| Л | И | И | Л | Л | Л | И |
| И | Л | Л | И | Л | Л | И |
| И | И | И | И | И | И | И |
В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
Критерии истины. Способы проверки истины.



Под критерием истины понимается разрешающая процедура, позволяющая оценивать знание либо как истинное, либо как ложное. Если пытаться искать такую процедуру исключительно внутри самого знания, то возникает парадокс, схваченный в свое время еще Секстом Эмпириком: для нахождения такого критерия нужен, в свою очередь, критерий, и так до бесконечности.
Практика как критерий истины. Безусловной заслугой марксизма является то, что он в ясной и недвусмысленной форме постарался найти критерий истины не внутри системы знания, а вне ее — в общественно-исторической практике человека. «В практике, — писал К. Маркс, — должен доказать человек истинность, т.е. действительность и мощь, посюсторонность своего мышления». В самом деле, наиболее действенная проверка объективной укорененности наших идей и теоретических моделей в структурах мирового бытия возможна в том случае, если нечто практически (телесно) созданное на их идеальной основе проходит испытание на свою функциональную пригодность в рамках этого мирового целого.
Успешная объективация (или, грубо говоря, материализация) наших знаний в технических устройствах, хозяйственной и социальной деятельности — серьезное свидетельство в пользу того, что мы ничего субъективно не измыслили, а познали нечто объективно сущее и значимое. Так, если ракета не падает, а взлетает в небо — это практическое свидетельство истинности наших физических представлений о законах гравитации; если стиральный порошок отстирывает грязь, — значит, наши сведения о протекании химических реакций в природе правильны; если мы ведем успешную социальную политику, избегая конфронтации в обществе и способствуя росту его духовных запросов, значит, наши социологические представления верны
Эмпирические критерии истины. Формой научного проявления критерия практики является эксперимент, т.е. строго описанная и желательно техническая воспроизводимая процедура проверки опытных (эмпирических) следствий, выводимых из какой-либо теории.
Одним из таких эмпирических критериев (разрешающих процедур) служит верифицируемость теории, т.е. заключение об ее истинности на основании практического подтверждения выведенных из нее опытных следствий. (верификация (лат. verus-истинный и facere — делать) — один из способов проверки истинности теоретических утверждений (гипотез, теорий) путем сопоставления их содержания с содержанием полученных в результате опыта эмпирических данных) Процедура верификации была детально методологически осмыслена в неопозитивистской традиции и даже квалифицировалась как универсальный критерий научности знания. Однако со времен Д. Юма известно, что любой индуктивный вывод носит вероятностный характер (за исключением случаев полной индукции), а потому никакая верифицируемость не может считаться надежной. Один-единственный отрицательный результат эксперимента поставит под сомнение истинность целой теории.
Это и дало основание К. Попперу сформулировать противоположный эмпирический критерий фальсифицируемости, нацеленный не на подтверждение, а, наоборот, на опровержение теоретической модели через опровержение (фальсификацию) выводимых из нее эмпирических следствий. Обе эти процедуры успешно используются в науке.
(Если верификация — это подтверждение истины, то фальсификация — ее искажение. Хотя процедуры верификации и фальсификации зародились в рамках естествознания, формировались по поводу решения естественно-научных задач, рассчитаны на математический аппарат естествознания, они с успехом применяются и в социологии. Этим мы обязаны американским социологам — представителям количественной методологии, научная школа которых существовала в 20—30-е гг. XX в.
Фальсификация предполагает, что ученый вместо поиска всех примеров, подтверждающих гипотезу, обнаруживает один-единственный случай, опровергающий ее. Тут все как в жизни: надо доказать ложность гипотезы или теории с помощью единичного факта, а не искать всех ворон на Земле ради подтверждения истины. Если вы утверждаете, что все вороны черные, вам достаточно найти одну белую ворону и доказать ее исключительность — тогда вы получите право сказать, что, за редким исключением, все вороны черные.
Оказывается, опровергать гипотезу намного проще и экономичнее, чем ее подтверждать. Если вы утверждаете, что любая социальная группа имеет свою субкультуру, то вы должны либо пересчитать все большие социальные группы (пенсионеров, молодежь, национальные меньшинства, профессиональные группы и т.д.) и доказать, что у каждой есть своя субкультура, либо найти среди них такую, у которой нет своей субкультуры, и сказать, что есть единственная большая социальная группа, которую можно назвать исключением из правил. В первом случае речь идет о верификации, во втором — о фальсификации.)
Однако критерий практики и в ее общественно-историческом, и в научно-экспериментальном проявлении не может считаться достаточным. В науках, особенно дедуктивных, существует масса теоретических идей и гипотез, которые нельзя проверить не только ни в какой практической деятельности, но даже в эксперименте. Более того, абсолютизация критерия практики может быть смертельно опасной для существования науки. В истории уже были случаи, когда требование немедленных практических и экспериментальных результатов служило оправданием идеологического давления на науку. Так, под лозунгом отсутствия реальных практических приложений в 40—50-х гг. XX в. у нас травили генетику, позднее — кибернетику. Все это заставляет искать критерии истины уже не вне, а внутри самой науки, позволяющей ей существовать в качестве относительно автономной и самоценной сферы духовного творчества человека.
Логические критерии. Важнейшим их них является логическая непротиворечивость, т.е. запрет на одновременное наличие суждений А и не-А внутри научной гипотезы или теории. Формально-логическая противоречивость означает, что теория абсолютно не информативна, ибо из противоречия следует все, что угодно, — бесконечный универсум суждений.
Другой важный логический критерий истины — критерий независимости аксиом, т.е. невыводимость одних исходно принятых допущений (аксиом, постулатов) теории из других. Обнаружение факта нарушения этого принципа — серьезное свидетельство в пользу ошибочности данной теории
Кроме этого выделяют еще критерий полноты теории. Семантическая полнота означает, что все суждения внутри данной теоретической модели являются доказанными, а не произвольно введенными. Критерий синтаксической полноты гласит, что теория является истинной (или, точнее, корректной), если присоединение к ней произвольного суждения (формулы) делает ее противоречивой. Логические критерии истины, во-первых, носят достаточно формальный и отрицательный характер (т.е. свидетельствуют не столько об истине, сколько об ошибочности каких-либо теоретических представлений) и, во-вторых, за исключением универсального критерия непротиворечивости имеют актуальное значение в основном для аксиоматически построенных теорий в логике и математике.
Специфицированные теоретические критерии. В естественных и обществоведческих, а отчасти и гуманитарных, науках используется целый спектр собственно теоретических критериев истины.
Одним из них является критерий внутренней и внешней когерентности знания, т.е. требование системной упорядоченности и взаимосогласованности положений внутри самой теории (гипотезы), а также желательность ее согласования с фундаментальным и непроблематизируемым знанием в науке. Так, если какая-то теоретическая гипотеза в физике противоречит закону сохранения энергии, то это — веское основание для констатации ее ложности.
Другим важным теоретическим критерием истины является принцип простоты теории. Он означает, в частности, что из двух конкурирующих в науке гипотез скорее всего будет избрана та, которая решает проблему наиболее экономным и рациональным способом: использует меньшее количество исходных аксиом при том же объяснительном и предсказательном потенциале; опирается на более простой математический аппарат; не привлекает сложной терминологии и т.д.
Например, в истории квантовой механики при описании поведения элементарной частицы конкурировали подходы В. Гейзенберга и Э. Шредингера. Победу одержали идеи Шредингера именно по критерию простоты: его математическое уравнение волновой функции было намного проще сложнейшего математического аппарата, привлеченного Гейзенбергом.
Красота как критерий истины. Наконец, в науке используется и этот критерий, пожалуй, наименее прозрачный и рациональный, но часто оказывающийся решающим в ситуации выбора.
Данный критерий, несмотря на кажущуюся его отдаленность от науки и вообще рационального познания, на самом деле присущ любому виду деятельности людей и носит фундаментальный характер. Это было глубоко понято уже в античности. Античная культура не только в искусстве, но также в науке и философии была ориентирована на незаинтересованное эстетическое наслаждение. Эстетическое наслаждение — это особого рода чувствительность к красоте, прекрасному, изначально заложенная в каждом человеке. Эта чувствительность, по мысли древнего грека, распространяется на все формы человеческого бытия и творчества. Отсюда становится понятным и название грандиозного замысла лосевской «Истории античной эстетики», которая представляет собой не просто историко-эмпирический анализ всего многообразия эстетических концепций античности, а историко-теоретическое осмысление античной философии и культуры в целом, взятой в ее самом существенном аспекте.
Красота для древнего грека — это универсальная характеристика взаимоотношений между человеком и миром. Человек не только ищет свое место в структуре бытия, чем занимается онтология. Он не только познает мир, чем занимается гносеология. Он этим миром и добытым знанием о нем способен искренне восхищаться и наслаждаться. Бытие и знание изначально эстетичны, а стало быть, и истина, и сам ее поиск должны быть прекрасными. Об этом четко говорил уже Платон. Закон, открываемый математикой или философией, — это одно из проявлений мировой гармонии, а поэтому и познание этих законов есть действо эстетическое. Для человека античной культуры нет ничего особенного в выражениях типа «эта теория прекрасна» или «я наслаждался его аргументацией».
Отсюда и несколько иное понятие искусства, а точнее, искусства как части общего предмета эстетики. Это не просто некая совокупность знаний об искусстве и его видах, а искусство как деятельность, т.е. скорее ремесло, умение. Речь идет об умении так использовать наши знания, так владеть ими, что этим также можно наслаждаться и восхищаться. Это умение, доведенное до высшей степени совершенства. Отсюда и диалектика как искусство спора и геометрия как искусство измерения земли, и эристика как искусство спора. Поэтому «подлинное искусство для Платона — это сама жизнь, но жизнь методически устроенная и научно организованная»
Это, восходящее к античности, органичное сближение искусства и научного творчества никогда не умирает в последующей культуре. Многие крупные ученые в первую очередь ориентировались и ориентируются именно на эстетический критерий красоты теории.
Например, основной прием, которым Эйнштейн руководствовался, было стремление выразить закон тяготения в наиболее изящной математической форме. Именно это стремление и привело его к понятию о кривизне пространства. Основная мощь теории тяготения Эйнштейна заключается в ее исключительной внутренней математической красоте.
Известно, что, формулируя свои законы движения планет Солнечной системы, И. Кеплер изначально пытался вписать их в систему правильных платоновских многогранников из диалога «Тимей». Эстетический критерий гармонии, изящества, завершенности научных построений оказывается особенно популярным среди логиков, математиков и представителей естественных наук, хотя он не чужд ученым и из других отраслей знания. Все это свидетельствует, с одной стороны, о недопустимости жесткого противопоставления друг другу различных форм рационального постижения бытия, а с другой — о глубинной связи рациональных и внерациональных видов опыта, как это видно из деятельности того же И. Кеплера, работ средневековых алхимиков или творчества К. Юнга.
В целом можно констатировать, что современная эпоха общесистемного кризиса техногенно-потребительского менталитета и становления нового, антропокосмического мировоззрения, связанного с особым интересом к конструктивным возможностям человеческого сознания и с развертыванием диалога между различными формами постижения бытия, заставляет по-новому взглянуть и на проблему критериев истины.
Критерии истины– то, что удостоверяет истину и позволяет отличить ее от заблуждения.
1. соответствие законам логики;
2. соответствие ранее открытым законам науки;