Как на отрезке отметить точки
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
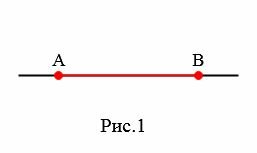 |
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
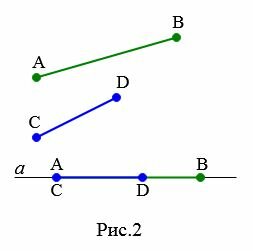 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
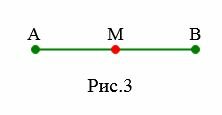 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
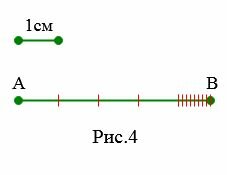 |
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
О числе точек в отрезке
Для просмотра формул ваш браузер должен поддерживать MathML.
| Объявления | Последний пост | |
|---|---|---|
 | Преподаватель мехмата МГУ удостоен международной премии по математике Presburger Award | 28.07.2020 01:04 |
 | Актуарий в PPF Life Insurance (Junior) | 25.03.2021 21:35 |
 | МГУ и Яндекс объявили об открытии на мехмате специализации по анализу данных и машинному обучению | 24.08.2021 00:17 |
Выпишем из Википедии ряд основных понятий математики и проанализируем их на предмет
соответствия друг другу.
Точка — одно из фундаментальных понятий математики, абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект). Для наглядности ограничимся евклидовой геометрией.В евклидовой геометрии точка — это неопределяемое понятие, на котором строится геометрия, то есть точка не может быть определена в терминах ранее определённых объектов. Иными словами, точка определяется только некоторыми свойствами, называемыми аксиомами, которым она должна удовлетворять. В частности, геометрические точки не имеют никакой длины, площади, объёма или какой-либо другой размерной характеристики. Распространённым толкованием является то, что понятие точки предназначено для обозначения понятия уникального
местоположения в евклидовом пространстве.
Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок обычно обозначается [a,b]. Число b- a называется длиной числового отрезка [a,b].
Вырожденными называют математические объекты, обладающие принципиально более простой структурой и смыслом по сравнению с остальными объектами в своём классе, то есть такие, которые, даже будучи взятыми вместе, не дают полного представления о всём классе.
Множество — одно из ключевых понятий математики; это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством.
Если концы отрезка совпадают (a=b), то говорят о вырождении отрезка в точку. Такой вырожденный отрезок нельзя причислить к множеству отрезков, поскольку он не обладает общим для всех отрезков характеристическим свойством – длиной (обладает нулевой длиной).
В связи с вышесказанным заметим, что отрезок не может состоять из отрезков нулевой длины, поскольку операция деления на ноль в математике запрещена. То есть отрезок не может быть составлен из точек. Нельзя говорить о том, что отрезок – множество точек. Правильным ответом на вопрос о числе точек в отрезке будет не множество мощности континуум, а нуль. Ни в отрезке, ни в прямой точек, как составных частей (элементов множества), нет.
Составление из нульмерных объектов объекты, имеющие размерность, можно назвать актом Творения, так как размерность выбирается произвольно. Это могли бы быть и метры, и секунды, и килограммы. В связи с чем можно было бы задавать вопросы типа: сколько (множество какой мощности) секунд в килограмме?
Таким образом, отрезок не может являться примером актуальной бесконечности, а утверждение о существовании множеств с мощностью больше мощности счётного множества ничем не подтверждено.
1
Редактировалось 1 раз(а). Последний 19.07.2021 01:16.
Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 9
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.





































