Как на рисунках изображается вектор
Векторы
Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.
Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.
Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть 
(читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,
В контексте векторов мы применяем = чтобы обозначить их равность.
Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.
Пример 1 Векторы u,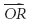 
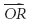
, w показаны на рисунке внизу. Докажите, что u = = w.
Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.
В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.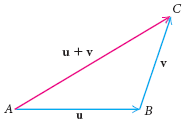
Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = 
, тогда
u + v = + = 
Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.
Если две силы F1 и F2 действуют на один объект, результирующая сила есть сумма F1 + F2 этих двух отдельных сил.
Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.
Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.
Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.
Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.
Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.
Из 
ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Вектор. Виды векторов.
Вектор — в самом элементарном случае это математический объект, который характеризуется
величиной и направлением.
В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая
из его граничных точек является началом, а какая — концом.
У вектора есть длина и определенное направление. Графически вектора изображаются как
направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.
Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.
Как видно на рисунке, начало отрезка – это точка А, концом отрезка является
точка В, а непосредственно вектор обозначен через 
. У направления
вектора существенное значение, если переместить стрелку на другую
сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора
удобно сравнивать с движением физического тела: подумайте, ехать на
рыбалку и с рыбалки – разница огромная.
Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть
разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.
Виды векторов.
Единичным называется вектор, длина которого равна 1.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.
У такого вектора конец и начало совпадают.
Нулевой вектор обычно обозначается как 
. Длина нулевого вектора, или его модуль равен нулю.
Коллинеарные вектора – вектора, которые параллельны одной прямой
или которые лежат на одной прямой.
Сонаправленные вектора. Два коллинеарных вектора a и b называются
сонаправленными векторами только тогда, когда их направления
соответствуют друг другу: a↑↑b
Противоположно направленные вектора – два коллинеарных вектора
a и b называются противоположно направленными векторами, только
когда они направлены в разные стороны: a↑↓b.
Компланарные вектора – это те вектора, которые параллельны одной
плоскости или те, которые лежат на общей плоскости.
В любое мгновение существует плоскость одновременно параллельную
двум любым векторам, поэтому два произвольных вектора являются
Равные вектора. Вектора a и b будут равными, если они будут лежать на
одной либо параллельных прямых и их направления и длины одинаковые.
То есть, такой вектор можно перенести параллельно ему в каждое место
Таким образом, два вектора равны, если они коллинеарные, сонаправленые
и имеют одинаковые длины:
Для координатного представления векторов огромное значение
оказывает понятие проекции вектора на ось (направленную
прямую).
проекциями точек начала и конца вектора на заданную прямую,
при этом проекции добавляется знак “+”, но когда направление
проекции соответственно направлению оси, иначе — знак “–”.
Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция
вектора на ось, которая перпендикулярна ему = 0.
Когда работают с векторами, зачастую вводят так называемую
декартову систему координат и уже в этой системе находят
координаты вектора по базисным векторам.
Разложение по базису геометрически можно показать проекцией
вектора на координатные оси. Когда известны координаты начала и
конца вектора, то координаты данного вектора получают вычитая
из координат конца вектора координат начала вектора.
За базис зачастую выбираются координатные орты, которые обозначаются как 
, соответственно
осям x, y, z. Исходя из этого, вектор 
можно записать в таком виде:
Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование
из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,
кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только
те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).
40 туториалов для создания векторных иллюстраций
В посте собрана подборка обучающих уроков по созданию векторной графики. На мой взгляд большинство материалов покажутся интересными для новичков только начинающих постигать векторное искусство. Но думаю, что специалисты также смогут найти для себя полезные уроки.
Туториалы бесплатные, но почти все на английском языке. Для удобства они поделены на три категории: приступая к работе, создание лиц, дизайн персонажей, ландшафт и окружающая среда и особые эффекты.
Приступая к работе
В этом уроке объясняется, каким образом создавать векторные иллюстрации используя Adobe Illustrator. Приводится объяснение ключевых параметров и инструментов, которое дополняется советами экспертов.
В этом многогранном туториале Вы узнаете основные термины, рассмотрите рабочие процессы и техники, которые помогут начать работать с векторной графикой.
Инструмент «перо» — один из основных в арсенале программы, он особенно важен для начального овладения векторной графикой. Это подробное руководство ставит своей целью познакомить Вас с особенностями и методами работы с незаменимым инструментом компании Adobe. А также с наиболее рациональными способами его использования.
Данный видео-туториал является действительно ценным ресурсом, который объясняет как создавать векторную графику в Illustrator и какую роль в этом процессе играет рисование.
От использования точек кривой Безье до обводки, заливки и придания векторной графике более естественного вида — это лишь некоторые секреты Illustrator из урока, которые существенно пополнят арсенал новичка.
Узнайте, как создавать простые органические формы в Illustrator с этим простым для восприятия руководством от Верле Питерс (Veerle Pieters), графического и веб-дизайнера.
7. Добавление текстуры для векторных иллюстраций
Добавление текстуры — это отличный способ сделать Вашу векторную графику более выразительной, подчеркнуть ее перспективу. В этом очень доступном видео эксперт Illustrator Александра Сесилио (Alexandra Cecilio) демонстрирует как это сделать.
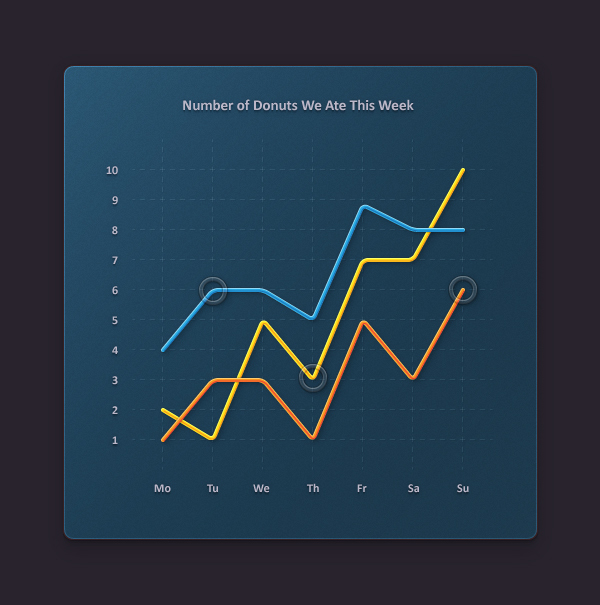
Этот туториал от Андрея Мариуса (Andrei Marius) поможет Вам создать векторный линейный график. Пошагово: начиная с простой сетки до направляющих линий, используя только панель Appearance (один из мощнейших инструментов в Adobe Illustrator) с добавлением некоторых простых фрагментов текста и тонкой штриховки.
Создание лиц
9. Создание векторного глаза
Это очень полезный видео туториал, который показывает процесс создания векторного глаза, а также затемнение кожи.
Это углубленный видео курс, который поможет в овладении искусством создания векторных портретов на основе фотографий.
Еще один замечательный туториал по векторной графике. Руслан Хасанов показывает как манипулировать работой векторных линий и градиентами, чтобы придать работе динамичность.
С возрождением геометрической тенденции, справедливо сказать, что WPAP может быть представлен в большем количестве различных аспектов дизайна. Этот туториал покажет Вам как самостоятельно создать WPAP в Illustrator с помощью мастера WPAP.
Прорисовка волос в векторе может быть довольно мудреной. Этот туториал шаг за шагом показывает как волосы с фотографии превращаются в векторные.
В этом уроке Вы сможете создать иллюстрированный автопортрет в геометрическом стиле. В качестве основы иллюстрации будет использоваться Ваша собственная фотография. Она поможет нарисовать эскиз, а затем завершить оставшуюся часть работы.
Дизайн персонажей
Иллюстратор и дизайнер Юлия Соколова показывает как создать набор портретов, которые идеально подходят для социальных медиа или, к примеру, для обозначения различных категорий и профессий на Вашем сайте.
Джонатан Болл (Jonathan Ball), основатель Poked Studio, обьясняет как с помощью Illustrator основные геометрические фигуры превращаются в уникальных, красочных персонажей.
В этом уроке Вы легко и весело создаете очень простой трафарет, который можно использовать на различных поверхностях (включая футболки, стены, холсты). Сказка Л. Кэррол «Приключения Алисы в Стране чудес» вдохновила автора на создание векторного изображения и написание туториала.
С помощью этого туториала Мэри Винклер (Mary Winkler) собирается показать Вам, как нарисовать чиби персонажа с нуля, используя Shape Builder Tool (Shift-M), Pen Tool (P), прозрачные градиенты, и многое другие инструменты Illustrator.
В руководстве описан процесс создания простого персонажа аниме от начала и до конца.
Узнайте как создаются милые кролики в этом туториале векторной графики. Тренинг использует простые формы и градиенты, которые легко применимы и к иллюстрациям других персонажей.
Этот туториал представляет очень много основных форм для достижения действительно ловкого стиля иллюстраций. А затем «оживляет» йети с помощью палитры холодных цветов.
Здесь Вы сможете увидеть, как создаются персонажи видеоигр. У Вас будет возможность рассмотреть работу с первого эскиза и до самого финала.
Иллюстратор и автор Шейрен Милн (Sharon Milne) показывает, как создать монохромный портрет с фотографии.
Если Вы заядлый любитель футбола, то этот туториал будет особенно кстати. В уроке Сергей Кандаков создает яркую иллюстрацию с эффектом стиля ретро.
Ландшафт и окружающая среда
В этом уроке от векторного художника Андрея Мариуса (Andrei Marius) показано, как можно создать простой дизайн карты в Illustrator.
В этом туториале продемонстрировано, как создать в llustrator эффектный ландшафт окружающей среды. Для выполнения задания будет достаточно базовых знаний об инструментах программы.
Очень простой и последовательный урок от Дианы Тома (Diana Toma), который показывает как нарисовать прекрасные цветы используя градиентные сетки (меш).
Особые эффекты
В этом пошаговом руководстве Вы изучите, как создать «электрический» текст в векторе.
В этом учебном руководстве мы сделаем простой и красивый восточный паттерн в Adobe Illustrator, который будет состоять из различных объектов азиатской культуры.
За прошедшие годы винтажные иллюстрации и ретро-стиль стали вновь популярными в дизайне. В представленном уроке разработчик Бен Стирс (Ben Steers) делится своими методами, которые помогут Вам преобразовать векторные рисунки в ретро-стиль.
С помощью Illustrator можно создавать безупречную векторную графику. Но порой требуются иллюстрации, напоминающие художественные эскизы, выполненные на скорую руку. В уроке показано, как нарисовать векторный рисунок в таком стиле.
Следуя этому туториалу Вы сможете создать эффект блеска в Adobe Illustrator. В основе иллюстрации заложены три эффекта: бумага для заметок, витраж и рваные края. С помощью быстрой трассировки они превращаются в блестящую векторную текстуру.
Полутон — способ воспроизведения монохромного изображения. Он базируется на специфике восприятия картины человеческим глазом для которого область изображения, заполненная крупными точками, ассоциируется с более темными тонами. И наоборот, область, заполненная точками меньшего размера, воспринимается как более светлая. Художник Крис Маквей (Chris McVeigh) покажет, как создать векторный полутон.
В этом учебном руководстве Вы изучите, как создать графический логотип Бэтмена, используя простые формы в Adobe Illustrator. Используются простые инструменты, вроде Ellipse Tool (L) и Shape Builder Tool (Shift + M).
36. Конвертируйте растровое изображение в векторное
Это учебное руководство Inkscape демонстрирует, как преобразовать растровое изображение в векторное при помощи функции Trace Bitmap.
Слайдер — популярный элемент веб-дизайна. В данном туториале показан вариант создания слайдера в векторе.
Сиара Фелен (Ciara Phelan) продемонстрирует Вам как с помощью комбинирования векторных изображений и фотографий можно создать удивительный коллаж.
В этом туториале от одной дизайнерской студии рассказывается как просто нарисовать и трассировать фотографию. Для создания реалистичной иллюстрации в примере используется простая градиентная заливка.
В этом учебном руководстве показано, как создать эффект вышивки крестиком в Adobe Illustrator. Для этого будет использоваться панель Appearance и образцы.