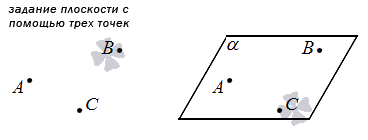Как назвать плоскость тремя буквами
Плоскость
Понятие плоскости
поверхность школьной доски:
Эти поверхности ограничены, у них есть края. Но представление о плоскости мы имеем с их помощью.
Только плоскость простирается безгранично (в любом направлении, заданном на этой плоскости).
Понятие плоскость принадлежит к числу основных понятий геометрии.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
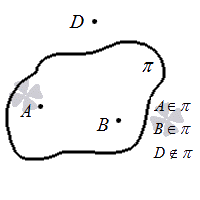
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Определение плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. ( то есть, любая прямая, соединяющая две ее точки, целиком принадлежит ей).
Поделись с друзьями в социальных сетях:
Плоскость в пространстве – необходимые сведения.
В планиметрии плоскость является одной из основных фигур, поэтому, очень важно иметь ясное представление о ней. Эта статья создана с целью раскрытия этой темы. Сначала дано понятие плоскости, ее графическое представление и показаны обозначения плоскостей. Далее плоскость рассматривается вместе с точкой, прямой или другой плоскостью, при этом возникают варианты из взаимного расположения в пространстве. Во втором и третьем и четвертом пункте статьи как раз разобраны все варианты взаимного расположения двух плоскостей, прямой и плоскости, а также точки и плоскости, приведены основные аксиомы и графические иллюстрации. В заключении даны основные способы задания плоскости в пространстве.
Навигация по странице.
Плоскость – основные понятия, обозначения и изображение.
Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости. Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.
При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.
Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.
Взаимное расположение плоскости и точки.
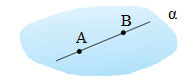
Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.
Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «
К примеру, если точка А не лежит в плоскости 

Прямая и плоскость в пространстве.
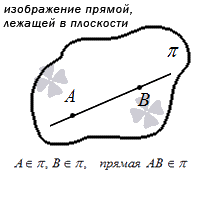
Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «


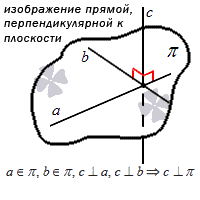
Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «
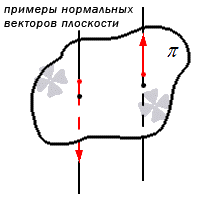
Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости. Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.
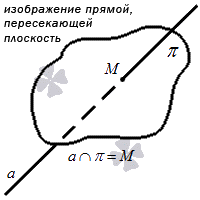
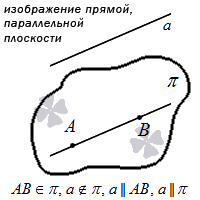
В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «


Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.
Взаимное расположение плоскостей.
Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.
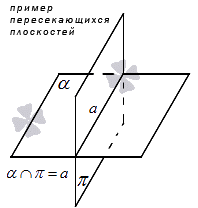
Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В этом случае возникает понятие угла между пересекающимися плоскостями. Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей.
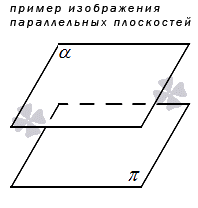
Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей, чтобы получить полное представление об этом варианте взаимного расположения плоскостей.
Также интересны случаи, когда несколько плоскостей пересекаются по одной прямой и несколько плоскостей пересекаются в одной точке. О таком взаимном расположении плоскостей смотрите статьи пучок плоскостей и связка плоскостей.
Способы задания плоскости.
Сейчас мы перечислим основные способы задания конкретной плоскости в пространстве.
Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость с помощью указания координат трех ее различных точек, не лежащих на одной прямой, то мы можем написать уравнение плоскости, проходящей через три заданные точки.
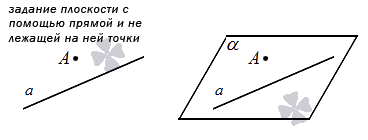
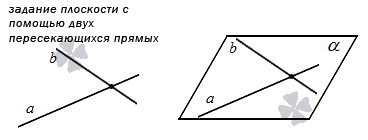
Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки:
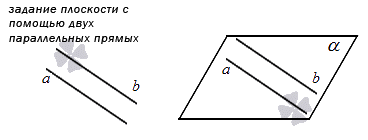
Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых. Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат.
Если в трехмерном пространстве относительно прямоугольной системы координат задана плоскость указанным способом, то мы можем составить уравнение плоскости, проходящей через две параллельные прямые.
Признак параллельности двух плоскостей дает нам еще один способ задания плоскости. Вспомним формулировку этого признака: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны. Следовательно, мы можем задать конкретную плоскость, если укажем точку, через которую она проходит и плоскость, которой она параллельна.
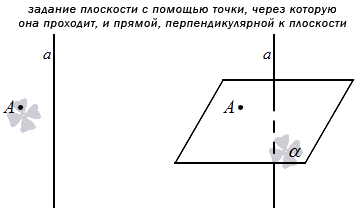
В курсе средней школы на уроках геометрии доказывается следующая теорема: через фиксированную точку пространства проходит единственная плоскость, перпендикулярная к данной прямой. Таким образом, мы можем задать плоскость, если укажем точку, через которую она проходит, и прямую, перпендикулярную к ней.
Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость указанным способом, то можно составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
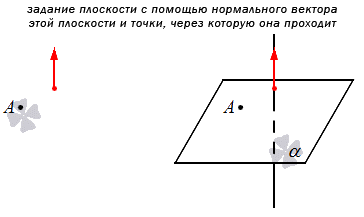
Вместо прямой, перпендикулярной к плоскости, можно указать один из нормальных векторов этой плоскости. В этом случае есть возможность написать общее уравнение плоскости.
На этом завершаем обзор основных способов, с помощью которых определяется конкретная плоскость пространства.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 22
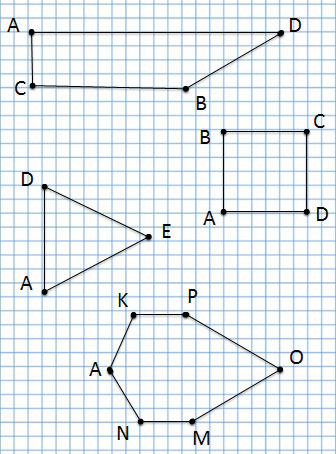
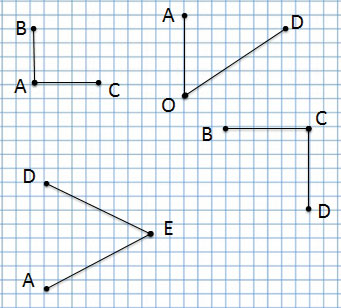
Обозначение геометрических фигур буквами
В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.
Точка
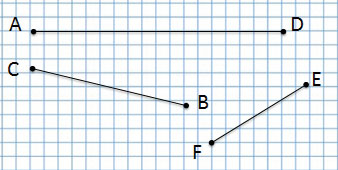
точка А, точка С, точка D, точка Е и точка F.
Отрезок
отрезок AD, отрезок СВ, отрезок FE
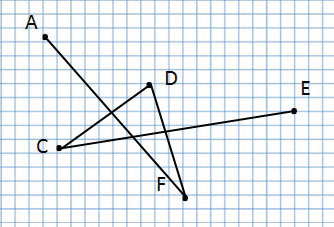
Сколько всего отрезков на данном чертеже?
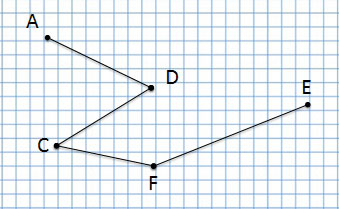
Ломаная линия
А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:
Ломаная линия ACDFE
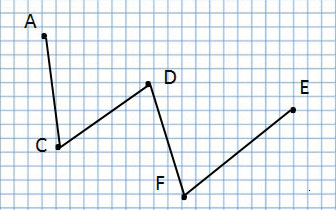
Прочитаю название следующей ломаной линии:
Ломаная линия AFDCE
Многоугольники
Угол
Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.
1 угол: угол BAC или CAB с вершиной А
2 угол: угол AOD или DOA с вершиной О
3 угол: угол AED или DEA с вершиной Е
4 угол: угол BCD или DCB с вершиной С
Поделись с друзьями в социальных сетях: