Как называется уравнение с модулем
Как называется уравнение с модулем
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Точно так же, как и в предыдущем примере, уравнения с модулем могут возникнуть при решении уравнений другого типа, например, иррациональных.
Вот пример подобной ситуации:
Мы могли бы раскрыть скобки, перенести все в одну сторону, привести подобные и решить обычное квадратное уравнение (например, через дискриминант).
Но здесь удобнее поступить по-другому!
Заметим, что в правой части уравнения – формула сокращённого умножения квадрат суммы:
Тогда уравнение станет таким:
Казалось бы, теперь достаточно просто убрать квадраты слева и справа, и получим линейное уравнение.
Будь предельно осторожным: опять вспоминаем простое правило: \( \sqrt<<
И опять на сцене наш модуль:
Чтобы не теряться в таких случаях, научимся решать уравнения с модулем (все три типа).
Уравнения вида |x| = |a|
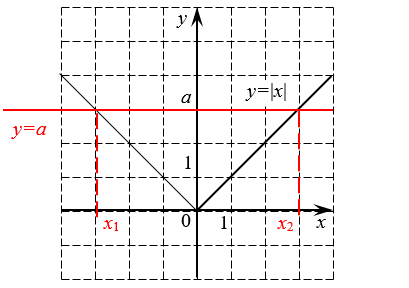
Большинство уравнений с модулем можно решить, используя одно только определение модуля. Например:
Решите уравнение:
Что такое \( \left| x \right|\)?
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Уравнения вида |x| = |y|
Если начнём раскрывать модули по определению, натолкнёмся на множество проверок: какое число больше нуля, какое меньше; в итоге получим большую совокупность, которая затем упростится.
Но можно сделать так, чтобы сразу было всё кратко.
Для этого вспомним свойство модуля №7:
С помощью этого свойства можем избавляться от модулей:
\( \displaystyle \Leftrightarrow \left(
Пример №7
Пример №8
Пример №9
Решения примеров №7-9:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Уравнения вида |x| = y
Отличие от первого типа уравнений в том, что в правой части тоже переменная.
А она может быть как положительной, так и отрицательной.
Поэтому в её неотрицательности нужно специально убедиться, ведь модуль не может равняться отрицательному числу (свойство №1):
\( \left| x \right|=y\text< >\Leftrightarrow \text< >\left\< \begin
Пример №10
Пример №11
Пример №12
Пример 13
Решения примеров №10 — 13
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Метод интервалов в задачах с модулем
Иногда в задачах с модулем, если решать их в лоб, приходится рассматривать очень много вариантов.
Например, если модулей не два, а три, то получится целых 8 уравнений!
Использовать метод интервалов.
Пример №14
Решение:
Рассмотрим первый модуль \(\displaystyle\left| x+3 \right|\). По определению он раскрывается «с плюсом» (то есть выражение под модулем не меняется), если \(\displaystyle x+3\ge 0\), и «с минусом» (то есть все знаки меняются на противоположные), если \(\displaystyle x+3
Аналогично и со вторым:
Проблема только в том, что теперь нам нужно рассмотреть очень много вариантов: по \(\displaystyle2\) варианта для каждого модуля, итого четыре разных, но похожих друг на друга, уравнения.
Если модулей будет не два, а три, получится уже \(\displaystyle8\) уравнений!
Можно ли как-то сократить количество вариантов?
Да, можно – ведь не все условия могут выполняться одновременно: \(\displaystyle x+3
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Проверим полученные корни:
I. \(\displaystyle x=5:\text< >\left| 5+3 \right|-\left| 2\cdot 5-1 \right|=8-9=-1\ne 1\) (корень и правда сторонний).
III. \(\displaystyle x=3:\text< >\left| 3+3 \right|-\left| 2\cdot 3-1 \right|=6-5=1\).
Ответ: \(\displaystyle-\frac<1><3>;\text< >3.\)
Пример 15
Пример №16
\(\displaystyle\left| 3
Решения примеров №15-16:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Модуль в модуле
В некоторых уравнениях встречается «вложенный» модуль, то есть модуль какого-то выражения является частью подмодульного выражения, например:
\(\displaystyle\left| \left| x \right|-5 \right|=3\)
Что делать в таком случае? Все банально: раскрывать модули. Но раскрывать их нужно по очереди. Какой будем раскрывать первым?
А это зависит от того, каким методом ты хочешь решить это уравнение. Рассмотрим два возможных варианта:
I. Данное уравнение является уравнением вида \(\displaystyle\left| f\left( x \right) \right|=a\)
В этом случае первый способ решения будет стандартным для такого типа:
Получили два элементарных уравнения такого же типа, то есть:
Эти четыре числа и будут ответом, можешь проверить их подстановкой в исходное уравнение.
II. Есть ещё один, более универсальный способ, который подойдёт для любых задач, не попадающих ни в какой из стандартных типов.
Метод интервалов.
В этом случае нужно раскрывать модули начиная с самых «глубоких», то есть «внутренних». В нашем случае внутренним будет модуль, выделенный красным цветом:
\(\displaystyle\left| \left| x \right|-5 \right|=3\)
Решение уравнений. Модули 2. Урок 2 из 5
Математика — модули, уравнения с модулями, модули в модулях — никто не умеет их решать, а вы научитесь!
На прошлом уроке мы разобрали с вами базовые уравнения с модулем, а теперь пришло время для настоящей жести.
Модули квадратных трёхчленов, суммы нескольких модулей, модули в модулях. Нас ждут продвинутые задачи и продвинутые методы решений.
Все это — в этом коротком вебинаре!
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Твой ход!
Теперь ты знаешь все о модуле! Я уверен, что ты справишься с любой задачей! И я очень горжусь тобой.
Это было не так сложно, правда? Особенно, когда разбираешь все подробно и поэтапно.
А сейчас мы хотим услышать тебя! Как тебе статья? Понравился разбор понятия модуля? 🙂
Напиши в комментариях свое мнение об этой статье!
Мы читаем все. И ответим на любые твои вопросы.
Добавить комментарий Отменить ответ
5 комментариев
Пока все нормально! Понравилось!
Отлично, Тамара! Заходите еще 🙂
Некоторые комментарии к этой статье:
Марк
14 декабря 2017
Спасибо огромное, повторил, сдал на отлично, Алексею нобелевскую по математике)
Александр (админ)
15 декабря 2017
Марк, наши поздравления с отличной сдачей. Премию Алексею передам 🙂
владимир
19 апреля 2018
нобелевские по математике не присуждаются …
Александр (админ)
19 апреля 2018
Наградим поощрительной грамотой )
Александр (админ)
26 февраля 2019
Gern geschehen, Dascha! Bitte… International Mathematical Unterstützung zu Ihren Diensten ))
Лера
19 мая 2019
Очень хорошо разобрано и объяснено. И за советы спасибо)
Напишите, пожалуйста, автора данной статьи.
Это Алексей Шевчук. Всего было три основных автора и несколько помощников. Алексей писал основную часть в этой статье.
Как решать уравнения с модулем: основные правила
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
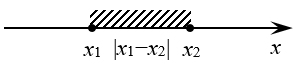
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
\[\left| f\left( x \right) \right|=a\]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]
\[2x+1=5\Rightarrow 2x=4\Rightarrow x=2\]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
\[2x+1=-5\Rightarrow 2x=-6\Rightarrow x=-3\]
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
\[\left| f\left( x \right) \right|=a\Rightarrow f\left( x \right)=\pm a\]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
Опять раскрываем модуль с плюсом и минусом:
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
\[\left| f\left( x \right) \right|=g\left( x \right)\Rightarrow \left\< \begin
Применительно к нашему уравнению получим:
\[\left| 3x-2 \right|=2x\Rightarrow \left\< \begin
Поэтому решим-ка само уравнение:
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
\[\left| f\left( x \right) \right|=g\left( x \right)\]
И решается оно точно так же:
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\Rightarrow f\left( x \right)=\pm g\left( x \right)\]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\]
Элементарно, Ватсон! Раскрываем модули:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left( 2x-7 \right)\]
Рассмотрим отдельно каждый случай:
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
\[2x+3=-2x+7\Rightarrow 4x=4\Rightarrow x=1\]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
\[\left| x-1 \right|=\left| <
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
\[\left[ \begin
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
\[x-<
\[<
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
\[3x-5 \gt 0\Rightarrow \left| 3x-5 \right|=3x-5\]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
\[3x-5=5-3x\Rightarrow 6x=10\Rightarrow x=\frac<5><3>\]
\[x=\frac<5><3>\Rightarrow 3x-5=3\cdot \frac<5><3>-5=5-5=0\]
\[3x-5 \lt 0\Rightarrow \left| 3x-5 \right|=5-3x\]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
\[3x-5 \lt 0\Rightarrow 3x \lt 5\Rightarrow x \lt \frac<5><3>\]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
\[3x-5=0\Rightarrow \left| 3x-5 \right|=0\]
\[0=3x-5\Rightarrow 3x=5\Rightarrow x=\frac<5><3>\]
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
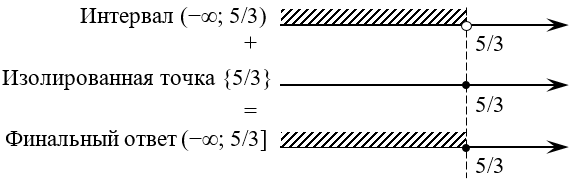
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

Ну и какие тут интервалы? Понятно, что их три:
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Уравнения с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Переменная как под модулем, так и вне модуля
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Первый случай: x ≥ 3. Снимаем модуль:
Значит, больше трёх и потому является корнем исходного уравнения
Ответ:
Квадратные уравнения с заменой |x| = t
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Модуль в модуле
Начинаем с раскрытия внутреннего модуля.
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.



