Как называются алгоритмы содержащие ветвления
Как называются алгоритмы содержащие ветвления
Во многих случаях требуется, чтобы при одних условиях выполнялась одна последовательность действий, а при других – другая.
Если пошел дождь, то надо открыть зонт.
Если прозвенел будильник, то надо вставать.
Если встречу Сашу, то скажу ему …
Если встречу Сашу, то скажу ему …, иначе зайду к нему сам.

Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено и «нет» — условие не выполнено.
Логические выражения. Логический тип данных. Условный оператор
Урок 6. Основы алгоритмизации и программирования на языке Python
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Логические выражения. Логический тип данных. Условный оператор»
· Логический тип данных.
Линейный алгоритм представляет собой простую и предсказуемую последовательность действий, которые не зависят ни от каких факторов. Однако в повседневной жизни мы не всегда можем однозначно предсказать последовательность действий чего-либо, потому как они зависят от некоторых условий. Например, вы решили пойти на улицу и думаете, что надеть. Ваш выбор одежды будет зависеть от того, какая погода на улице. Можно привести и массу других примеров.
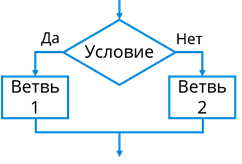
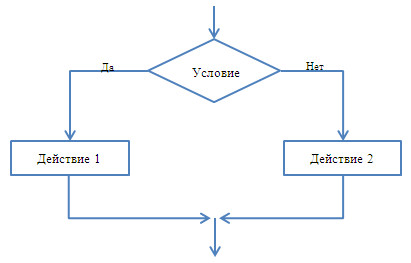
Когда выполняемые действия зависят от некоторых условий, для их записи используются разветвляющиеся алгоритмы. Разветвляющимися называются алгоритмы, содержащие ветвления. Что же такое ветвление? Ветвление – это алгоритмическая конструкция, в которой, в зависимости от некоторого условия, происходит исполнение одной из двух последовательностей действий, которые называются ветвями. Рассмотрим блок-схему ветвления. В верхнем блоке записывается условие. Если условие выполняется, то выполняется одна последовательность команд, в противном случае – другая.
Рассмотрим условие ветвления. В качестве условий в ветвлениях используются логические высказывания. Логическим высказыванием называется утверждение, которое однозначно можно определить как истинное или ложное. Рассмотрим пример. Утверждения о том, что снег белый, в Африке всегда холодно, а человек – хищник, являются логическими высказываниями, так как их правдивость можно легко проверить. А вот вопрос о том, какая сейчас погода, или предложение проверить, не идёт ли на улице дождь, не являются логическими высказываниями, так как вопросы и предложения не являются утверждениями.
Логические значения «истина» и «ложь» могут быть неявно преобразованы к числовым значениям единица и ноль соответственно. В доказательство запишем выражение «False + 3». Как видим, результат этого выражения – 3. Запишем выражение: «True + 2». Результат этого выражения – 3.
При использовании операций сравнения важно помнить о соответствии типов операндов. Так можно сравнить между собой две символьные строки или два числа, но при попытке сравнить между собой символьную строку и число программа вернёт сообщение об ошибке. Однако, так как логические выражения могут быть неявно преобразованы к числовым, то их можно сравнивать с числами.
Решим задачу. Написать модуль для определения истинности утверждения о том, что введённое число является положительным.
Начнём написание модуля. Сначала с помощью инструкции print выведем на экран сообщение о том, что это программа, определяющая истинность утверждения о том, что введённое число –положительное и запрос на ввод числа. Дальше считаем число, введённое пользователем в переменную a. Так как в условии задачи не сказано, что число целое, то при считывании будем преобразовывать значение в вещественный тип float. Дальше с помощью инструкции print выведем на экран истинность утверждения «a > 0».
Рассмотрим алгоритмы, в которых последовательность действий изменяется в зависимости от входных данных. Для записи таких алгоритмов в языке Python используется инструкция ветвления. Эта инструкция является составной, то есть она содержит в себе другие инструкции. Рассмотрим её запись. Она начинается со служебного слова if, после которого, через пробел, следует условие ветвления. Условием ветвления является выражение логического типа. Дальше следует двоеточие, после которого, начиная со следующей строки с отступом, записываются инструкции, которые будут выполняться в том случае, если условие ветвления будет возвращать значение «истина». Далее на одном уровне со словом if следует служебное слово else, после которого записывается двоеточие. Со следующей строки с отступом записываются инструкции, которые будут выполняться в случае, если условие ветвления вернёт значение «ложь». Служебные слова if и else переводятся на русский язык, как «если» и «иначе» соответственно. В языке Python, при записи инструкции ветвления, важно соблюдать отступы, иначе программа не будет работать.
Приведём пример инструкции ветвления. Предположим, что нам нужно присвоить переменной M наибольшее из значений, содержащихся в переменных a и b, или любое из значений, если они равны. Для того, чтобы это сделать, запишем инструкцию ветвления с условием: a > b. Если это условие будет выполняться, то мы присвоим переменной M значение переменной a. Если же это условие не будет выполняться, то мы присвоим переменной M значение переменной b.
Приведённая запись инструкции ветвления называется её полной формой, но описанную задачу можно решить иначе. Для этого можно до инструкции ветвления присвоить переменной M значение переменной b. Тогда нам не нужна часть инструкции ветвления, начиная со служебного слова else. Её можно не записывать. Тогда в случае, если условие ветвления выполняется, будет выполнена инструкция, которая следует после условия, в противном случае выполнение инструкции ветвления будет завершено. Такая запись инструкции ветвления называется её сокращённой формой.
Решим задачу с использованием ветвлений. Треугольник на координатной плоскости задан целочисленными координатами своих вершин, не лежащих на одной прямой. Определить, является ли заданный треугольник прямоугольным.
Для решения задачи мы вычислим расстояния между вершинами треугольника. Таким образом, мы определим длины его сторон. Согласно теореме Пифагора, в прямоугольном треугольнике сумма квадратов длин двух наименьших сторон равна квадрату длины наибольшей стороны. Обратим внимание, что для проверки того, является ли треугольник прямоугольным, нам необязательно знать длины его сторон. Достаточно знать их квадраты. Таким образом в начале мы можем вычислять не расстояния между вершинами треугольника, а их квадраты. Это позволит избежать лишних вычислений.
Напишем модуль для решения задачи. С помощью инструкции print выведем на экран сообщение о том, что это программа, определяющая является ли треугольник прямоугольным. При помощи ещё одной инструкции print выведем на экран запрос на ввод координат первой вершины треугольника. Дальше запишем инструкцию считывания значений переменных x1 и y1. Так как по условию задачи координаты вершин целочисленные, то при считывании мы будем преобразовывать их значения в целочисленный тип int. Теперь дважды скопируем последние две инструкции и изменим их для ввода координат второй и третьей вершин треугольника соответственно. После того, как мы считали координаты вершин треугольника, определим квадраты длин его сторон. Для этого присвоим переменным kv_a, kv_b и kv_c соответственно квадраты расстояний между вершинами 1 и 2, 2 и 3, а также 3 и 1. Для того, чтобы определить является ли треугольник прямоугольным, нам нужно определить, какая из его сторон является наибольшей. Условимся, что наибольшей будет сторона c. Чтобы наибольшей стала сторона c, запишем две инструкции ветвления. В первой инструкции, если значение переменной kv_a больше значения kv_c, то мы поменяем их местами. Во втором ветвлении, если kv_b больше kv_c, то мы поменяем их значения местами. Теперь запишем инструкцию ветвления, определяющую, является ли треугольник прямоугольным. Его условием будет то, что сумма значений kv_a и kv_b равна значению kv_c. Если это так, то с помощью инструкции print выведем на экран сообщение о том, что заданный треугольник является прямоугольным. В противном случае мы с помощью инструкции print выведем на экран сообщение о том, что заданный треугольник не является прямоугольным.
print (‘Программа, определяющая, является ли треугольник прямоугольным.’)
print (‘Введите координаты первой вершины треугольника.’)
x1, y1 = int (input ()), int (input ())
print (‘Введите координаты второй вершины треугольника.’)
x2, y2 = int (input ()), int (input ())
print (‘Введите координаты третьей вершины треугольника.’)
x3, y3 = int (input ()), int (input ())
kv_a, kv_c = kv_c, kv_a
kv_b, kv_c = kv_c, kv_b
if kv_a + kv_b == kv_c:
print (‘Заданный треугольник является прямоугольным.’)
print (‘Заданный треугольник не является прямоугольным.’)
Сохраним описанный модуль и запустим его на выполнение. Зададим вершины треугольника в точках: (1; 7), (7; 7) и (1; 1). Как видно на рисунке, данный треугольник является прямоугольным. Программа вывела на экран сообщение об этом. Снова запустим модуль на выполнение и зададим вершины треугольника в точках: (1; 7), (7; 4) и (13; 1). Очевидно, что заданный треугольник не является прямоугольным. Программа вывела сообщение об этом. Программа работает правильно. Задача решена.
· Разветвляющимися называются алгоритмы, которые содержат конструкции ветвления.
· Ветвление – это алгоритмическая конструкция, в которой, в зависимости от некоторого условия, происходит исполнение одной из двух последовательностей действий, которые называются ветвями.
· Условиями ветвлений являются логические высказывания – утверждения, истинность которых можно определить однозначно.
· Для хранения данных об истинности логических высказываний в языке Python используются переменные логического типа bool. Они могут принимать одно из двух значений: True или False.
· Для записи ветвлений в языке Python используется соответствующая инструкция, у которой есть полная и сокращённая формы.
Алгоритмические конструкции
Алгоритм на языке КуМир записывается так:
алг квадрат
сместиться на вектор (0,2)
сместиться на вектор (2,0)
сместиться на вектор (0,-2)
сместиться на вектор (-2,0)
Без этой конструкции или за пределами ее программа не может выполнить алгоритм.
Так же на первой строке нужно указать исполнителя для которого вы пишите алгоритм.
использовать ИМЯ_ИСПОЛНИТЕЛЯ (слово использовать с маленькой буквы, имя исполнителя с заглавной буквы).
Правильные конструкции будут с полужирном начертанием, правильные команды будут выделены синим, название исполнителя должно быть зеленым цветом.
Вспомогательный алгоритм — это фрагмент программного кода (подпрограмма), к которому можно обратиться из любого места основной программы. Эта подпрограмма обычно имеет входные и выходные данные.
Роль вспомогательного алгоритма: упростить работу с большим кодом. Задав имя последовательности команд, можно многократно обращаться к этой последовательности, указывая только ее имя.
алг забор | Основной алгоритм
звено | Обращение к вспомогательному алгоритму
алг звено | Вспомогательный алгоритм
Метод последовательной детализации
Использованный нами подход облегчает программирование сложных задач. Задача разбивается на более простые подзадачи. Решение каждой оформляется в виде вспомогательного алгоритма, а основной алгоритм организует связку между ними.
Метод программирования, при котором сначала пишется основная программа, в ней записываются обращения к пока еще не составленным подпрограммам, а потом описываются эти подпрограммы, называется методом последовательной (пошаговой) детализации. Причем количество шагов детализации может быть гораздо большим, чем в нашем примере, поскольку сами подпрограммы могут содержать внутри себя обращения к другим подпрограммам.
Сборочный метод
Возможен и другой подход к построению сложных программ: первоначально составляется множество подпрограмм, которые могут понадобиться при решении задачи, а затем пишется основная программа, содержащая обращения к ним. Подпрограммы могут быть объединены в библиотеку подпрограмм и сохранены в долговременной памяти компьютера. Такую библиотеку можно постепенно пополнять новыми подпрограммами.
Например, если для управления графическим исполнителем создать библиотеку процедур рисования всех букв и цифр, то программа получения любого текста будет состоять из команд обращения к библиотечным процедурам.
Описанный метод называется сборочным программированием.
Часто в литературе по программированию используется такая терминология: метод последовательной детализации называют программированием сверху вниз, а сборочный метод — программированием снизу вверх.
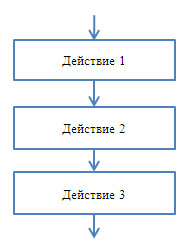
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Графическое представление алгоритмической конструкции «следование» приведено на рисунке справа.
алг закрашивание клетки
Графическое представление и общий вид алгоритмической конструкции «ветвление» приведено на рисунке справа.
Алгоритм ветвления. Отличие от алгоритмов линейной структуры
Статья рассказывает про алгоритмы с разветвлённой структурой. Читатель узнает, чем их решение отличается от решения линейных алгоритмов, как выглядит программный способ записи таких алгоритмов, а также какова будет блок-схема.
В предыдущей статье шла речь об алгоритмах, их особенностях и свойствах. Особое внимание было уделено линейной структуре как самому простому способу реализации. Сегодня поговорим о более сложных алгоритмах, обладающих разветвлённой структурой. Но прежде чем продолжать, следует кое-что вспомнить.
Алгоритм – это ясный перечень действий, который направлен на решение какой-либо задачи. Одно из свойств алгоритма — дискретность. Дискретность связана с наличием в алгоритмической последовательности ряда операций (этапов, действий), выполняемых пошагово, то есть дискретно. Алгоритм обладает свойством дискретности, так как он представляет собой процесс решения задачи в виде последовательного выполнения простых шагов. И каждое действие исполняется лишь после окончания исполнения предыдущего. Также предполагается наличие определённых исходных данных и результата выполнения.
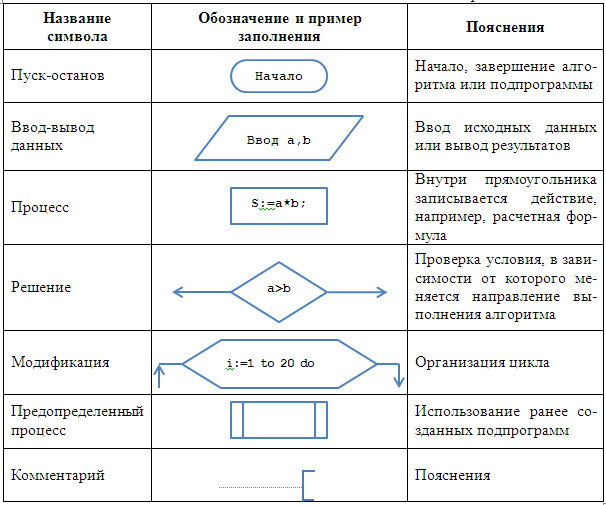
Блок-схема — графический способ описания алгоритмов. Графическое представление обеспечивает наглядность и упрощает запись, делая последовательность более понятной. При использовании схемы каждому действию соответствует определённая геометрическая фигура (эти фигуры называют блоками). Вот наиболее часто употребляемые:
Ещё раз о линейности
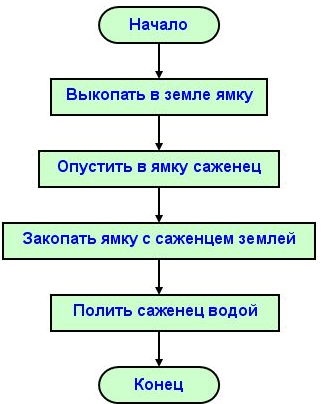
Линейная последовательность — самая простая из возможных структур. При наличии линейности команды выполняются в чёткой последовательности и в порядке их записи, то есть друг за другом. Вот линейная алгоритмическая последовательность посадки дерева: 1) выкапывание ямки в земле; 2) размещение в ямке саженца; 3) закапывание ямки; 4) поливание места посадки водой.
Такой линейный алгоритм имеет следующую блок-схему:
А вот и общая схема линейного алгоритма:
Ветвление в алгоритмических последовательностях
На практике очень редко встречается, чтобы последовательность всех требуемых действий была известна заранее. Если на минуту покинуть мир алгоритмизации и программирования, можно спроецировать ветвление на многие жизненные ситуации. Если на улице дождь, человек берёт зонт, если очень жарко, будет выбрана одежда полегче и т. д. Всё зависит от условия выбора. Как тут не вспомнить рыцаря на распутье из русских народных сказок?
Подобная ситуация заставляет принимать решения с учётом определённого условия. Если нужна жена, то витязь идёт направо, если богатство, то налево, если жизнь не мила, то прямо. Условия, которые влияют на решение, располагаются между словами «если» и «то».
От значения условий зависит дальнейшее поведение. Когда условие выполняется, оно принимает значение «истина», когда нет — «ложь». Иногда анализ ситуации и выбор не вызывают особых затруднений, а иногда принять решение очень трудно. А всё потому, что принимающий решение пытается продумать каждый из вариантов и предугадать последствия выбора. Нельзя не вспомнить гроссмейстера, который анализирует позицию на ходы вперёд, прежде чем передвинуть фигуру на шахматной доске.
Компьютерные программы и игры тоже построены на выборе действий. А блок-схема при наличии ветвления приобретает иной вид:
Логика разветвляющих алгоритмов
Логику можно описать следующим образом:
Ветвление — метод и форма организации действий, когда в зависимости от выполнения определённого условия совершается та либо иная последовательность шагов.
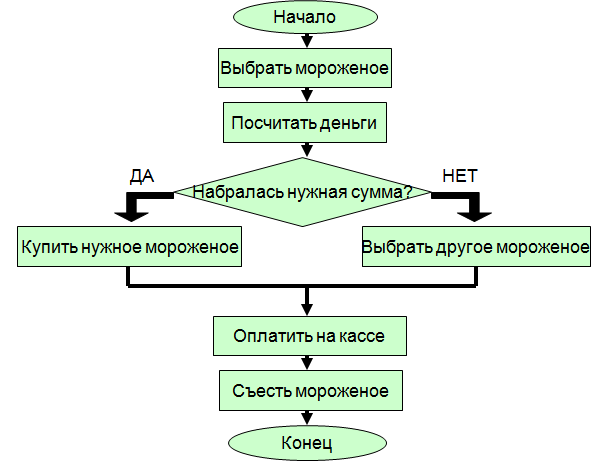
В результате совсем несложно составить алгоритм покупки мороженого с учётом наличия необходимой суммы денег. Описать эту алгоритмическую последовательность с помощью схемы и блоков тоже не составит труда:
Для закрепления можно решить задачу.
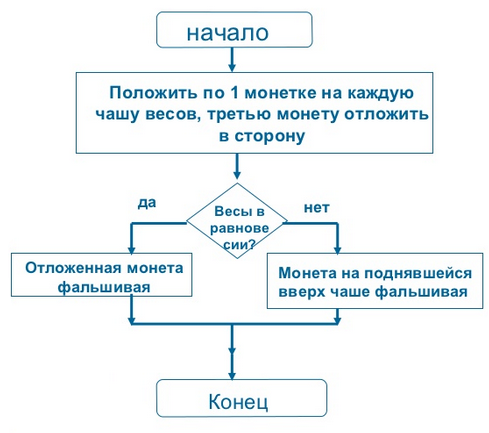
Есть 3 монеты одинакового достоинства. Одна из монет фальшивая (известно, что она имеет меньший вес). Найдите фальшивую монету на чашечных весах без гирь с помощью только одного взвешивания.
Решение легко описывается посредством схематических блоков:
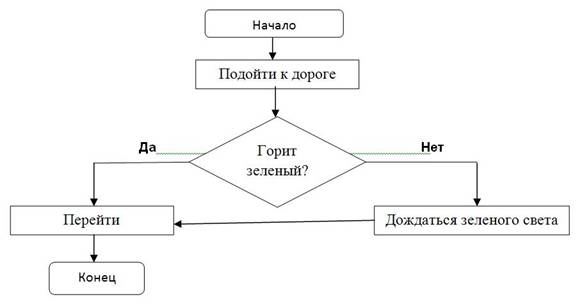
Следующий пример легко экстраполируется в жизнь. Речь идёт об алгоритме для перехода дороги при наличии светофора. Он имеет следующий вид: 1. Подходим к светофору. 2. Смотрим, какой горит свет. 3. Если зелёный, переходим дорогу. 4. Если красный, ждём, пока загорится зелёный, а потом переходим дорогу.
Программный способ записи
Чтобы алгоритм было понятен компьютеру, машине и любой другой цифровой системе, следует оформить его в таком виде, который эта система способна воспринимать. То есть надо написать программу, используя для этого команды из СКИ. СКИ — это список команд исполнителя — перечень команд, ему понятных. А любой исполнитель способен исполнить лишь те команды, которые включены в его СКИ, а если говорить человеческим языком — входят в набор его компетенций.
Для примера можно реализовать алгоритм на языке программирования Pascal. Исходя из вышесказанного, следует использовать команды, входящие в терминологию Pascal.
Простейший пример описания алгоритма с разветвляющейся структурой — условный оператор IF. Полная конструкция этого условного оператора имеет следующий вид:
Здесь if — это «если», then — это «то», else — «иначе».
Условный оператор работает просто: — вычисляется значение логического выражения, которое расположено после служебного слова IF; — если результат — истина, выполняется оператор 1, который размещён после THEN, причём действие после ELSE пропускается; — если результат — ложь, пропускается уже действие после THEN, а действие после ELSE выполняется с помощью оператора 2.
Теперь можно вспомнить пресловутого витязя на распутье и написать простую программу, реализующую этот алгоритм с помощью соответствующих условных операторов.
Попробовать этот алгоритм в работе можно на любом онлайн-компиляторе, поддерживающим Pascal. Но не стоит на этом останавливаться — лучше всего написать собственную программу, что позволит получить максимальную пользу от урока.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 2.4. Основные алгоритмические конструкции
§ 2.4. Основные алгоритмические конструкции
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
Человеку в жизни приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.
Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.
2.4.1. Следование. Основные алгоритмические конструкции
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Графическое представление алгоритмической конструкции «следование» приведено на рис. 2.8.
Пример 1. Линейный алгоритм приготовления отвара шиповника.
Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний.
Пример 2. У исполнителя Робот есть четыре команды перемещения (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение, обозначенное звёздочкой:
Пример 3. Дан фрагмент линейного алгоритма:
Выясним, какое значение получит переменная s после выполнения этого фрагмента алгоритма. Для этого составим таблицу значений переменных, задействованных в алгоритме:
Составленная нами таблица значений переменных моделирует работу исполнителя этого алгоритма.
Пример 4. Некоторый исполнитель может выполнять над целыми ЧЧ0, числами кроме операций сложения, вычитания, умножения и деления ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.
Покажем, как с помощью этих операций можно реализовать алгоритм работы кассира, выдающего покупателю сдачу (s) наименьшим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10)рублей.
Исполните алгоритм для s = 745 и s = 1864. Составьте соответствующие таблицы значений переменных.
Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
2.4.2. Ветвление. Основные алгоритмические конструкции
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Блок-схема ветвления представлена на рис. 2.9. Каждая ветвь может быть любой степени сложности (рис. 2.9, а), а может вообще не содержать предписаний (рис. 2.9, б).
На алгоритмическом языке команда ветвления записывается так:
Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:
А В — А больше В;
А>=В — А больше или равно В;
А<>В — А не равно В.
Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.
Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.
Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.
Пример 8. Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.
Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.
Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, Б и С.
Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:
Пример 10. Алгоритм решения линейного уравнения ах + b = 0.
Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:
| справа свободно слева свободно сверху свободно снизу свободно клетка чистая | справа стена слева стена сверху стена снизу стена клетка закрашена |
Также Робот может действовать в зависимости от выполнения составных условий.
Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.
если справа свободно или снизу свободно
то закрасить
все
если справа стена
то влево
все
если слева стена
то вправо
все
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Алгоритмы с ветвящейся структурой» (217044). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Повторение. Основные алгоритмические конструкции
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.
В зависимости от способа организации повторений различают три типа циклов:
Цикл с заданным условием продолжения работы (цикл-ПОКА, цикл с предусловием)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.10.
На алгоритмическом языке эта конструкция записывается так:
Выполняется цикл-ПОКА следующим образом: 1) проверяется условие (вычисляется значение логического выражения); 2) если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу.
Пример 12. Алгоритм, по которому из всех имеющихся кирпичей отбираются целые кирпичи и складываются в машину.
алг отбор
нач
нц пока есть кирпичи
взять один кирпич
если кирпич целый
то положить кирпич в машину
иначе отложить кирпич в сторону
все
кц кон
Пример 13. Правее Робота (клетка со звёздочкой) расположен коридор неизвестной длины. Необходимо, чтобы Робот закрасил все клетки этого коридора.
Пока будет выполняться условие справа свободно, Роботу следует выполнять команды:
Соответствующий алгоритм для Робота будет иметь вид:
Пример 14. Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления натурального числа х на натуральное число у.
Представим операцию деления как последовательные вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет равно частному от деления q, а последняя разность — остатку от деления r.
Исполним этот алгоритм для х = 23 и у = 5.

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с предусловием» (217033). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.11.
На алгоритмическом языке эта конструкция записывается так:
Выполняется цикл-ДО следующим образом: 1) выполняется тело цикла; 2) проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется («Нет»), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз.
Пример 15. Алгоритм по выучиванию наизусть четверостишия.
алг четверостишие
нач
нц
прочитать четверостишие по книге 1 раз
рассказать четверостишие
кц при не сделал ошибку кон
Пример 16. Вычислим значение переменной b согласно следующему алгоритму:
Составим таблицу значений переменных, задействованных в алгоритме:
Пример 17. Спортсмен приступает к тренировкам по следующему графику: в первый день он должен пробежать 10 км; каждый следующий день следует увеличивать дистанцию на 10% от нормы предыдущего дня. Как только дневная норма достигнет или превысит 25 км, необходимо прекратить её увеличение и далее пробегать ежедневно ровно 25 км. Начиная с какого дня спортсмен будет пробегать 25 км?
Пусть х — количество километров, которое спортсмен пробежит в некоторый i-й день. Тогда в следующий (i + 1)-й день он пробежит х + 0,1х километров (0,1х — это 10% от х).
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с постусловием» (217037). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром)
Логика работы этой конструкции описывается схемой, показанной на рис. 2.12.
На алгоритмическом языке эта конструкция записывается так:
нц для i от i1 до i2 шаг R
кц
В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения il до конечного значения i2 с шагом R.
Выполняется цикл-ДЛЯ следующим образом: 1) параметру цикла присваивается начальное значение; 2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.
Если величина шага в цикле с параметром равна единице, то шаг не указывают. Мы ограничимся рассмотрением именно таких циклов.
В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.
Пример 18. Алгоритм переправы через реку воинского отряда из пяти человек. Солдаты могут воспользоваться помощью двух мальчиков — хозяев небольшой лодки, в которой может переправиться или один солдат, или два мальчика.
алг переправа
нач
нц для i от 1 до 5
два мальчика переправляются на противоположный берег
один мальчик высаживается на берег, другой плывёт обратно
солдат переправляется через реку
мальчик возвращается на исходную позицию
кц
кон
Пример 19. Составим алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а.
При составлении алгоритма воспользуемся единой формулой, в которой число умножений равно показателю степени:
Исполним этот алгоритм для а = 4 и n = 3.
Пример 20. Для исполнителя Робот цикл с известным числом повторений реализуется с помощью следующей конструкции:
Так, если правее Робота не встретится препятствий, то, выполнив приведённый ниже алгоритм, он переместится на пять клеток вправо и закрасит эти клетки:
алг
нач
нц 5 раз
вправо; закрасить
кц
кон
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с параметром» (217024). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Основные алгоритмические конструкции. Самое главное
Для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения.
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными.
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию «повторение», называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла. В зависимости от способа организации повторений различают три типа циклов: