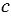Как называются две пересекающиеся прямые

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

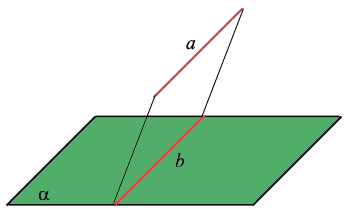
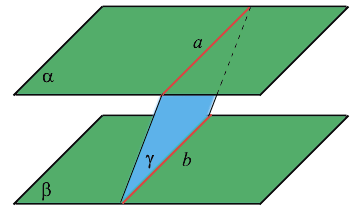
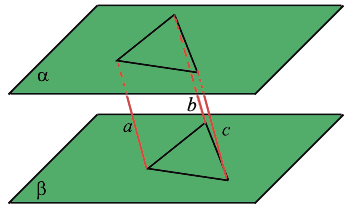
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

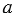
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.

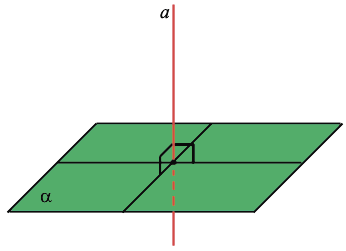
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

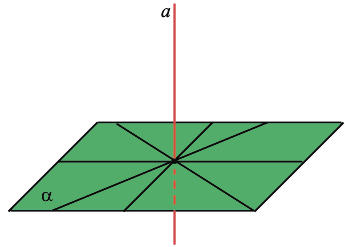
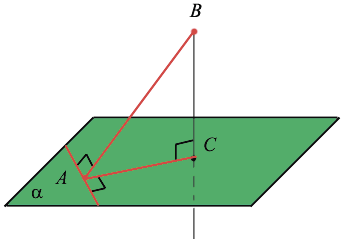
Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

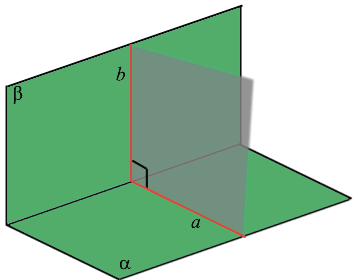
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

3.4. Взаимное положение прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.

Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).

.

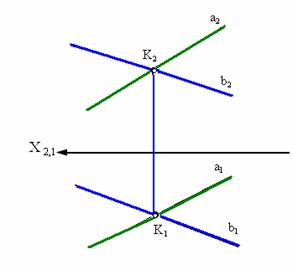
Рис. 3.4. Пересекающиеся прямые

2. Параллельные прямые

На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.

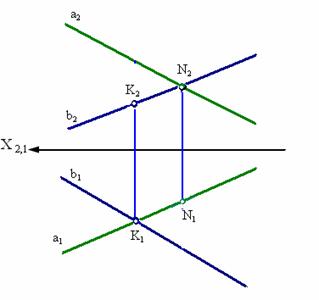
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

.

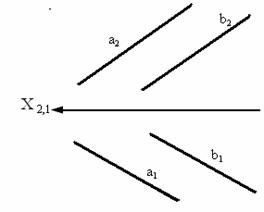
Рис. 3.5. Изображение параллельных прямых

.

Источник

Пересекающиеся прямые

Пересекающиеся прямые — это в евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений.

Содержание:

Понятие пересекающихся прямых

Определение. Если две прямые имеют только одну общую точку, то такие прямые называют пересекающимися.

На рисунке 2.291 прямые пересекаются в точке О.

Можно доказать такую теорему.

Теорема 1. Через две пересекающиеся прямые можно провести плоскость, и только одну.

Несколько прямых могут пересекаться не в одной точке, а, например, попарно. На рисунке 2.292 изображено пересечение трех прямых, каждые две из которых пересекаются только в одной точке. При этом образуется треугольник и вся эта фигура всегда лежит в одной плоскости.

Четыре прямые, каждые две из которых имеют только одну общую точку, образуют четырехугольник (рис. 2.293).

На рисунках 2.294, 2.295 изображены куб и тетраэдр, у которых продолжены их ребра. Мы видим, что в каждой вершине куба и тетраэдра пересекаются три прямые.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Как называются две пересекающиеся прямые

Прямые линии в пространстве могут быть параллельными , пересекающимися и скрещивающимися . Рассмотрим подробнее каждый случай.

1. Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Рисунок 33. Параллельные прямые

Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 3 4 ). В рассмотренном случае проекции отрезков на плоскость П ₃ пересекаются, следовательно, они не параллельны.

Решение этого вопроса можно получить сравнением двух соотношений если:

Рисунок 34. Прямые параллельные профильной плоскости проекций

2. Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 3 5 ).

Рисунок 35. Пересекающиеся прямые

В общем случае справедливо и обратное утверждение, но есть два частных случая:

1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.3 6 ), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.

2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 3 7 ).

О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции ( А ₁В₁ ∩ С ₁D₁ Þ АВ ∩ СD ).

3. Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Источник