Как зашифровать фамилию в rsa

Как зашифровать фамилию в rsa

RSA (Rivest-Shamir-Adleman) является одной из первых криптосистем с открытым ключом и широко используется для безопасной передачи данных. В такой криптосистеме ключ шифрования является открытым и отличается от ключа расшифровки, который хранится в секрете (private). В RSA эта асимметрия основана на практической сложности факторизации произведения двух больших простых чисел, «проблема факторинга». Аббревиатура RSA состоит из начальных букв фамилий Рона Ривеста, Ади Шамира и Леонарда Адлемана, которые впервые публично описали алгоритм в 1978 году. Клиффорд Кокс, английский математик, работающий в Британском разведывательном управлении правительственной связи (GCHQ), разработал эквивалентную систему в 1973 году, но это не было рассекречено до 1997 года.

Пользователь RSA создает и затем публикует открытый ключ на основе двух больших простых чисел вместе с дополнительным значением. Простые числа должны храниться в секрете. Любой может использовать открытый ключ для шифрования сообщения, но с помощью опубликованных в данный момент методов, и если открытый ключ достаточно велик, только тот, кто знает простые числа, может расшифровать сообщение. Нарушение шифрования RSA известно как проблема RSA. Остается открытым вопрос, насколько это сложно, как проблема факторинга.

RSA является относительно медленным алгоритмом, и из-за этого он реже используется для прямого шифрования пользовательских данных. Чаще всего RSA передает зашифрованные общие ключи для шифрования с симметричным ключом, который, в свою очередь, может выполнять массовые операции шифрования-дешифрования на гораздо более высокой скорости.

Источник

RSA: от простых чисел до электронной подписи

Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Содержание

Определения и обозначения

Описание криптосистемы RSA

Асимметричные криптографические системы

Шифрование и дешифрование

Получение подписи сообщения по RSA

Электронная подпись документов

Введение

Наверняка вы сталкивались с таким понятием, как «электронная подпись». Если обратиться к федеральному закону, то можно найти следующее её определение:

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:

Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования

Шифртекст – данные, полученные в результате применения шифра к открытому тексту

Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)

Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.

Факторизация – процесс разложения числа на простые множители.

НОД – наибольший общий делитель.

Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.

Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.

Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.

Как оно устроено

Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают

Асимметричные криптосистемы

Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:

Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть. Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.

В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя «закрыть» на физический замок. Таким образом возникают вопросы: что такое ключ и замок? Как Бобу создать ключи? Каким образом ключи связаны и как с их помощью зашифровать сообщение? Здесь нам поможет математика.

Теперь к математике

Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.

Подобным свойством обладает операция возведения числа в степень по модулю:

Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.

Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.

Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.

Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:

где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:

Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).

Возвращаемся к генерации ключей. Выберем целое число e:

Для него вычислим число d:

Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.

Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.

Шифруем, дешифруем.

Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:

Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:

Здесь нам понадобится теорема Эйлера:

Также полезной будет китайская теорема об остатках:

Получаем подпись сообщения

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:

Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте «зашифруем» m с помощью d:

Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n). По аналогии с расшифрованием, проверка подписи осуществляется возведением подписи s в степень открытой экспоненты e:

Если Алиса получила, что m ≡ m′, то подпись считается правильной.

Дочитавших до этого места хочу поздравить с получением первой цифровой подписи «на бумаге»!

Подпись документов

Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько «мешается». Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.

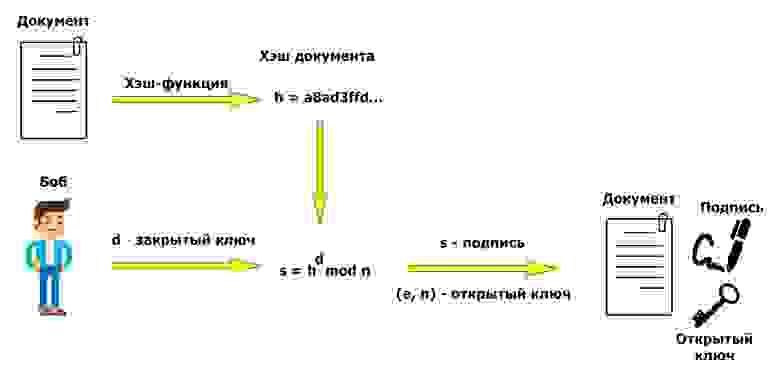
На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:

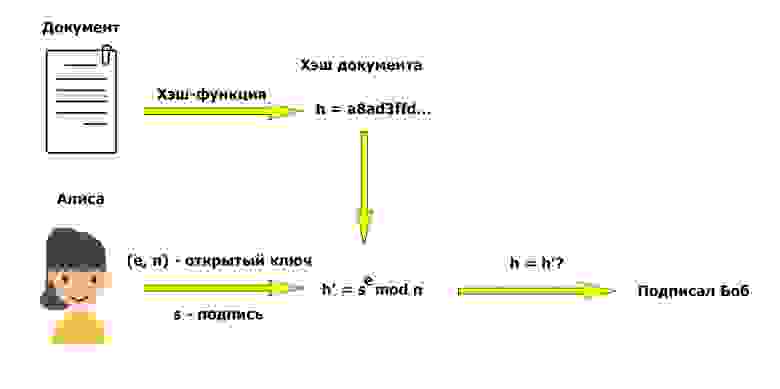
В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.

Заключение

Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.

Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. «Следующей по сложности» я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.

Спасибо за внимание!

Источники

Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone

Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016

Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.

NIST Special Publication 800-57 Part 3 Revision 1

Источник

Хватит использовать RSA

RSA — первый широко используемый алгоритм асимметричной криптографии, который до сих пор популярен в индустрии. Он относительно прост, на первый взгляд. Шифрование и подпись RSA можно посчитать на листке бумаги, чем часто занимаются студенты на лабораторных работах.
Но существует просто огромное количество нюансов, без учёта которых вашу реализацию RSA сможет взломать даже ребёнок.

По какой-то причине люди до сих пор считают RSA хорошим алгоритмом. Но на самом деле, простор для выстрела в ногу при реализации RSA чрезвычайно огромен. Слабые параметры проверить трудно, если не невозможно. А слабая производительность алгоритма побуждает разработчиков использовать рискованные способы её повысить.

Хуже того, атаки типа padding oracle, которые изобрели более 20 лет назад, актуальны и сегодня.
Даже если в теории и возможно имплементировать RSA корректно, на практике такой «подвиг» совершить почти невозможно. И уязвимости, постоянно возникающие уже на протяжении десятилетий, это только подтверждают.

Пару слов об алгоритме RSA

Если знаете, как работает RSA, эту часть можно пропустить.

RSA — криптосистема с открытым ключом, у которой есть два применения.

Первый — шифрование, когда Алиса публикует свой открытый ключ и Боб, зная его, может зашифровать сообщение, которое сможет прочитать только Алиса, расшифровав его своим закрытым ключом.

Второй — цифровая подпись, которая позволяет Алисе подписать сообщение своим закрытым ключом так, чтобы все могли проверить эту подпись с помощью её открытого ключа.

Оба алгоритма отличаются незначительными деталями, поэтому будем их называть просто RSA.

Чтобы начать работать с RSA, Алисе нужно выбрать два простых числа p и q, которые вместе образуют группу чисел по модулю N = pq. Потом Алисе нужно выбрать открытую экспоненту e и секретную d такие, что . По сути, e и d должны быть взаимно просты.

Как только эти параметры будут выбраны, Боб может послать Алисе сообщение M, вычислив . Алиса может затем расшифровать сообщение, вычислив .
Цифровая подпись происходит ровно наоборот. Если Алиса хочет подписать сообщение, она вычисляет подпись , которую Боб может проверить, убедившись, что сообщение

Вот как бы и всё, это основная идея. К Padding oracles мы вернёмся попозже, а пока давайте посмотрим что можно сделать если параметры RSA выбраны неверно.

Начало конца

Для работы RSA требуется выбрать довольно много параметров. К сожалению, невинные на первый взгляд методы их выбора могут навредить безопасности. Давайте пройдемся по каждому из них и посмотрим, какие неприятные сюрпризы вас ждут.

Генерация простых чисел

Безопасность RSA основана на том факте, что имея большое число N, являющееся произведением двух простых чисел p и q, разложение N на простые множители, не зная p и q сделать трудно. Разработчики несут ответственность за выбор простых чисел, составляющих модуль RSA. Этот процесс чрезвычайно медленный по сравнению с генерацией ключей для других криптографических протоколов, где достаточно просто выбрать несколько случайных байтов. Поэтому, вместо того чтобы генерировать действительно случайное простое число, разработчики часто пытаются создавать числа определенной формы. Это почти всегда плохо кончается. Существует много способов выбора простых чисел таким образом, чтобы факторинг N был простым. Например, p и q должны быть глобально уникальными. Если p или q когда-либо повторно используются в других модулях RSA, то оба множителя можно легко вычислить с помощью алгоритма GCD. Плохие генераторы случайных чисел делают этот сценарий довольно вероятным, и исследования показали, что примерно 1% трафика TLS в 2012 году было подвержено такой атаке.

Более того, p и q должны быть выбраны независимо друг от друга. Если p и q совместно используют приблизительно половину своих старших битов, то N может быть вычислено с использованием метода Ферма. На самом деле, даже выбор алгоритма тестирования простоты может иметь последствия для безопасности. Пожалуй, самая широко разрекламированная атака — это уязвимость ROCA в RSALib, которая затронула многие смарт-карты, модули доверенных платформ и даже ключи Yubikey. Здесь при генерации ключей используются только простые числа определенной формы для ускорения вычислений. Простые числа, сгенерированные таким образом, тривиально обнаружить, используя хитрые приемы теории чисел. Как только слабая система была распознана, специальные алгебраические свойства простых чисел позволяют злоумышленнику использовать метод Копперсмита для разложения N.

Стоит учитывать, что ни в одном из этих случаев генерация простых чисел таким образом не является очевидным фактом, приводящем к полному отказу системы. Всё потому, что малозначимые теоретико-числовые свойства простых чисел оказывают существенное влияние на безопасность RSA. Ожидание того, что обыкновенный разработчик будет ориентироваться в этом математическом минном поле, серьезно подрывает безопасность.

Секретная экспонента d

Поскольку использование закрытого ключа большого размера отрицательно влияет на время расшифровки и подписи, у разработчиков есть стимул выбирать небольшую d, особенно в случаях устройств с низким потреблением энергии, таком как смарт-карты. Тем не менее, злоумышленник может восстановить закрытый ключ, когда d меньше корня 4-й степени из N. Вместо этого разработчикам стоит выбирать большое значение d, так, чтобы для ускорения дешифрования могла бы использоваться Китайская теорема об остатках. Однако сложность этого подхода увеличивает вероятность незначительных ошибок реализации, которые могут привести к восстановлению ключа.

Вы скажете, что обычно при инициализации RSA вы сначала генерируете модуль, используете фиксированную открытую экспоненту, а затем выбираете секретную?
Да, это предотвращает атаки с маленькой секретной экспонентой, если вы всегда используете одну из рекомендуемых открытых экспонент e.
К сожалению, это так же предполагает, что разработчики действительно будут этим заниматься. В реальном мире разработчики часто делают странные вещи, например, сначала выбирают d, а потом считают e.

Открытая экспонента e

Как и в случае c секретной экспонентой, разработчики хотят использовать небольшие открытые экспоненты, чтобы сэкономить на шифровании и проверке подписей. Обычно в этом контексте используются простые числа Ферма, в частности e = 3, 17 и 65537.

Несмотря на то, что криптографы рекомендуют использовать 65537, разработчики часто выбирают e = 3, что приводит к множеству уязвимостей в криптосистеме RSA.

(Тут разработчики использовали e = 1, который на самом деле не шифрует открытый текст вообще.)

Когда e = 3 или схожего размера, многое может пойти не так. Маленькие открытые экспоненты часто сочетаются с другими распространенными ошибками, позволяющими злоумышленнику расшифровать определенные шифротексты или факторизовать N.

Например, атака Франклина-Рейтера позволяет злоумышленнику дешифровать два сообщения, которые связаны известным, фиксированным расстоянием. Другими словами, предположим, что Алиса посылает Бобу только «купить» или «продать». Эти сообщения будут связаны известным значением и позволят злоумышленнику определить, какие из них означают «купить», а какие «продать», не расшифровывая сообщения. Некоторые атаки с маленькой e могут даже привести к восстановлению ключа.

Если открытая экспонента маленькая (не только 3), злоумышленник, который знает несколько бит секретного ключа, может восстановить оставшиеся биты и сломать криптосистему. Хотя многие из этих e = 3-атак на RSA можно пофиксить выравниванием (padding), разработчики, которые сами реализуют RSA, чрезвычайно часто забывают его использовать.

Подписи RSA также уязвимы для маленьких публичных экспонент. В 2006 году Блейхенбахер обнаружил атаку, которая позволяет злоумышленникам подделывать произвольные подписи во многих реализациях RSA, в том числе используемых в Firefox и Chrome. Это означает, что любой сертификат TLS из уязвимой реализации может быть подделан. Эта атака использует тот факт, что многие библиотеки используют небольшую публичную экспоненту и не делают простую проверку выравнивания при обработке подписей RSA. Атака Блейхенбахера на подпись настолько проста, что включена во многие упражнения на курсах криптографии.

Выбор параметров — трудная задача

Общим для всех этих атак на параметры является то, что общее количество возможных вариантов параметров намного больше, чем количество безопасных вариантов.

Предполагается, что разработчики сами будут управлять этим сложным процессом отбора, поскольку всё, кроме открытой экспоненты, должно генерироваться при инициализации.
Нет простых способов проверить надежность параметров. Вместо этого разработчикам нужна серьёзная математическая база, наличие которой не следует ожидать от рядовых сотрудников. Хоть использование RSA с выравниванием и может спасти вас при наличии неверных параметров, многие по-прежнему предпочитают этого не делать.

Padding Oracle атаки

Как мы уже выяснили выше, простое использование RSA «из коробки» не совсем работает. Например, схема RSA, изложенная во введении, будет создавать идентичные шифротексты, если один и тот же открытый текст когда-либо шифровался более одного раза. Это проблема, потому что это позволит злоумышленнику узнать содержание сообщения из контекста, не имея возможности расшифровать его. Вот почему нам нужно выравнивать сообщения несколькими случайными байтами. К сожалению, наиболее широко используемая схема выравнивания, PKCS # 1 v1.5, часто уязвима к так называемой атаке padding oracle.

Первоначальная атака на PKCS # 1 v1.5 была обнаружена еще в 1998 году Даниэлем Блейханбахером. Несмотря на то, что ей более 20 лет, сегодня она продолжает быть актуальной для многих систем. Современные версии этой атаки часто включают в себя дополнительный оракул, немного более сложный, чем тот, который первоначально описал Блейханбахер, например, время отклика сервера или выполнение какого-либо понижения версии протокола в TLS. Одним особенно шокирующим примером была атака ROBOT, которая была настолько ужасной, что команда исследователей смогла подписать сообщения секретными ключами Facebook и PayPal. Некоторые могут возразить, что это на самом деле не вина RSA — основная математика в порядке, люди просто испортили важный стандарт несколько десятилетий назад. Дело в том, что у нас уже тогда, с 1998 года была стандартная схема выравнивания с строгим доказательством безопасности, OAEP. Но почти никто не использует ее. Даже когда это происходит, общеизвестно, что OAEP сложно реализовать, и он часто уязвим к атаке Мангера, которая является еще одной атакой оракула, которую можно использовать для восстановления открытого текста.

Фундаментальная проблема здесь заключается в том, что выравнивание необходимо при использовании RSA, и эта дополнительная сложность открывает большой простор для атак на криптосистему. Тот факт, что один бит информации, «правильно ли было выровнено сообщение», может оказать настолько большое влияние на безопасность, что делает разработку защищенных библиотек практически невозможной. TLS 1.3 больше не поддерживает RSA, поэтому мы можем ожидать, что в будущем будет меньше таких атак.

Но пока разработчики будут продолжать использовать RSA в своих собственных приложениях, Padding Oracle атаки будут продолжать происходить.

Что делать?

Люди часто предпочитают использовать RSA, потому что они считают, что это концептуально проще, чем запутанный протокол DSA или криптография с эллиптической кривой (ECC). Но хотя RSA интуитивно понятнее, ему очень не хватает защиты от дурака.

Прежде всего, распространенным заблуждением является то, что эллиптика очень опасна, потому что выбор плохой кривой может всё свести на нет. Верно то, что выбор кривой имеет большое влияние на безопасность, но одним из преимуществ использования ECC является то, что выбор параметров может быть сделан публично. Криптографы делают выбор параметров за вас, так что разработчикам просто нужно генерировать случайные байты данных для использования в качестве ключей. Разработчики теоретически могут построить реализацию ECC с ужасными параметрами и не смогут проверить наличие таких вещей, как некорректные точки кривой, но они, как правило, этого не делают. Вероятное объяснение состоит в том, что математика, стоящая за ECC, настолько сложна, что очень немногие люди чувствуют себя достаточно уверенно, чтобы ее реализовать. Другими словами, этот страх заставляет людей использовать библиотеки, созданные криптографами, которые знают своё дело. RSA, с другой стороны, настолько прост, что его можно (плохо) реализовать за час.

Во-вторых, любое согласование ключей на основе алгоритма Диффи-Хеллмана или схема подписи (включая варианты эллиптической кривой) не требуют выравнивания и, следовательно, полностью устойчивы к атакам Padding Oracle. Это серьезная победа, учитывая, что у RSA очень длинный послужной список попыток избежать этого класса уязвимостей.

Мы рекомендуем использовать Curve25519 для обмена ключами и ed25519 для цифровых подписей. Шифрование должно выполняться с использованием протокола ECIES, который сочетает в себе обмен ключами ECC с алгоритмом симметричного шифрования. Curve25519 была разработана чтобы полностью предотвратить классы атак, которые могут случиться с другими кривыми, а еще она очень быстрая. Более того, она реализована во множестве библиотек, например libsodium, который снабжен легкой для чтения документацией и доступен для большинства языков.

Хватит использовать RSA. Серьезно.

(Twilio до сих пор использует RSA ключи)

(Travis CI до сих пор использует 1024 битные ключи и не даёт их заменить)

RSA был важной вехой в развитии безопасных коммуникаций, но последние два десятилетия криптографических исследований сделали его устаревшим. Алгоритмы на эллиптических кривых как для обмена ключами, так и для цифровых подписей были стандартизированы еще в 2005 году и с тех пор были интегрированы в интуитивно понятные и устойчивые к неправильному использованию библиотеки, такие как libsodium. Тот факт, что RSA все еще широко используется в наши дни, указывает как на ошибку со стороны криптографов из-за неадекватного описания рисков, присущих RSA, так и со стороны разработчиков, переоценивающих свои способности успешно развертывать его. Security сообщество должно начать думать об этом как о стадной проблеме — хоть некоторые из нас и могут быть в состоянии ориентироваться в чрезвычайно опасном процессе настройки или реализации RSA, исключения дают понять разработчикам, что в некотором роде RSA еще актуален. Несмотря на множество предостережений и предупреждений на StackExchange и GitHub README, очень немногие люди верят, что именно они испортят RSA, и поэтому они продолжают поступать безрассудно. В конечном счете ваши пользователи будут платить за это. Вот почему мы все должны согласиться с тем, что использование RSA в 2019 году совершенно неприемлемо. Без исключений.

Оригинал статьи на английском.

VirgilSecurity, Inc. разрабатывает open source developer friendly SDK и сервисы для защиты данных. Мы позволяем разработчикам использовать существующие алгоритмы с минимальным риском для безопасности.

Источник