Комплексные числа

Комплексные числа. Комплексным числом называется число вида z=a+biabRi2=−1

Замечание. Если a=ReZ=0b=Imz=0, то число z называется мнимым. Если a=ReZ=0b=Imz=0, то число z называется чисто мнимым

Свойство. Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:z+z=2azz=a2+b2

Противоположные числа. Числа z=a+bi и −z=−a−bi называются противоположными комплексными числами.

Свойство. Сумма двух противоположных комплексных чисел равна нулю:
z+(−z)=0

Равные числа. Два комплексных числа называются равными, если равны их действительные и мнимые части.

Действия с комплексными числами, заданными в алгебраической форме:

Свойство сложения: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2=a+bi+c+di=a+c+(b+d)i
Пример: 5+3i+3−i=8+2i

Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2=a+bi−c+di=a−c+(b−d)i

Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1z2=a+bic+di=ac−bd+(ad+bc)i

Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число видаz=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi

Действия с комплексными числами, заданных в тригонометрической форме
Запись комплексного числа z = a + bi в виде z=rcos+isin называется тригонометрической формой комплексного числа.

Модуль комплексного числа: r=a2+b2

где a, b – действительные числа, i – мнимая единица.

Источник

Методичесое пособие «Комплексные числа» для системы ДО и профессиональных классов

Разделы: Математика

Во многих разделах математики и ее приложениях невозможно ограничиться лишь рассмотрением действительных чисел. Например, решение уравнений типа х 2 +х+1=0, х 2 +1=0.

Для их решения надо расширить множество действительных чисел и таким расширением являются комплексные числа.

Комплексные числа часто называют мнимыми. Это название объясняется тем, что, хотя стали употребляться еще в XVI веке, они долго продолжали называться даже выдающимися математиками чем-то реально не существующими, мнимыми в буквальном смысле. Одному из создателей дифференциального и интегрального исчисления, немецкому математику Г. Лейбницу (1646–1716) принадлежат, например, такие слова:

“Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием”.

Но уже во времена К. Гаусса (1777–1855) было дано геометрическое истолкование комплексных чисел как точек плоскости. Трудами выдающихся математиков XIX века О. Коши, Б. Римана, К. Вейерштрасса на базе комплексных чисел была построена одна из самых красивых математических дисциплин – Теория функций комплексной переменной.

II. Определение комплексного числа.

Комплексные числа часто обозначают одной буквой, причем обычно используют буквы z и ω.

Равенство z=a+bi называют алгебраической формой записи числа z.

Частное чисел z₂ и z₁ при условии z₁≠0 понимается следующее комплексное число:

Заметим что число 0+bi называют чисто мнимым и записывают bi,

Если b=0, то число a просто действительное.

Действительная часть числа z=a+bi обозначается Rez.

Мнимая часть числа z обозначается Imz.

Пример 3 i 3 =i*i*i=-i, i 4 =i*i*i*i=1.

III. Геометрическая интерпретация комплексных чисел. Модуль и аргументы комплексного числа.

Рис.1

Хорошо известно, что между множеством действительных чисел и множеством точек прямой можно установить взаимно однозначное соответствие. Геометрическую интерпретацию можно использовать и при изучении комплексных чисел.

Каждому комплексному числу z=a+bi можно поставить в соответствие точку M(a,b) координатной плоскости.

Сама координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, а ось ординат мнимой осью.

Число z=a+bi есть вектор , исходящий из начала координат О(0,0) и идущий в точку M(a,b).

При сложении z₁ и z₂ складываются их действительные и мнимые части. При сложении складываются их координаты.

Модулем комплексного числа называется длина вектора соответствующего этому числу и обозначается │ Z│.

называется комплексно сопряженным числу z=a+bi. Тогда имеем: . Произведение сопряженных чисел равно квадрату модуля.

Аргументы комплексного числа.

Комплексные числа имеющие один и тот же модуль │ Z│ = r, соответствуют, очевидно, точкам плоскости расположенными на окружности радиуса r с центром в точке z=0.

Рис. 2

Определение. Аргументом комплексного числа z≠0 называется величина угла между положительным направлением действительной оси и вектором , причем величина угла считается положительной, если отчет ведется против часовой стрелки и отрицательным, если отчет ведется по часовой стрелке. Для обозначения аргументов комплексного числа z=a+bi используют обозначения arg(a+bi) или argz. Аргумент комплексного числа z определяется не однозначно.

Любые два аргумента комплексного числа отличаются друг от друга слагаемым кратным 2π.

IV. Тригонометрическая форма записи комплексного числа. Операции над комплексными числами.

Помимо алгебраической формы используются и другие формы записи комплексных чисел – тригонометрическая форма и показательная форма записи комплексных чисел.

Рассмотрим тригонометрическую форму записи.

Действительная и мнимая части комплексного числа z=a+bi выражаются через его модуль │ Z│ =r и аргумент φ следующим образом (рис.2).

Поэтому комплексное число z может быть записано в следующем виде: z= r(cos φ + isin φ )

Такая запись называется тригонометрической формой записи.

Для того чтобы перейти от алгебраической формы z=a+bi к тригонометрической форме записи числа, достаточно найти его модуль и один из аргументов. Модуль определяется по формуле:

Записать число z=1-I в тригонометрической форме.

Одним из решений этой системы будет:

но эти записи будут являться алгебраической, а не тригонометрической формой записи комплексного числа.

Умножение и деление комплексных чисел записанных в тригонометрической форме.

Таким образом: модуль произведения двух комплексных чисел равен произведению модулей, сумма аргументов есть аргумент произведения.

Следовательно, модуль частного двух комплексных чисел равен частному этих модулей, разность аргументов делимого и делителя является аргументом частного.

Модуль произведения n комплексных чисел равен произведению всех сомножителей, сумма аргументов всех сомножителей является аргументом произведения. Отсюда, как частный случай, получается формула, которая носит название формулы Муавра.

(r(cosφ+isinφ)) n =r n (cosnφ+isinφn)

Перейдем к операции извлечения корня из данной степени комплексного числа.

Число z является корнем степени n из числа ω, если z n =ω.

Из данного определения вытекает, что каждое решение уравнения z n =ω является корнем n из числа ω.

Пусть ω≠0, тогда z=r( cosφ + isinφ ), ω =s( cosψ + isinψ )

Уравнение z n = ω запишем в виде: r n ( cosnφ + isinφn )=s( cosψ + isinψ )

Два комплексных числа равны, когда равны их модули, а аргументы различаются слагаемым кратным 2π, то есть r n =s и nφ=ψ+2π k

как пара комплексных чисел i и –i.

Найти все значения . Запишем число ω =-16 в тригонометрической форме ω=16( cosπ + isinπ ).

Точки z₀,z_1,z_2,z₃ есть вершины квадрата вписанного в окружность радиуса 2.

V. Квадратные уравнения.

Рассмотрим уравнение: ax 2 +bx+c=0, a≠0

Решим это уравнение в комплексных числах, тогда, если D˂0, мы получаем решение в комплексных числах:

Над множеством комплексных чисел справедлива основная теорема алгебры : алгебраическое уравнение n – степени имеет ровно n корней.

VI. Комплексная степень числа e. Показательная форма записи.

Возведем e в степень z, где z=x+iy.e z =e x e iy =e x (cosy+isiny).

Доказательство данной формулы основано на разложении элементарных функций в ряд Тейлора в окрестности нуля.

Источник

Электронная библиотека

Действительные числа x и y называются соответственно действительной и мнимой частью комплексного числа z и обозначаются:

Множество комплексных чисел обозначают буквой С.

Например, – комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.

Пример 1

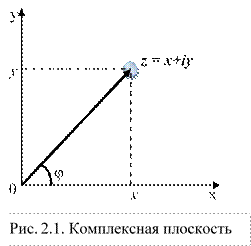
Таким образом, между множеством C и множеством векторов (и точек!) плоскости xOy устанавливается взаимно однозначное соответствие.

Определения. Плоскость xОy называется плоскостью комплексных чисел (или просто комплексной плоскостью), будем её обозначать Z. Ось Ox – действительная ось; ось Oy – мнимая ось.

Поскольку – вектор, то он имеет длину и характеризуется направлением.

Длину вектора называют модулем комплексного числа z = х + iy, а величину угла наклона вектора по отношению к оси Ox – аргументом z. Их обозначают символами:

Модуль комплексного числа есть однозначная функция:

Из рисунка 2.1 видно, что:

Аргумент есть функция многозначная. Все значения аргумента удовлетворяют соотношению:

Из формул (2.5) и (2.6) следует:

Пример 2

Необходимо: найти модуль комплексного числа, изобразить число на комплексной плоскости, найти главное значение аргумента комплексного числа.

Используем формулу (*) и находим модуль комплексного числа:

Изобразим число на комплексной плоскости (рис. 2.2).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Числа. Комплексные (мнимые) числа.

Множество всех комплексных чисел с арифметическими операциями есть поле и обычно обозначают как .

Мнимое число (либо чисто мнимое число) — комплексное число с действительной частью, равной нулю. Раньше этим термином обозначали комплексные числа.

Комплексные числа изображаются на комплексной плоскости:

Например, построим на комплексной плоскости следующие комплексные числа:

, , ,

, , ,

, , , .

Действия над комплексными числами.

означает, что a = c и b = d (2 комплексных числа равны между собой только в том случае, если равны их действительные и мнимые части).

(a + bi) + (c + di) = (a + c) + (b + d)i.

Для того чтобы сложить 2 комплексных числа нужно сложить их действительные и мнимые части:

(a + bi) – (c + di) = (a – c) + (b – d)i.

Действие аналогично сложению, отличие только в том, что вычитаемое берем в скобки, а потом – как обычно раскрываем их со сменой знака:

У числа, которое мы получили 2, а не 3 части. Так как действительная часть является составной: . Что было понятней ответ перепишем так: .

Рассчитываем 2-ю разность:

Здесь действительная часть тоже составная: .

Приведем короткий пример с «нехорошей» мнимой частью: . В этом случае без скобок никак не обойтись.

Найдем произведение комплексных чисел ,

Раскрываем скобки, как обычно. Обратите внимание, что и будьте внимательны.

Напомним: Чтобы умножить многочлен на многочлен надо все члены 1-го многочлена умножить на каждый член другого многочлена.

Очевидно, что .

Как и в сумме, в произведении комплексных чисел работает перестановочный закон: .

Произведение 2-х сопряжённых комплексных чисел равно положительному действительному числу.

Если делитель ненулевой, деление всегда возможно.

Есть комплексные числа , . Найдем частное .

Деление чисел производится способом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Напомним, что и смотрим на наш знаменатель: . В знаменателе уже имеется , поэтому сопряженным выражением в данном случае оказывается , т.е. .

Из правила, знаменатель необходимо домножить на , и, чтобы ничего не изменилось, умножить числитель на такое же число :

Дальше в числителе раскрываем скобки. А в знаменателе пользуемся формулой (при ).

Часто перед делением дробь лучше упростить.

Свойства комплексных чисел.

1. Основная теорема алгебры.

У всех, не являющихся константой многочленов (от одной переменной) с комплексными коэффициентами есть как минимум 1 корень в поле комплексных чисел.

2. Формула Муавра и извлечение корней из комплексных чисел.

Эта формула помогает возводить в целую степень комплексное число, не равное нулю, которое представлено в тригонометрической форме.

Формула Муавра имеет вид:

где r — модуль, а φ — аргумент комплексного числа.

Аналогичная формула применяется также и при вычислении корней n-ой степени из комплексного числа, не равного нулю:

Заметим, что корни n-й степени из комплексного числа, не равного нулю, всегда есть, и их чило равно n. На комплексной плоскости, как видно из формулы, все эти корни оказываются вершинами правильного n-угольника, который вписан в окружность радиуса с центром в начале координат.

Например, корни 5-ой степени из единицы (вершины пятиугольника):

Источник

Числа. Геометрическое представление комплексных чисел.

Комплексным числом z является пара действительных чисел x и y, упорядоченная.

Первое число x из этой пары является действительной частью комплексного числа z и обозначают его как Rez, x = Rez. Второе число y является мнимой частью комплексного числа z и обозначают его как Imz, y = Imz.

Действительные числа изображают точками на числовой прямой:

Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого, комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b. Эта система координат называется комплексной плоскостью.

Модуль комплексного числа a + bi обозначают |a+ bi| либо буквой r и он равняется:

У сопряженных комплексных чисел равные модули.

Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi выражают через модуль этого числа r и аргумент φ:

Операции с комплексными числами, которые представлены в тригонометрической форме.

Это знаменитая формула Муавра.

Чтобы получить n разных значений корня n-ой степени из z нужно задать n последовательных значений для k (к примеру, k = 0, 1, 2,…, n – 1).

Источник