Silhouette score что это
Оценка качества в задаче кластеризации
Проблема оценки качества в задаче кластеризации трудноразрешима, как минимум, по двум причинам:
Содержание
Методы оценки качества кластеризации [ править ]
Метод оценки качества кластеризации — инструментарий для количественной оценки результатов кластеризации.
Принято выделять две группы методов оценки качества кластеризации:
Внешние меры оценки качества [ править ]
Данные меры используют дополнительные знания о кластеризуемом множестве: распределение по кластерам, количество кластеров и т.д.
Обозначения [ править ]
[math]\begin
Индекс Rand [ править ]
Индекс Rand оценивает, насколько много из тех пар элементов, которые находились в одном классе, и тех пар элементов, которые находились в разных классах, сохранили это состояние после кластеризации алгоритмом.
Имеет область определения от 0 до 1, где 1 — полное совпадение кластеров с заданными классами, а 0 — отсутствие совпадений.
Индекс Adjusted Rand [ править ]
где [math]n_
Индекс Жаккара (англ. Jaccard Index) [ править ]
Индекс Жаккара похож на Индекс Rand, только не учитывает пары элементов находящиеся в разные классах и разных кластерах ( [math]TN[/math] ).
[math] Jaccard = \dfrac
Имеет область определения от 0 до 1, где 1 — полное совпадение кластеров с заданными классами, а 0 — отсутствие совпадений.
Индекс Фоулкса – Мэллова (англ. Fowlkes-Mallows Index) [ править ]
Индекс Фоулкса – Мэллова используется для определения сходства между двумя кластерами.
Более высокое значение индекса означает большее сходство между кластерами. Этот индекс также хорошо работает на зашумленных данных.
Hubert Г statistic [ править ]
Данная мера отражает среднее расстояние между объектами разных кластеров:
[math] Г = \dfrac<1>
Чем больше значение меры — тем лучше.
Индекс Phi [ править ]
Классическая мера корреляции между двумя переменными:
Minkowski Score [ править ]
Индекс Гудмэна-Крускала (англ. Goodman-Kruskal Index) [ править ]
Entropy [ править ]
Энтропия измеряет «чистоту» меток классов:
Стоит отметить, что если все кластера состоят из объектов одного класса, то энтропия равна 0.
Purity [ править ]
Чистота ставит в соответствие кластеру самый многочисленный в этом кластере класс.
[math] P = \sum_i p_i ( \max_j \dfrac < p_
Чистота находится в интервале [0, 1], причём значение = 1 отвечает оптимальной кластеризации.
F-мера [ править ]
F-мера представляет собой гармоническое среднее между точностью (precision) и полнотой (recall).
[math] F = \sum_j p_j \max_i \big\lbrack 2 \dfrac < p_
Variation of Information [ править ]
Данная мера измеряет количество информации, потерянной и полученной при переходе из одного кластера в другой.
Внутренние меры оценки качества [ править ]
Данные меры оценивают качество структуры кластеров опираясь только непосредственно на нее, не используя внешней информации.
Компактность кластеров (англ. Cluster Cohesion) [ править ]
Идея данного метода в том, что чем ближе друг к другу находятся объекты внутри кластеров, тем лучше разделение.
Таким образом, необходимо минимизировать внутриклассовое расстояние, например, сумму квадратов отклонений:
Отделимость кластеров (англ. Cluster Separation) [ править ]
В данном случае идея противоположная — чем дальше друг от друга находятся объекты разных кластеров, тем лучше.
Поэтому здесь стоит задача максимизации суммы квадратов отклонений:
Индекс Данна (англ. Dunn Index) [ править ]
Индекс Данна имеет множество вариаций, оригинальная версия выглядит следующим образом:
Обобщенный Индекс Данна (gD31, gD41, gD51, gD33, gD43, gD53) [ править ]
Все эти вариации являются комбинациями 3 вариантов вычисления оценки разделения [math]\delta[/math] и оценки компактности [math]\Delta[/math]
Обобщенный индекс Данна, как и обычный, должен возрастать вместе с улучшением качества кластеризации.
Индекс S_Dbw [ править ]
Основан на вычислении Евклидовой нормы
и стандартных отклонений
Сам индекс определяется формулой:
Должен снижаться с улучшением кластеризации.
Силуэт (англ. Silhouette) [ править ]
Значение силуэта показывает, насколько объект похож на свой кластер по сравнению с другими кластерами.
Оценка для всей кластерной структуры:
Можно заметить, что
Чем ближе данная оценка к 1, тем лучше.
Есть также упрощенная вариация силуэта: [math]a(x_i, c_k)[/math] и [math]b(x_i, c_k)[/math] вычисляются через центры кластеров.
Индекс Calinski–Harabasz [ править ]
Индекс C [ править ]
Индекс C представляет собой нормализованную оценку компактности:
Индекс Дэвиcа-Болдуина (англ. Davies–Bouldin Index) [ править ]
Существует еще одна вариация данной меры, которая была предложена автором вместе с основной версией:
C-индекс и индекс Дэвиcа-Болдуина должны минимизироваться для роста кластеризации.
Score function [ править ]
Индекс, основанный на суммировании. Здесь оценка компактности выражается в дистанции от точек кластера до его центроида, а оценка разделимости — в дистанции от центроидов кластеров до глобального центроида.
Чтобы функция оценки была эффективной, она должна максимизировать bcd, минимизировать wcd и быть ограниченной. Чем больше данный индекс, тем выше качество.
Индекс Gamma [ править ]
Индекс COP [ править ]
В данной мере компактность вычисляется как расстояние от точек кластера до его центроиды, а разделимость основана на расстоянии до самого отдаленного соседа.
Индекс CS [ править ]
Был предложен в области сжатия изображений, но может быть успешно адаптирован для любого другого окружения. Он оценивает компактность по диаметру кластера, а отделимость — как дистанцию между ближайшими элементами двух кластеров.
Чем меньше значение данного индекса, тем выше качество кластеризации.
Индекс Sym [ править ]
Чем выше данное значение, тем лучше.
Индексы SymDB, SymD, Sym33 [ править ]
Модифицируют оценку компактности для индексов Дэвиса-Боулдина, Данна и gD33 соответственно.
SymDB вычисляется аналогично DB с изменением вычисления [math]S[/math] на:
Данная оценка должна уменьшаться для улучшения качества кластеризации.
В SymD переопределена функция [math]\Delta[/math] :
в Sym33 аналогично SymD переопределена [math]\Delta[/math] :
Последние две оценки должны расти для улучшения качества кластеризации.
Negentropy increment [ править ]
В отличие от подавляющего большинства других оценок, не основывается на сравнении компактности и разделимости. Определяется следующим образом:
Данная оценка должна уменьшаться пропорционально росту качества кластеризации.
Индекс SV [ править ]
Одна из самых новых из рассматриваемых в данном разделе оценок. Измеряет разделимость по дистанции между ближайшими точка кластеров, а компактность — по расстоянию от пограничных точек кластера до его центроида.
Данная оценка должна увеличиваться.
Индекс OS [ править ]
Отличается от предыдущей оценки усложненным способом вычисления оценки разделимости.
Функции [math]a[/math] и [math]b[/math] определены следующим образом:
Данная оценка, как и предыдущая, должна возрастать.
Сравнение [ править ]
В Таблице 1 приведены оценки сложности мер качества кластеризации ( [math]n[/math] — число объектов в рассматриваемом наборе данных):
| [math]Davies-Bouldin[/math] | [math]O(n\log | [math]CS[/math] | [math]O(n\log |
| [math]Dunn[/math] | [math]O(n^2)[/math] | [math]DB^*[/math] | [math]O(n\log |
| [math]Calinski-Harabasz[/math] | [math]O(n\log | [math]SF[/math] | [math]O(n)[/math] |
| [math]Sillhouette[/math] | [math]O(n^2)[/math] | [math]Sym[/math] | [math]O(n^2)[/math] |
| [math]gD31[/math] | [math]O(n^2)[/math] | [math]COP[/math] | [math]O(n^2)[/math] |
| [math]gD41[/math] | [math]O(n^2)[/math] | [math]SV[/math] | [math]O(n\log |
| [math]gD51[/math] | [math]O(n^2)[/math] | [math]OS[/math] | [math]O(n^2\log |
| [math]gD33[/math] | [math]O(n^2)[/math] | [math]SDbw[/math] | [math]O(n\log |
| [math]gD43[/math] | [math]O(n^2)[/math] | [math]C-index[/math] | [math]O(n^2\log |
| [math]gD53[/math] | [math]O(n\log |
Силуэт Индекс — кластерный индекс достоверности | Набор 2
Многие интересные алгоритмы применяются для анализа очень больших наборов данных. Большинство алгоритмов не предоставляют никаких средств для его проверки и оценки. Поэтому очень сложно сделать вывод, какие кластеры являются лучшими и должны быть приняты для анализа.
Есть несколько показателей для прогнозирования оптимальных кластеров —
Теперь, давайте обсудим внутренний индекс кластера валидность Silhouette Index.
Силуэт Индекс —
Силуэтный анализ относится к методу интерпретации и проверки согласованности в кластерах данных. Значение силуэта является мерой того, насколько объект похож на свой собственный кластер (сплоченность) по сравнению с другими кластерами (разделение). Он может быть использован для изучения расстояния между результирующими кластерами. График силуэта показывает меру того, насколько близко каждая точка в одном кластере находится к точкам в соседних кластерах, и, таким образом, предоставляет способ визуальной оценки таких параметров, как количество кластеров.
The Silhouette validation technique calculates the silhouette index for each sample, average silhouette index for each cluster and overall average silhouette index for a dataset. Using the approach each cluster could be represented by Silhouette index, which is based on the comparison of its tightness and separation.
Расчет стоимости силуэта —
Если значение индекса Silhouette высокое, объект сопоставляется с собственным кластером и плохо сопоставляется с соседними кластерами. Коэффициент Силуэт рассчитывается с использованием среднего расстояния внутри кластера (а) и среднего расстояния до ближайшего кластера (b) для каждой выборки. Коэффициент Силуэт определяется как —
S (i) = (b (i) — a (i)) / (max
Диапазон значения силуэта —
Теперь, очевидно, S (i) будет лежать между [-1, 1] —
Ниже приведена реализация вышеприведенного Silhouette Index на Python:
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# Генерация примера данных из make_blobs
for n_clusters in no_of_clusters:
cluster = KMeans(n_clusters = n_clusters)
# среднее значение для всех образцов.
silhouette_avg = silhouette_score(X, cluster_labels)
KMeans Silhouette Score Explained With Python Example
In this post, you will learn about the concepts of KMeans Silhouette Score in relation to assessing the quality of K-Means clusters fit on the data.
Join the DZone community and get the full member experience.
In this post, you will learn about the concepts of KMeans Silhouette Score concerning assessing the quality of K-Means clusters fit on the data. As a data scientist, it is of utmost importance to understand the concepts of the Silhouette score as it would help in evaluating the quality of clustering done using the K-Means algorithm. In this post, the following topics will be covered:
You may want to check some of the following posts in relation to clustering:
Introduction to Silhouette Score Concepts
Silhouette score is used to evaluate the quality of clusters created using clustering algorithms such as K-Means in terms of how well samples are clustered with other samples that are similar to each other. The Silhouette score is calculated for each sample of different clusters. To calculate the Silhouette score for each observation/data point, the following distances need to be found out for each observations belonging to all the clusters:
Silhouette score, S, for each sample is calculated using the following formula:
Silhouette Score Explained Using Python Example
The Python Sklearn package supports the following different methods for evaluating Silhouette scores.
We will learn about the following in relation to Silhouette score:
Calculate Silhouette Score for K-Means Clusters With n_clusters = N
Here is the code calculating the silhouette score for the K-means clustering model created with N = 3 (three) clusters using the Sklearn IRIS dataset.
Executing the above code predicts the Silhouette score of 0.55.
Perform Comparative Analysis to Determine Best Value of K Using Silhouette Plot
Yellowbrick extends the Scikit-Learn API to make a model selection and hyperparameter tuning easier. It provides some very useful wrappers to create the visualization in no time. Here is the code to create a Silhouette plot for K-Means clusters with n_cluster as 2, 3, 4, 5.
Executing the above code will result in the following Silhouette plots for 2, 3, 4, and 5 clusters:
Fig 1. Silhouette Analysis for 2, 3, 4, 5 Clusters
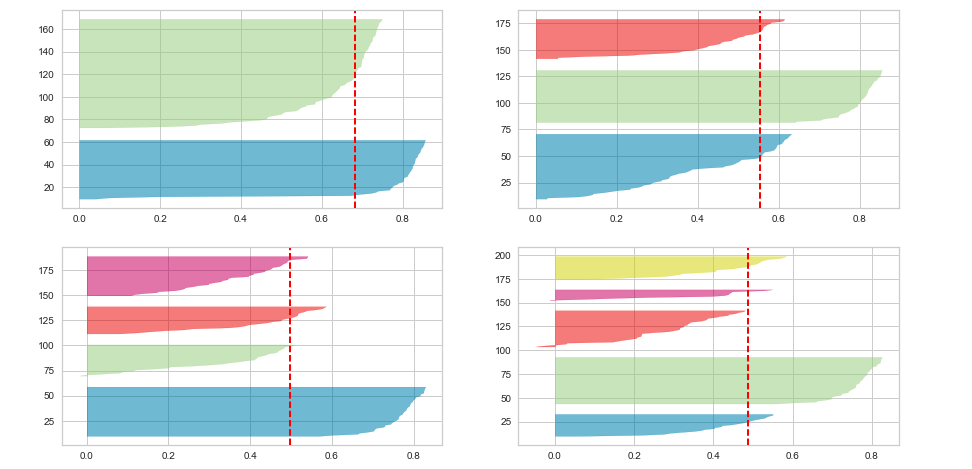
Here is the Silhouette analysis done on the above plots to select an optimal value for n_clusters.
Conclusions
Here is the summary of what you learned in this post in relation to silhouette score concepts:
Открытый курс машинного обучения. Тема 7. Обучение без учителя: PCA и кластеризация
Привет всем! Приглашаем изучить седьмую тему нашего открытого курса машинного обучения!
Данное занятие мы посвятим методам обучения без учителя (unsupervised learning), в частности методу главных компонент (PCA — principal component analysis) и кластеризации. Вы узнаете, зачем снижать размерность в данных, как это делать и какие есть способы группирования схожих наблюдений в данных.
UPD: теперь курс — на английском языке под брендом mlcourse.ai со статьями на Medium, а материалами — на Kaggle (Dataset) и на GitHub.
Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).
План этой статьи
0. Введение
Основное отличие методов обучения без учителя от привычных классификаций и регрессий машинного обучения в том, что разметки для данных в этом случае нет. От этого образуются сразу несколько особенностей — во-первых это возможность использования несопоставимо больших объёмов данных, поскольку их не нужно будет размечать руками для обучения, а во-вторых это неясность измерения качества методов, из-за отсутствия таких же прямолинейных и интуитивно понятных метрик, как в задачах обучения с учителем.
Одной из самых очевидных задач, которые возникают в голове в отсутствие явной разметки, является задача снижения размерности данных. С одной стороны её можно рассматривать как помощь в визуализации данных, для этого часто используется метод t-SNE, который мы рассмотрели во второй статье курса. С другой стороны подобное снижение размерности может убрать лишние сильно скоррелированные признаки у наблюдений и подготовить данные для дальнейшей обработки в режиме обучения с учителем, например сделать входные данные более «перевариваемыми» для деревьев решений.
1. Метод главных компонент (PCA)
Интуиция, теория и особенности применения
Метод главных компонент (Principal Component Analysis) — один из самых интуитивно простых и часто используемых методов для снижения размерности данных и проекции их на ортогональное подпространство признаков.
В совсем общем виде это можно представить как предположение о том, что все наши наблюдения скорее всего выглядят как некий эллипсоид в подпространстве нашего исходного пространства и наш новый базис в этом пространстве совпадает с осями этого эллипсоида. Это предположение позволяет нам одновременно избавиться от сильно скоррелированных признаков, так как вектора базиса пространства, на которое мы проецируем, будут ортогональными.
В общем случае размерность этого эллипсоида будет равна размерности исходного пространства, но наше предположение о том, что данные лежат в подпространстве меньшей размерности, позволяет нам отбросить «лишнее» подпространство в новой проекции, а именно то подпространство, вдоль осей которого эллипсоид будет наименее растянут. Мы будем это делать «жадно», выбирая по-очереди в качестве нового элемента базиса нашего нового подпространства последовательно ось эллипсоида из оставшихся, вдоль которой дисперсия будет максимальной.
«To deal with hyper-planes in a 14 dimensional space, visualize a 3D space and say ‘fourteen’ very loudly. Everyone does it.» — Geoffrey Hinton
Рассмотрим как это делается математически:
Чтобы снизить размерность наших данных из 
в 
, нам нужно выбрать топ- 
осей такого эллипсоида, отсортированные по убыванию по дисперсии вдоль осей.
Начнём с того, что посчитаем дисперсии и ковариации исходных признаков. Это делается просто с помощью матрицы ковариации. По определению ковариации, для двух признаков 
и 
их ковариация будет
где 
— матожидание 
-ого признака.
При этом отметим, что ковариация симметрична и ковариация вектора с самим собой будет равна его дисперсии.
Таким образом матрица ковариации представляет собой симметричную матрицу, где на диагонали лежат дисперсии соответствующих признаков, а вне диагонали — ковариации соответствующих пар признаков. В матричном виде, где 
это матрица наблюдений, наша матрица ковариации будет выглядеть как
Чтобы освежить память — у матриц как у линейных операторов есть такое интересное свойство как собственные значения и собственные вектора (eigenvalues и eigenvectors). Эти штуки замечательны тем, что когда мы нашей матрицей действуем на соответствующее линейное пространство, собственные вектора остаются на месте и лишь умножаются на соответствующие им собственные значения. То есть определяют подпространство, которое при действии этой матрицей как линейным оператором, остаётся на месте или «переходит в себя». Формально собственный вектор 
с собственным значением 
для матрицы 
определяется просто как 
.
Матрицу ковариации для нашей выборки можно представить в виде произведения 
. Из отношения Релея вытекает, что максимальная вариация нашего набора данных будет достигаться вдоль собственного вектора этой матрицы, соответствующего максимальному собственному значению. Таким образом главные компоненты, на которые мы бы хотели спроецировать наши данные, являются просто собственными векторами соответствующих топ- штук собственных значений этой матрицы.
Дальнейшие шаги просты до безобразия — надо просто умножить нашу матрицу данных на эти компоненты и мы получим проекцию наших данных в ортогональном базисе этих компонент. Теперь если мы транспонируем нашу матрицу данных и матрицу векторов главных компонент, мы восстановим исходную выборку в том пространстве, из которого мы делали проекцию на компоненты. Если количество компонент было меньше размерности исходного пространства, мы потеряем часть информации при таком преобразовании.
Примеры использования
Набор данных по цветкам ириса
Начнём с того, что загрузим все необходимые модули и покрутим привычный датасет с ирисами по примеру из документации пакета scikit-learn.
Теперь посмотрим, насколько PCA улучшит результаты для модели, которая в данном случае плохо справится с классификацией из-за того, что у неё не хватит сложности для описания данных:
Теперь попробуем сделать то же самое, но с данными, для которых мы снизили размерность до 2D:
Смотрим на возросшую точность классификации:
Видно, что качество возросло незначительно, но для более сложных данных более высокой размерности, где данные не разбиваются тривиально вдоль одного признака, применение PCA может достаточно сильно улучшить качество работы деревьев решений и ансамблей на их основе.
Посмотрим на 2 главные компоненты в последнем PCA-представлении данных и на тот процент исходной дисперсии в даных, который они «объясняют».
Набор данных по рукописным цифрам
Теперь возьмем набор данных по рукописным цифрам. Мы с ним уже работали в 3 статье про деревья решений и метод ближайших соседей.
Вспомним, как выглядят эти цифры – посмотрим на первые десять. Картинки здесь представляются матрицей 8 x 8 (интенсивности белого цвета для каждого пикселя). Далее эта матрица «разворачивается» в вектор длины 64, получается признаковое описание объекта.
Получается, размерность признакового пространства здесь – 64. Но давайте снизим размерность всего до 2 и увидим, что даже на глаз рукописные цифры неплохо разделяются на кластеры.
Ну, правда, с t-SNE картинка получается еще лучше, поскольку у PCA ограничение – он находит только линейные комбинации исходных признаков. Зато даже на этом относительно небольшом наборе данных можно заметить, насколько t-SNE дольше работает.
На практике, как правило, выбирают столько главных компонент, чтобы оставить 90% дисперсии исходных данных. В данном случае для этого достаточно выделить 21 главную компоненту, то есть снизить размерность с 64 признаков до 21.
2. Кластеризация
Интуитивная постановка задачи кластеризации довольно проста и представляет из себя наше желание сказать: «Вот тут у меня насыпаны точки. Я вижу, что они сваливаются в какие-то кучки вместе. Было бы круто иметь возможность эти точки относить к кучкам и в случае появления новой точки на плоскости говорить, в какую кучку она падает.» Из такой постановки видно, что пространства для фантазии получается много, и от этого возникает соответствующее множество алгоритмов решения этой задачи. Перечисленные алгоритмы ни в коем случае не описывают данное множество полностью, но являются примерами самых популярных методов решения задачи кластеризации.
K-means
Алгоритм К-средних, наверное, самый популярный и простой алгоритм кластеризации и очень легко представляется в виде простого псевдокода:
В случае обычной евклидовой метрики для точек лежащих на плоскости, этот алгоритм очень просто расписывается аналитически и рисуется. Давайте посмотрим соответствующий пример:
Также стоит заметить, что хоть мы и рассматривали евклидово расстояние, алгоритм будет сходиться и в случае любой другой метрики, поэтому для различных задач кластеризации в зависимости от данных можно экспериментировать не только с количеством шагов или критерием сходимости, но и с метрикой, по которой мы считаем расстояния между точками и центроидами кластеров.
Другой особенностью этого алгоритма является то, что он чувствителен к исходному положению центроид кластеров в пространстве. В такой ситуации спасает несколько последовательных запусков алгоритма с последующим усреднением полученных кластеров.
Выбор числа кластеров для kMeans
В отличие от задачи классификации или регресии, в случае кластеризации сложнее выбрать критерий, с помощью которого было бы просто представить задачу кластеризации как задачу оптимизации.
В случае kMeans распространен вот такой критерий – сумма квадратов расстояний от точек до центроидов кластеров, к которым они относятся.
здесь 
– множество кластеров мощности 
, 
– центроид кластера 
.
Понятно, что здравый смысл в этом есть: мы хотим, чтобы точки располагались кучно возле центров своих кластеров. Но вот незадача: минимум такого функционала будет достигаться тогда, когда кластеров столько же, сколько и точек (то есть каждая точка – это кластер из одного элемента).
Для решения этого вопроса (выбора числа кластеров) часто пользуются такой эвристикой: выбирают то число кластеров, начиная с которого описанный функционал 
падает «уже не так быстро». Или более формально:
Видим, что 
падает сильно при увеличении числа кластеров с 1 до 2 и с 2 до 3 и уже не так сильно – при изменении с 3 до 4. Значит, в данной задаче оптимально задать 3 кластера.
Сложности
Само по себе решение задачи K-means NP-трудное (NP-hard), и для размерности 
, числа кластеров и числа точек решается за 
. Для решения такой боли часто используются эвристики, например MiniBatch K-means, который для обучения использует не весь датасет целиком, а лишь маленькие его порции (batch) и обновляет центроиды используя среднее за всю историю обновлений центроида от всех относящихся к нему точек. Сравнение обычного K-means и его MiniBatch имплементации можно посмотреть в документации scikit-learn.
Affinity Propagation
Ещё один пример алгоритма кластеризации. В отличие от алгоритма К-средних, данный подход не требует заранее определять число кластеров, на которое мы хотим разбить наши данные. Основная идея алгоритма заключается в том, что нам хотелось бы, чтобы наши наблюдения кластеризовались в группы на основе того, как они «общаются», или насколько они похожи друг на друга.
Заведём для этого какую-нибудь метрику «похожести», определяющуюся тем, что 
s(x_i, x_k)$» data-tex=»inline»/> если наблюдение 
больше похоже на наблюдение 
, чем на 
. Простым примером такой похожести будет отрицательный квадрат расстояния 
.
Теперь опишем сам процесс «общения». Для этого заведём две матрицы, инициализируемые нулями, одна из которых 
будет описывать, насколько хорошо -тое наблюдение подходит для того, чтобы быть «примером для подражания» для -того наблюдения относительно всех остальных потенциальных «примеров», а вторая — 
будет описывать, насколько правильным было бы для -того наблюдения выбрать -тое в качестве такого «примера». Звучит немного запутанно, но чуть дальше увидим пример «на пальцах».
После этого данные матрицы обновляются по очереди по правилам:
Спектральная кластеризация
Спектральная кластеризация объединяет несколько описанных выше подходов, чтобы получить максимальное количество профита от сложных многообразий размерности меньшей исходного пространства.
Для работы этого алгоритма нам потребуется определить матрицу похожести наблюдений (adjacency matrix). Можно это сделать таким же образом, как и для Affinity Propagation выше: 
. Эта матрица также описывает полный граф с вершинами в наших наблюдениях и рёбрами между каждой парой наблюдений с весом, соответствующим степени похожести этих вершин. Для нашей выше выбранной метрики и точек, лежащих на плоскости, эта штука будет интуитивной и простой — две точки более похожи, если ребро между ними короче. Теперь нам бы хотелось разделить наш получившийся граф на две части так, чтобы получившиеся точки в двух графах были в общем больше похожи на другие точки внутри получившейся «своей» половины графа, чем на точки в «другой» половине. Формальное название такой задачи называется Normalized cuts problem и подробнее про это можно почитать тут.
Агломеративная кластеризация
Наверное самый простой и понятный алгоритм кластеризации без фиксированного числа кластеров — агломеративная кластеризация. Интуиция у алгоритма очень простая:
Сам процесс поиска ближайших кластеров может происходить с использованием разных методов объединения точек:
Профит первых трёх подходов по сравнению с четвёртым в том, что для них не нужно будет пересчитывать расстояния каждый раз после склеивания, что сильно снижает вычислительную сложность алгоритма.
По итогам выполнения такого алгоритма можно также построить замечательное дерево склеивания кластеров и глядя на него определить, на каком этапе нам было бы оптимальнее всего остановить алгоритм. Либо воспользоваться тем же правилом локтя, что и в k-means.
К счастью для нас в питоне уже есть замечательные инструменты для построения таких дендрограмм для агломеративной кластеризации. Рассмотрим на примере наших кластеров из K-means:
Метрики качества кластеризации
Задача оценки качества кластеризации является более сложной по сравнению с оценкой качества классификации. Во-первых, такие оценки не должны зависеть от самих значений меток, а только от самого разбиения выборки. Во-вторых, не всегда известны истинные метки объектов, поэтому также нужны оценки, позволяющие оценить качество кластеризации, используя только неразмеченную выборку.
Выделяют внешние и внутренние метрики качества. Внешние используют информацию об истинном разбиении на кластеры, в то время как внутренние метрики не используют никакой внешней информации и оценивают качество кластеризации, основываясь только на наборе данных. Оптимальное число кластеров обычно определяют с использованием внутренних метрик.
Adjusted Rand Index (ARI)
Предполагается, что известны истинные метки объектов. Данная мера не зависит от самих значений меток, а только от разбиения выборки на кластеры. Пусть — число объектов в выборке. Обозначим через 
— число пар объектов, имеющих одинаковые метки и находящихся в одном кластере, через 
— число пар объектов, имеющих различные метки и находящихся в разных кластерах. Тогда Rand Index это
То есть это доля объектов, для которых эти разбиения (исходное и полученное в результате кластеризации) «согласованы». Rand Index (RI) выражает схожесть двух разных кластеризаций одной и той же выборки. Чтобы этот индекс давал значения близкие к нулю для случайных кластеризаций при любом и числе кластеров, необходимо нормировать его. Так определяется Adjusted Rand Index:
Эта мера симметрична, не зависит от значений и перестановок меток. Таким образом, данный индекс является мерой расстояния между различными разбиениями выборки. 
принимает значения в диапазоне 
. Отрицательные значения соответствуют «независимым» разбиениям на кластеры, значения, близкие к нулю, — случайным разбиениям, и положительные значения говорят о том, что два разбиения схожи (совпадают при 
).
Adjusted Mutual Information (AMI)
Данная мера очень похожа на . Она также симметрична, не зависит от значений и перестановок меток. Определяется с использованием функции энтропии, интерпретируя разбиения выборки, как дискретные распределения (вероятность отнесения к кластеру равна доле объектов в нём). Индекс 
определяется как взаимная информация для двух распределений, соответствующих разбиениям выборки на кластеры. Интуитивно, взаимная информация измеряет долю информации, общей для обоих разбиений: насколько информация об одном из них уменьшает неопределенность относительно другого.
Аналогично определяется индекс 
, позволяющий избавиться от роста индекса с увеличением числа классов. Он принимает значения в диапазоне 
. Значения, близкие к нулю, говорят о независимости разбиений, а близкие к единице – об их схожести (совпадении при 
).
Гомогенность, полнота, V-мера
Формально данные меры также определяются с использованием функций энтропии и условной энтропии, рассматривая разбиения выборки как дискретные распределения:
здесь — результат кластеризации, — истинное разбиение выборки на классы. Таким образом, 
измеряет, насколько каждый кластер состоит из объектов одного класса, а 
— насколько объекты одного класса относятся к одному кластеру. Эти меры не являются симметричными. Обе величины принимают значения в диапазоне , и большие значения соответствуют более точной кластеризации. Эти меры не являются нормализованными, как или , и поэтому зависят от числа кластеров. Случайная кластеризация не будет давать нулевые показатели при большом числе классов и малом числе объектов. В этих случаях предпочтительнее использовать . Однако при числе объектов более 1000 и числе кластеров менее 10 данная проблема не так явно выражена и может быть проигнорирована.
Для учёта обеих величин и одновременно вводится 
-мера, как их среднее гармоническое:
Она является симметричной и показывает, насколько две кластеризации схожи между собой.
Силуэт
В отличие от описанных выше метрик, данный коэффициент не предполагает знания истинных меток объектов, и позволяет оценить качество кластеризации, используя только саму (неразмеченную) выборку и результат кластеризации. Сначала силуэт определяется отдельно для каждого объекта. Обозначим через — среднее расстояние от данного объекта до объектов из того же кластера, через — среднее расстояние от данного объекта до объектов из ближайшего кластера (отличного от того, в котором лежит сам объект). Тогда силуэтом данного объекта называется величина:
С помощью силуэта можно выбирать оптимальное число кластеров (если оно заранее неизвестно) — выбирается число кластеров, максимизирующее значение силуэта. В отличие от предыдущих метрик, силуэт зависит от формы кластеров, и достигает больших значений на более выпуклых кластерах, получаемых с помощью алгоритмов, основанных на восстановлении плотности распределения.
И напоследок давайте посмотрим на эти метрики для наших алгоритмов, запущенных на данных рукописных цифр MNIST:
| ARI | AMI | Homogenity | Completeness | V-measure | Silhouette | |
|---|---|---|---|---|---|---|
| K-means | 0.662295 | 0.732799 | 0.735448 | 0.742972 | 0.739191 | 0.182097 |
| Affinity | 0.175174 | 0.451249 | 0.958907 | 0.486901 | 0.645857 | 0.115197 |
| Spectral | 0.752639 | 0.827818 | 0.829544 | 0.876367 | 0.852313 | 0.182195 |
| Agglomerative | 0.794003 | 0.856085 | 0.857513 | 0.879096 | 0.868170 | 0.178497 |
3. Домашнее задание
Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.
В демо-версии домашнего задания предлагается поработать с данными Samsung по распознаванию видов активностей людей. Задача интересная, мы на нее посмотрим и как на задачу кластеризации (забыв, что выборка размечена) и как на задачу классификации. Jupyter-заготовка, веб-форма для ответов, там же найдете и решение.
4. Полезные источники
Статья написана в соавторстве с yorko (Юрием Кашницким). Материал статьи доступен в виде тетрадки Jupyter в GitHub-репозитории курса.