такая модель как дерево работ обычно используется для каких проектов

Плюсы и минусы дерева решений

— Формирует четкие и понятные правила классификации. То есть деревья решений хорошо и быстро интерпретируются

— Деревья способны генерировать правила в областях, где специалисту трудно формализовать свои знания

— Они легко визуализируются, то есть могут «интерпретироваться» не только как модель в целом, но и как прогноз для отдельного тестового субъекта (путь в дереве)

— Быстро обучаются и прогнозируют

— Не требуется много параметров модели

— Поддерживают как числовые, так и категориальные признаки

— Быстро приводят к результату и решению проблемы

— Деревья решений очень чувствительны. Небольшие изменения обучающей выборки могут привести к глобальным корректировкам модели.

— Разделяющая граница имеет определенные ограничения, из-за чего дерево решений по качеству классификации уступает другим методам.

— Возможно переобучение дерева решений, из-за чего приходится прибегать к методу «отсечения ветвей», установке минимального числа элементов в листьях дерева или максимальной глубины дерева (то есть ограниченность модели)

— Сложный поиск оптимального дерева решений

— Нет 100-процентной гарантии нахождения оптимального дерева

Читайте и другие статьи из раздела Лайфхаки на invme:

Источник

Такая модель как дерево работ обычно используется для каких проектов

2. методы структуризации проектов

Для структуризации проекта используют ряд специальных моделей:

• организационную структуру исполнителей;

• структуру потребляемых ресурсов;

При этом методы структуризации проекта принципиально сводятся к двум [21, 22, 26]:

• «сверху-вниз» – определяются общие задачи, на основе которых далее осуществляется детализация уровней проекта;

• «снизу-вверх» – определяются частные задачи, а затем происходит их обобщение.

Дерево целей – это графы, схемы, показывающие, как генеральная цель проекта разбивается на подцели следующего уровня и т. д. (дерево –это связанный граф, выражающий соподчинение и взаимосвязи элементов. В данном случае такими элементами являются цели и подцели).

Представление целей начинается с верхнего уровня, дальше они последовательно разукрупняются. При этом основным правилом разукрупнения целей является полнота: каждая цель верхнего уровня должна быть представлена исчерпывающим образом в виде подцелей следующего уровня.

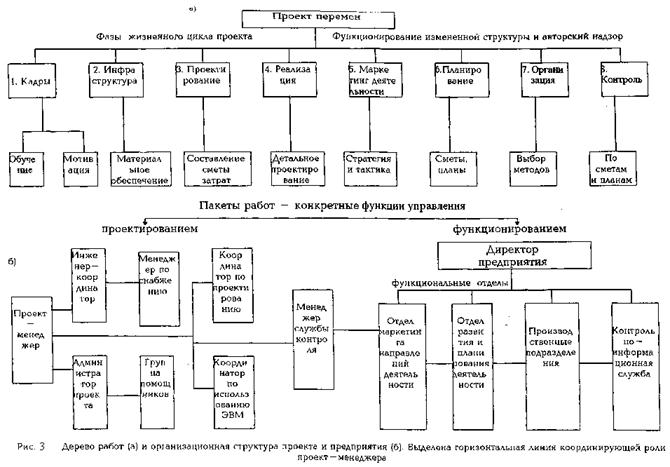
Пример формирования дерева целей представлен на рис. 3.1.

Рис. 3.1. Пример формирования дерева целей

Дерево решений – граф, схема, отражающие структуру задачи оптимизации многошагового процесса [23]. Ветви дерева отображают различные события, которые могут иметь место, а узлы (вершины) – точки, в которых возникает необходимость выбора. Причем узлы различны: в одних выбор осуществляет сам проект-менеджер из некоторого набора альтернатив, в других – выбор от него не зависит. В таких случаях проект-менеджер может осуществлять оценку вероятности того или иного ее «решения». Пример формирования дерева решений представлен на рис. 3.2.

Дерево работ (WBS – Work Breakdown Structure) – иерархическая структура, отражающая последовательность декомпозиции проекта на подпроекты, пакеты работ различного уровня, пакеты детальных работ [23]. Дерево работ является основой для формирования системы управления проекта, то есть предоставляет полную информацию для дальнейшей оптимизации последовательности выполнения работ, их анализа и контроля, назначения ответственных за выполнение тех или иных работ.

Нижний уровень дерева соответствует пакетам работ. Это последние элементы подразделов, за которые ответственны подрядчик или соответствующий отдел организации-заказчика. Пакет работ не следует отделять от других работ проекта, но связи этого пакета с остальной частью проекта должны быть четкими. Эти связи не следует усложнять настолько, чтобы затруднялась координация.

Пакет работ является также самостоятельной финансовой единицей,

Рис. 3.2. Пример формирования дерева решений

должен иметь отдельную смету, бюджет и отчет о расходах. Вычленение пакетов работ представляет большое удобство при разработке сетевого графика проекта. Намного легче планировать отдельные пакеты и затем формировать сетевой график проектов из фрагментов, нежели разрабатывать сетевой график в целом без дерева работ проекта.

На основе WBS формируется структурная схема административного управления проектом. Таким образом, разделение проекта на пакеты работ удовлетворяет двум задачам: планирования и оперативного управления. Поэтому одновременно с WBS необходимо развивать организационно-административное дерево и увязывать его структурные единицы с пакетами работ.

Декомпозиция работ может осуществляться по:

– компонентам товара, услуги и т. д., получаемым в результате реализации проекта;

– процессным или функциональным элементам деятельности организации, реализующей проект;

– этапам жизненного цикла проекта и т. д.

Зачастую на практике используются комбинированные структуры, построенные с использованием нескольких оснований декомпозиции.

Для обеспечения эффективного управления проектом при разработке плана необходимо:

– учесть в плане все разделы, этапы и работы проекта;

– учесть в плане все организации, участвующие в проекте;

– обеспечить действенность управления путем распределения ответственности.

Первое требование может быть удовлетворено разбивкой проекта на пакеты работ с помощью WBS. Для выполнения последних двух требований необходимо определить, какая организация ответственна за каждый пакет или уровень дерева работ, то есть необходимо четко определить уровни и объемы ответственности в организационной структуре.

Пример формирования дерева работ представлен на рис. 3.3.

Организационная структура проекта (OBS – Organisation Breakdown Structure) и матрица ответственности являются основой для создания команды проекта.

В схеме организационной структуры руководитель проекта находится на верхнем уровне, а на более низких уровнях последовательно располагаются отделы или организации функционального управления работами. Эти уровни иногда соответствуют уровням WBS. Например, отдел маркетинга будет ответственным за пакет работ «Маркетинговые исследования».

Цель OBS состоит в указании не только исполнителей работ для каждого пакета, но и в определении отделов, организаций, ответственных за выполнение соответствующих работ.

На практике связь между пакетами работ и элементами организационной структуры достаточно размыта, но вместе с тем должны быть четко оговорены права и обязанности участников проекта.

Матрица ответственности связывает пакеты работ с организациями-исполнителями на основе WBS и OBS. В матрице определяются основные исполнители по пакетам работ. Элементами матрицы являются коды видов деятельности или стоимость работ. Количество видов ответственности может быть различным в зависимости от содержания проекта. На рис. 3.4. представлен пример формирования матрицы ответственности.

Рис. 3.3. Пример структуризации работ проекта по реконструкции завода

Рис. 3.4. Пример формирования матрицы ответственности [22, c. 438]

На основе проделанных шагов строится так называемая матрица распределения ответственности. Матрица приписывает каждому пакету работ конкретных исполнителей.

Искусство декомпозиции состоит в умелом согласовании структур проекта, к которым относятся организационная структура, структура статей затрат (ABS – Account Breakdown Structure), структура ресурсов (RBS – Resource Breakdown Structure) и другие.

Сетевые модели. По мере продвижения работы над проектом создаются деревья WBS и OBS, то есть выделяются пакеты работ с назначенными для них исполнителями, что дает возможность подготавливать сетевой график узловых событий. Наконец, становится возможным разработать детальные сетевые графики, соответствующие узловым событиям и целям. Поскольку эти сетевые графики представляют не проект в целом, а его отдельные пакеты работ, они называются сетевыми блоками или подсетями. Если работа по нескольким взаимозависимым пакетам осуществляется одновременно, причем для каждого из них требуется разработать отдельное расписание, то каждый пакет представляется отдельной подсетью.

Подсеть может составлять часть сетевого графика либо быть автономной. Расчленение сетевого графика на подсети позволяет персоналу, ответственному за проект, концентрироваться на своих собственных работах. Каждый руководитель на своем уровне может вести работу независимо от других в соответствии со своей подсетью, что освобождает его от необходимости иметь дело с полным сетевым графиком. Для руководства разделение проекта на подсети обеспечивает возможность эффективного контроля. Оно может в целях экономии времени уделять больше внимания управлению наиболее важными (критическими) подсетями, вместо того чтобы постоянно контролировать весь сетевой график. Таким образом, структура, выявленная при создании WBS, OBS и сетевого графика узловых событий, сохраняется и при разработке подсетей. Важное значение при разработке подсети имеет планирование операций в пределах совокупности узловых событий.

Структура потребляемых ресурсов. Для анализа средств, которые необходимы для достижения целей и подцелей проекта, осуществляется структуризация ресурсов различных типов. Иерархически построенный граф фиксирует необходимые на каждом уровне ресурсы для реализации проекта. Например, на первом уровне определяются материально-технические, трудовые и финансовые ресурсы. Затем материально-технические ресурсы дифференцируются на строительные материалы, машины, оборудование. Строительные материалы – на складируемые и не складируемые и т. д.

Контрольные вопросы к третьей теме

1. Что такое структуризация? Для чего она необходима?

2. Что включает в себя процесс структуризации?

Что такое дерево целей? Кто его разрабатывает? Каково назначение?

Что такое дерево решений? Кто его разрабатывает? Каково назначение?

Что такое дерево работ? Кто его разрабатывает? Каково назначение?

Как взаимосвязана структура работ и организационная структура?

Какая информация отображается в матрице ответственности?

Упражнения к третьей теме

1. Сформируйте дерево целей для проекта, выбранного в п. 7 второй темы.

2. Сформируйте дерево решений для проекта, выбранного в п. 7 второй темы.

3. Сформируйте дерево работ для проекта, выбранного в п. 7 второй темы.

4. Разработайте организационную структуру для выбранного проекта.

5. Разработайте затратную структуру проекта.

6. Сформируйте интегрированную схему рабочей, затратной и организационной структур проекта.

7. Разработайте матрицу ответственности для проекта.

8. Разработайте календарный план реализации проекта.

Источник

Что такое дерево решений и где его используют?

Ребята, привет! Сегодня команда ProductStar подготовила для вас статью, в которой мы рассмотрели общие принципы работы и области применения дерева решений. Материал подготовлен на основе работы Акобира Шахиди «Деревья решений: общие принципы»

Дерево решений — метод автоматического анализа больших массивов данных. В этой статье рассмотрим общие принципы работы и области применения.

Дерево решений — эффективный инструмент интеллектуального анализа данных и предсказательной аналитики. Он помогает в решении задач по классификации и регрессии.

В отличие от нейронных сетей, деревья как аналитические модели проще, потому что правила генерируются на естественном языке: например, «Если реклама привела 1000 клиентов, то она настроена хорошо».

Правила генерируются за счет обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область. Поэтому их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.

В обучающем множестве для примеров должно быть задано целевое значение, так как деревья решений — модели, создаваемые на основе обучения с учителем. По типу переменной выделяют два типа деревьев:

дерево классификации — когда целевая переменная дискретная;

дерево регрессии — когда целевая переменная непрерывная.

Развитие инструмента началось в 1950-х годах. Тогда были предложены основные идеи в области исследований моделирования человеческого поведения с помощью компьютерных систем.

Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с Джоном Р. Куинленом (автором алгоритма ID3 и последующих модификаций С4.5 и С5.0) и Лео Брейманом, предложившим алгоритм CART и метод случайного леса.

Структура дерева решений

Рассмотрим понятие более подробно. Дерево решений — метод представления решающих правил в определенной иерархии, включающей в себя элементы двух типов — узлов (node) и листьев (leaf). Узлы включают в себя решающие правила и производят проверку примеров на соответствие выбранного атрибута обучающего множества.

Простой случай: примеры попадают в узел, проходят проверку и разбиваются на два подмножества:

первое — те, которые удовлетворяют установленное правило;

второе — те, которые не удовлетворяют установленное правило.

Далее к каждому подмножеству снова применяется правило, процедура повторяется. Это продолжается, пока не будет достигнуто условие остановки алгоритма. Последний узел, когда не осуществляется проверка и разбиение, становится листом.

Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной. В листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается этим листом.

Пример попадает в лист, если соответствует всем правилам на пути к нему. К каждому листу есть только один путь. Таким образом, пример может попасть только в один лист, что обеспечивает единственность решения.

Терминология

Изучите основные понятия, которые используются в теории деревьев решений, чтобы в дальнейшем было проще усваивать новый материал.

Какие задачи решает дерево решений?

Его применяют для поддержки процессов принятия управленческих решений, используемых в статистистике, анализе данных и машинном обучении. Инструмент помогает решать следующие задачи:

Классификация. Отнесение объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные задачи.

Регрессия (численное предсказание). Предсказание числового значения независимой переменной для заданного входного вектора.

Описание объектов. Набор правил в дереве решений позволяет компактно описывать объекты. Поэтому вместо сложных структур, используемых для описания объектов, можно хранить деревья решений.

Процесс построения дерева решений

Основная задача при построении дерева решений — последовательно и рекурсивно разбить обучающее множество на подмножества с применением решающих правил в узлах. Но как долго надо разбивать? Этот процесс продолжают до того, пока все узлы в конце ветвей не станут листами.

Узел становится листом в двух случаях:

естественным образом — когда он содержит единственный объект или объект только одного класса;

после достижения заданного условия остановки алгоритм — например, минимально допустимое число примеров в узле или максимальная глубина дерева.

В основе построения лежат «жадные» алгоритмы, допускающие локально-оптимальные решения на каждом шаге (разбиения в узлах), которые приводят к оптимальному итоговому решению. То есть при выборе одного атрибута и произведении разбиения по нему на подмножества, алгоритм не может вернуться назад и выбрать другой атрибут, даже если это даст лучшее итоговое разбиение. Следовательно, на этапе построения дерева решений нельзя точно утверждать, что удастся добиться оптимального разбиения.

Популярные алгоритмы, используемых для обучения деревьев решений, строятся на базе принципа «разделяй и властвуй». Задают общее множество S, содержащее:

n примеров, для каждого из которых задана метка класса Ci(i = 1..k);

m атрибутов Aj(j = 1..m), которые определяют принадлежность объекта к тому или иному классу.

Тогда возможно три случая:

Примеры множества S имеют одинаковую метку Ci, следовательно, все обучающие примеры относятся к одному классу. В таком случае обучение не имеет смысла, потому что все примеры в модели будут одного класса, который и «научится» распознавать модель. Само дерево будет похоже на один большой лист, ассоциированный с классом Ci. Тогда его использование не будет иметь смысла, потому что все новые объекты будут относиться к одному классу.

Множество S — пустое множество без примеров. Для него сформируется лист, класс которого выберется из другого множества. Например, самый распространенный из родительского множества класс.

Множество S состоит из обучающих примеров всех классов Ck. В таком случае множество разбивается на подмножества в соответствии с классами. Для этого выбирают один из атрибутов Aj множества S, состоящий из двух и более уникальных значений: a1, a2, …, ap), где p — число уникальных значений признака. Множество S разбивают на p подмножеств (S1, S2, …, Sp), состоящих из примеров с соответствующим значением атрибута. Процесс разбиения продолжается, но уже со следующим атрибутом. Он будет повторяться, пока все примеры в результирующих подмножества не окажутся одного класса.

Третья применяется в большинстве алгоритмов, используемых для построения деревьев решений. Эта методика формирует дерево сверху вниз, то есть от корневого узла к листьям.

Сегодня существует много алгоритмов обучения: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и другие. Самыми популярными считаются:

ID3 (Iterative Dichotomizer 3). Алгоритм позволяет работать только с дискретной целевой переменной. Деревья решений, построенные на основе ID3, получаются квалифицирующими. Число потомков в узле неограниченно. Алгоритм не работает с пропущенными данными.

C4.5. «Продвинутая» версия ID3, дополненная возможностью работы с пропущенными значениями атрибутов. В 2008 году издание Spring Science провело исследование и выявило, что C4.5 — самый популярный алгоритм Data Mining.

CART (Classification and Regression Tree). Алгоритм решает задачи классификации и регрессии, так как позволяет использовать дискретную и непрерывную целевые переменные. CART строит деревья, в каждом узле которых только два потомка.

Основные этапы построения дерева решений

Построение осуществляется в 4 этапа:

Выбрать атрибут для осуществления разбиения в данном узле.

Определить критерий остановки обучения.

Выбрать метод отсечения ветвей.

Оценить точность построенного дерева.

Далее рассмотрим каждый подробнее.

Выбор атрибута разбиения

Разбиение должно осуществляться по определенному правилу, для которого и выбирают атрибут. Причем выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса или были максимально приближены к этому. Иными словами — количество объектов из других классов в каждом из этих множеств должно быть как можно меньше.

Критериев существует много, но наибольшей популярностью пользуются теоретико-информационный и статистический.

Теоретико-информационный критерий

В основе критерия лежит информационная энтропия:

где n — число классов в исходном подмножестве, Ni — число примеров i-го класса, N — общее число примеров в подмножестве.

Энтропия рассматривается как мера неоднородности подмножества по представленным в нем классам. И даже если классы представлены в равных долях, а неопределенность классификации наибольшая, то энтропия тоже максимальная. Логарифм от единицы будет обращать энтропию в ноль, если все примеры узла относятся к одному классу.

Если выбранный атрибут разбиения Aj обеспечивает максимальное снижение энтропии результирующего подмножества относительно родительского, его можно считать наилучшим.

Но на деле об энтропии говорят редко. Специалисты уделяют внимание обратной величине — информации. В таком случае лучшим атрибутом будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:

где Info(S) — информация, связанная с подмножеством S до разбиения, Info(Sa) — информация, связанная с подмножеством, полученным при разбиении атрибута A.

Задача выбора атрибута в такой ситуации заключается в максимизации величины Gain(A), которую называют приростом информации. Поэтому теоретико-информационный подход также известен под название «критерий прироста информации.

Статистический подход

В основе этого метода лежит использования индекса Джини. Он показывает, как часто случайно выбранный пример обучающего множества будет распознан неправильно. Важное условие — целевые значения должны браться из определенного статистического распределения.

Если говорить проще, то индекс Джини показывает расстояние между распределениями целевых значений и предсказаниями модели. Минимальное значение показателя говорит о хорошей работе модели.

Индекс Джини рассчитывается по формуле:

где Q — результирующее множество, n — число классов в нем, pi — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса).

Значение показателя меняется от 0 до 1. Если индекс равен 0, значит, все примеры результирующего множества относятся к одному классу. Если равен 1, значит, классы представлены в равных пропорциях и равновероятны. Оптимальным считают то разбиение, для которого значение индекса Джини минимально.

Критерий остановки алгоритма

Алгоритм обучения может работать до получения «чистых» подмножеств с примерами одного класса. В таком случае высока вероятность получить дерево, в котором для каждого примера будет создан отдельный лист. Такое дерево не получится применять на практике из-за переобученности. Каждому примеру будет соответствовать свой уникальный путь в дереве. Получится набор правил, актуальный только для данного примера.

Переобучение в случае дерева решений имеет схожие с нейронными сетями последствия. Оно будет точно распознавать примеры из обучения, но не сможет работать с новыми данными. Еще один минус — структура переобученного дерева сложна и плохо поддается интерпретации.

Специалисты решили принудительно останавливать строительство дерева, чтобы оно не становилось «переобученным».

Для этого используют несколько подходов:

Ранняя остановка. Алгоритм останавливается после достижения заданного значения критерия (например, процентной доли правильно распознанных примеров). Преимущество метода — сокращение временных затрат на обучение. Главный недостаток — ранняя остановка негативно сказывается на точности дерева. Из-за этого многие специалисты советуют отдавать предпочтение отсечению ветей.

Ограничение глубины дерева. Алгоритм останавливается после достижения установленного числа разбиений в ветвях. Этот подход также негативно сказывается на точности дерева.

Задание минимально допустимого числа примеров в узле. Устанавливается ограничение на создание узлов с числом примером меньше заданного (например, 7). В таком случае не будут создаваться тривиальные разбиения и малозначимые правила.

Этими подходами пользуются редко, потому что они не гарантируют лучшего результата. Чаще всего, они работают только в каких-то определенных случаях. Рекомендаций по использованию какого-либо метода нет, поэтому аналитикам приходится набирать практический опыт путем проб и ошибок.

Отсечение ветвей

Без ограничения «роста» дерево решений станет слишком большим и сложным, что сделает невозможной дальнейшую интерпретацию. А если делать решающие правила для создания узлов, в которые будут попадать по 2-3 примера, они не лишатся практической ценности.

Поэтому многие специалисты отдают предпочтение альтернативному варианту — построить все возможные деревья, а потом выбрать те, которые при разумной глубине обеспечивают приемлемый уровень ошибки распознавания. Основная задача в такой ситуации — поиск наиболее выгодного баланса между сложностью и точностью дерева.

Но и тут есть проблема: такая задача относится к классу NP-полных задач, а они, как известно, эффективных решений не имеют. Поэтому прибегают к методу отсечения ветвей, который реализуется в 3 шага:

Строительство полного дерева, в котором листья содержат примеры одного класса.

Определение двух показателей: относительную точность модели (отношение числа правильно распознанных примеров к общему числу примеров) и абсолютную ошибку (число неправильно классифицированных примеров).

Удаление листов и узлов, потеря которых минимально скажется на точности модели и увеличении ошибки.

Отсечение ветвей проводят противоположно росту дерева, то есть снизу вверх, путем последовательного преобразования узлов в листья.

Главное отличие метода «отсечение ветвей» от преждевременной остановки — получается найти оптимальное соотношение между точностью и понятностью. При этом уходит больше времени на обучение, потому что в рамках этого подхода изначально строится полное дерево.

Извлечение правил

Иногда упрощения дерева недостаточно, чтобы оно легко воспринималось и интерпретировалось. Тогда специалисты извлекают из дерева решающие правила и составляют из них наборы, описывающие классы.

Для извлечения правил нужно отслеживать все пути от корневого узла к листьям дерева. Каждый путь дает правило с множеством условий, представляющих собой проверку в каждом узле пути.

Если представить сложное дерево решений в виде решающих правил (вместо иерархической структуры узлов), оно будет проще восприниматься и интерпретироваться.

Преимущества и недостатки дерева решений

Преимущества:

Формируют четкие и понятные правила классификации. Например, «если возраст

Источник