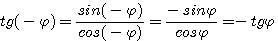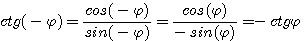тангенс какая функция четная или нечетная
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №2 Чётность и нечётность тригонометрических функций. Периодичность.
Перечень вопросов, рассматриваемых в теме
Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x).
Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.
Область. определения функции (D) — множество R всех действительных чисел
Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.
Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная
Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.
Область определения функции (D) — множество R всех действительных чисел.
Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.
Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная


Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Выясним, является ли функция
чётной или нечётной?
Пример 2. Доказать, что число 2π является наименьшим положительным периодом функции y=cos x
Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π
Доклад «Четность, нечетность, периодичность тригонометрических функций»
Ищем педагогов в команду «Инфоурок»
Четность, нечетность, периодичность тригонометрических функций
Четная функция – это Функция y = f ( x ) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f (- x ) = f ( x ) Свойства: симметричен относительно оси координат.
Практическое задание: как определить четная функция или не четная?
Рассмотрим следующий рисунок (рис. 1):
Периодичность тригонометрических функций
Практическое задание: как узнать является ли функция периодичной?
Рассмотрим рисунок (2)
Примеры задач на использование четности, нечетности и периодичности тригонометрических функций
Является ли функция y =2+ sin ^2 x
y(-x) =2+sin^2(-x) =2+(-sin x) ^2 = 2+sin^2 x=y(x)>
Доказать, что f(x) = Sin 3x – периодическая функция с периодом (2 π) /3.
Данная функция определена для всех x є R, поэтому достаточно показать, что для любого x верно равенство f (x + T) = f(x).
f(x + (2 π )/3) = Sin 3(x + (2 π )/3) = Sin (3x + 2 π ) = Sin 3x = f(x)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-1517110
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Школьников не планируют переводить на удаленку после каникул
Время чтения: 1 минута
Минпросвещения планирует прекратить прием в колледжи по 43 профессиям
Время чтения: 1 минута
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников
Время чтения: 1 минута
Минобразования Кузбасса рекомендовало техникумам и школам уйти на каникулы до 7 ноября
Время чтения: 1 минута
В Хабаровске утвердили дополнительные школьные каникулы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Универсальная технологическая карта урока «Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций» по учебнику А.Г. Мерзляк и др. «Алгебра и начала математического анализа. Базовый уровень»
Ищем педагогов в команду «Инфоурок»
Универсальная технологическая карта урока
Алгебра и начала математического анализа
Знаки значений тригонометрических функций.
Четность и нечетность тригонометрических функций.
Педагогические цели урока
1. Образовательные: систематизировать изученный теоретический материал по определениям синуса, косинуса, тангенса угла; выяснить какие знаки имеют синус, косинус и тангенс в различных четвертях; проверить степень усвоения знаний по данной теме. Научиться выяснять какой является функция: четной или нечетной.
2. Развивающие: развивать и совершенствовать умения применять имеющиеся знания в различных ситуациях; развивать внимание, память; развивать математическую речь; развивать умение классифицировать и устанавливать взаимосвязи, формировать умение работать самостоятельно.
3. Воспитательные: воспитывать у учащихся аккуратность в оформлении заданий в тетради и на доске; воспитывать культуру общения и поведения; воспитывать логически мыслящую личность, умение осуществлять самоконтроль.
Обучение нахождению знаков значений синуса, косинуса, тангенса числа; определению четности и нечетности, развитие умений самостоятельно ставить цель деятельности и контролировать свою деятельность.
Урок открытия нового знания
Планируемые образовательные результаты (с учетом разделов «Ученик научится», «Ученик получит возможность научиться»)
Находить знаки значений тригонометрических функций.
Исследовать тригонометрические функции на четность и нечетность.
Регулятивные: формировать умения самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.
Познавательные: выстраивать логические рассуждения, делать умозаключения и собственные выводы.
Коммуникативные: владеть и осознанно применять речевые средства в зависимости от ситуации и задачи коммуникации. Поддерживать беседу, уметь выслушивать собеседника и доходчиво донести до него свои мысли и доводы.
Формировать независимость суждений
Условия реализации урока
Информационные ресурсы (в том числе ЦОР и Интернет)
Методические ресурсы (методическая литература, стратегическая технология и тактические технологии
А.Г. Мерзляк, Д.А. Номировский,
В.Б. Полонский, М.С. Якир
«Алгебра и начала математического анализа». Учебник. 10 класс. Базовый уровень.
.Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский, М.С.Якир
«Алгебра и начала математического анализа». Методическое пособие. 10 класс. Базовый уровень.
Урок открытия нового.
Организационный момент. Этап урока (название, время, цель). Количество этапов зависит от типа урока.
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
Приветствует учащихся, положительный настрой на урок
Приветствуют учителя, проверяют готовность к уроку
Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Этап урока (название, время, цель)
Учитель создает условия для возникновения внутренней потребности включения в деятельность («хочу»);
актуализирует требования к ученику со стороны учебной деятельности («надо»);
устанавливает тематические рамки учебной деятельности («могу»).
Через повторение ранее изученного материала подвести к восприятию новой темы.
«В математике есть своя красота, как в живописи и поэзии.»
«Первое условие, которое надлежит выполнять в математике, это быть точным, второе- быть ясным и, насколько можно, простым.»
Прежде чем приступить к изучению нового материала, повторим пройденный.
1.Сравните с нулем координаты точки А (х;у ), если эта точка лежит:
1) в I координатной четверти
2) во II координатной четверти
3) в III координатной четверти
4) в IV координатной четверти
2.Четной или нечетной является функция
3.Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
1.Представляют прямоугольную систему координат, мысленно располагают в ней точку и отвечают:
3.Учащиеся активно поднимают руки и отвечают на вопрос учителя.
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Формулируют тему. «Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций».
Самоопределение; целеполагание, планирование учебного сотрудничества с учителем и сверстниками.
Развитие умения по применению нового знания. Этап урока (название, время, цель)
Пусть точка Р получена в результате поворота точки Р0 ( 1 ; 0) вокруг начала координат на угол α.
Знаки значений синуса и косинуса схематически показаны на рисунке.
Пусть точки Р1 и Р2 получены в результате поворота точки Р0 (1 ; 0) на углы α и – α соответственно.
Для любого α точки Р1 и Р2 имеют равные абсциссы и противоположные ординаты.
Тогда для любого действительного числа α
Функции тангенс и котангенс – нечетные.
Воспроизвели и зафиксировали знания, умения и навыки, достаточные для построения нового способа действий,
Активизировали соответствующие мыслительные операции (анализ, синтез, сравнение, обобщение и т.д.) и познавательные процессы (внимание, память и т.д.);
Синус, косинус считая,
Алгоритм не забываем:
Четверть – знак – название.
Самостоятельное выделение и формулирование познавательной цели.
Планирование учебного сотрудничества с учителем и сверстниками.
Физкультминутка. Этап урока (название, время, цель)
Встанем, глубоко вздохнем.
Руки в стороны, вперед,
Влево, вправо поворот.
Раз – наклон и прямо встать
Руки вниз и вверх поднять.
Руки плавно опустили,
Всем улыбки подарили.
Стоя, выполняют упражнения.
Создание благоприятного психологического климата.
Первичное усвоение и закрепление новых знаний
Анализирует причины затруднений и помогает в выборе знания, которого недостает.
№ 16.1. Углом какой четверти является угол:
Ответы : 1) I; 2) III; 3) III; 4) IV; 5) I; 6) II; 7) III;
Работаем в тетрадях:
Поскольку 110 0 является углом II четверти, то sin 110 0 > 0.
Поскольку 200 0 является углом III четверти, то cos 200 0
Далее работаем по вариантам с последующей самопроверкой.
I вариант – нечетные ; II вариант – четные номера.
№ 16.4. Найти значение выражения:
№16.6. Найти значение выражения:
Ответы: 1) (3 +√2)/2; 2) 2; 3) 4.
№ 16.16. Исследовать на четность функцию:
Далее I вариант: № 2 и 4, II вариант: № 3 и 5.
Ответы: 2) четная, 4) четная,
3), 5) ни четная, ни нечетная.
Попытались самостоятельно выполнить индивидуальное задание на применение нового знания.
Зафиксировали возникшее затруднение в выполнении пробного действия или его обосновании.
Когда стою по стойке смирно,
То очень я похож на синус,
А лягу отдохнуть, устав,
На косинус похожим стал.
Созданы условия для усвоения определения знака функции, исследования функции на четность.
Сформулировали конкретную цель своих будущих учебных действий.
Планирование учебного сотрудничества с учителем и сверстниками.
1.Когда говорят, что α является углом I четверти? II четверти? III четверти? IV четверти?
2. Какие знаки имеют синус, косинус, тангенс и котангенс в каждой из четвертей?
3. Какие из тригонометрических функций являются четными, а какие нечетными?
Домашнее задание: § 16, № 16.3., 16.5., 16.7., 16.17.
Достигли мы своих целей?
Что для вас оказалось самым сложным?
Оцените свою работу на уроке.
Рефлексия собственной деятельности.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Конспект урока по математике на тему «Задачи на движение по реке» (4 класс)
Конспект урока по математике «Доли»
Урок математики на тему «Умножение»
Устная работа на уроках математики
Нестандартные виды работы с задачами на уроке как средство реализации современных педагогических концепций и технологий
Урок математики в III классе Конспект урока и его самоанализ
Личностно-ориентированный подход в системе обучения математике
Технологическая карта урока по математике на тему «Окружность и круг» (5 класс)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5245750 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения планирует прекратить прием в колледжи по 43 профессиям
Время чтения: 1 минута
Почти все вузы в России открыли пункты вакцинации от ковида
Время чтения: 1 минута
Минобрнауки работает над изменением подходов к защите диплома
Время чтения: 1 минута
Школьников не планируют переводить на удаленку после каникул
Время чтения: 1 минута
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Более половины родителей не состоят в родительских чатах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Тангенс какая функция четная или нечетная
ЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
Четность тригонометрических функций.
Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки).
Поэтому конечные стороны OA 1 и ОА 2 этих углов симметричны относительно оси абсцисс.
Следовательно, синус является нечетной, а косинус — четной функцией угла.
Поэтому тангенс и котангенс являются нечетными функциями угла.
Выяснить, какие из данных функций являются четными и какие нечетными:
1) у = sin (—х); 4) у = sin x cos х; 7) у = sin 2 x;
2) у = cos (—х); 5) у = sec x; 8) у = cos 2 x;
3) у = tg (2х); 6) у = cosec x; 9) у = sin x + tg x.
Периодичность функций sin φ и cos φ
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.
Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.
Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.
Пусть f(х) есть некоторое выражение, зависящее от переменной величины х.
(Например, f(х) = x 2 , f(х) = sin x и т. д.)
Определяет у как функцию аргумента х.
Если при любых допустимых значениях аргумента х
где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.
Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.
При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.
Таким образом, cos φ = cos (φ + 360°n),
sin φ = sin (φ + 360°n), (1)
где n — любое целое число (положительное, отрицательное или нуль).
Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.
Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ
В частности, при φ = 0 получаем: sinТ = sin 0° = 0.
Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы
Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.
1. Доказать следующие соотношения:
а) sin 740° = sin 20°; в) cos 54° = cos (—1026°);
б) sin (—1000°) = sin 80°; г) cos (—1750°) = cos 50°.
2. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 360°:
a) sin 820°; б) cos (—7363°); в) sin (—600°).
3. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 180°:
a) cos 729°; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).
4. Доказать, что угол в 540° является одним из периодов функции у = cos2х.
5. Доказать, что угол и 360° является одним из периодов функции у = tgx.
6. Докажите, что любой период Т функции у = cos х является корнем уравнения
Верно ли обратное утверждение?
Периодичность функций tg φ и ctg φ
Следовательно, при любом φ
Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?
Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть
В частности, при φ = 0° получаем:
Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом (то есть наименьшим положительным периодом) функции tg φ является угол в 180°.
Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.
1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (—185°); в) ctg 300°; г) ctg (—210°).
2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90°:
3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.
4. Доказать, что любой период Т функции у = ctg х является корнем уравнения
Верно ли обратное утверждение?
О периодических функциях.
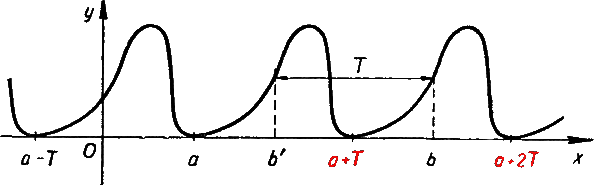
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.
Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.
Покажем, как можно определить значения этой функции в интервале ( а + Т, а + 2 T ).
Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.
В силу периодичности функции f(x)
Таким образом, по заданным значениям функции f
Итак, задание периодической с периодом Т функции f(x) на любом интервале длины Т дает возможность полностью охарактеризовать ее на всей числовой прямой. Поэтому для исследования функции f(x), периодической с периодом Т, достаточно изучить ее поведение лишь на каком-нибудь интервале длины Т. Например, для исследования функций у = sin φ и у = cos φ достаточно рассмотреть их лишь при 0° <φ <360°. Для исследования функции у = tg φ можно было бы ограничиться интервалом 0° <φ <180°. Но при φ = 90° tg φ не определен. Поэтому в данном случае целесообразнее выбрать какой-нибудь другой интервал, в каждой точке которою функция у = tg φ была бы определена. Мы отдадим предпочтение интервалу —90° < φ < 90°. Однако в принципе можно было бы выбрать, конечно, и интервал 0° <φ <180°. Для изучения функции сtg φ целесообразно выбрать интервал 0° < φ < 180°.
2. Может ли периодическая с периодом Т функция f(x) удовлетворить условию
Если может, то в каком случае? Ответ пояснить примерами.