тела вращения это какие фигуры
Тела вращения
Содержание
Примеры тел вращения
За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.
За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
Объём и площадь поверхности тел вращения
Объём и площадь поверхности тел вращения можно узнать при помощи теорем Гульдина-Паппа.
Площадь поверхности, образуемой при вращении линии, лежащей в плоскости целиком по одну сторону от оси вращения, равна произведению длины линии на длину окружности, пробегаемой центром масс этой линии.
Объём тела, образуемого при вращении фигуры, лежащей в плоскости целиком по одну сторону от оси вращения, равен произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры.
Литература
А.В. Погорелов. «Геометрия. 10-11 класс» §21.Тела вращения. — 2011
Примечания
Полезное
Смотреть что такое «Тела вращения» в других словарях:
деталь с закрытым уступом – тела вращения — Часть детали, поверхность которой ограничена с обеих сторон поверхностями вращения, имеющими больший диаметр. Наличие закрытых уступов не влияет на определение ступенчатости наружной поверхности. Проточки для выхода инструмента не считается… … Справочник технического переводчика
оболочка, имеющая форму тела вращения — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN shell of revolution … Справочник технического переводчика
тонкого тела теория — Обтекание тонкого тела при отличном от нуля угле атаки. тонкого тела теория теория пространственного безвихревого течения идеальной жидкости около тонких тел [тела, у которых поперечный размер l (толщина, размах) мал по сравнению с… … Энциклопедия «Авиация»
тонкого тела теория — Обтекание тонкого тела при отличном от нуля угле атаки. тонкого тела теория теория пространственного безвихревого течения идеальной жидкости около тонких тел [тела, у которых поперечный размер l (толщина, размах) мал по сравнению с… … Энциклопедия «Авиация»
Тонкого тела теория — теория пространственного безвихревого течения идеальной жидкости около тонких тел (тела, у которых поперечный размер l (толщина, размах) мал по сравнению с продольным размером L: (τ) = l/L … Энциклопедия техники
Частота вращения — Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки Уг … Википедия
ФИЗИКА ТВЕРДОГО ТЕЛА — раздел физики, изучающий структуру и свойства твердых тел. Научные данные о микроструктуре твердых веществ и о физических и химических свойствах составляющих их атомов необходимы для разработки новых материалов и технических устройств. Физика… … Энциклопедия Кольера
ПАДЕНИЕ ТЕЛА — движение тела в поле тяготения Земли с нач. скоростью, равной нулю. П. т. происходит под действием силы тяготения, зависящей от расстояния r до центра Земли, и силы сопротивления среды (воздуха или воды), к рая зависит от скорости v движения. На… … Физическая энциклопедия
ось вращения — прямая, неподвижная относительно вращающегося вокруг неё твердого тела. Для твердого тела, имеющего неподвижную точку (например, для детского волчка), прямая, проходящая через эту точку, поворотом вокруг которой тело перемещается из данного… … Энциклопедический словарь
Падение тела — движение тела в поле тяготения Земли с начальной скоростью, равной нулю. П. т. происходит под действием силы тяготения, зависящей от расстояния r до центра Земли, и силы сопротивления среды (воздуха или воды), которая зависит от скорости… … Большая советская энциклопедия
Фигуры (тела) вращения
Наиболее распространенные фигуры (тела) вращения представлены в следующей таблице.
| Рисунок вращаемой фигуры и оси вращения | Описание вращаемой фигуры и оси вращения | Название фигуры, полученной в результате вращения | Рисунок фигуры, полученной в результате вращения |
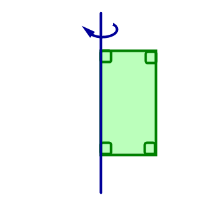 | Прямоугольник вращается вокруг прямой, проходящей через одну из его сторон | Цилиндр |  |
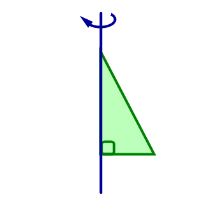 | Прямоугольный треугольник вращается вокруг прямой, проходящей через один из его катетов | Конус |  |
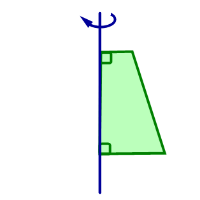 | Прямоугольная трапеция вращается вокруг прямой, проходящей через боковую сторону трапеции, перпендикулярную к ее основаниям | Усеченный конус |  |
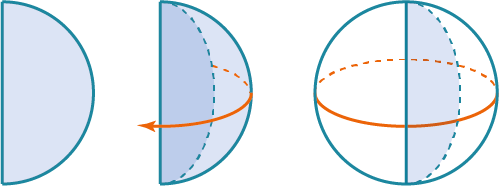
 | Полуокружность вращается вокруг прямой, проходящей через диаметр, соединяющий концы полуокружности | Сфера |  |
 | Полукруг вращается вокруг прямой, проходящий через ограничивающий полукруг диаметр | Шар |  |
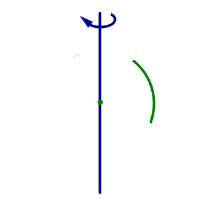 | Дуга окружности вращается вокруг прямой, проходящей через диаметр этой окружности | Сферический пояс |  |
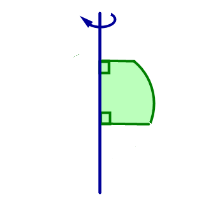 | Вращается часть полукруга, ограниченная дугой окружности, диаметром и двумя перпендикулярами, опущенными из концов дуги на диаметр. Ось вращения – прямая, проходящая через диаметр | Шаровой слой |  |
 | Круговой сектор вращается вокруг прямой, проходящей через один из радиусов, ограничивающих сектор | Шаровой сектор |  |
Вращаемая фигура и ось вращения:
Прямоугольник Прямоугольник вращается вокруг прямой, проходящей через одну из его сторон
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Прямоугольный треугольник вращается вокруг прямой, проходящей через один из его катетов
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Прямоугольная трапеция вращается вокруг прямой, проходящей через боковую сторону трапеции, перпендикулярную к ее основаниям
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Полуокружность вращается вокруг прямой, проходящей через диаметр, диаметр, соединяющий концы полуокружности
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Полукруг вращается вокруг прямой, проходящий через ограничивающий полукруг диаметр диаметр
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Дуга окружности вращается вокруг прямой, проходящей через диаметр диаметр этой окружности
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Вращается часть полукруга, ограниченная дугой окружности, диаметром и двумя перпендикулярами, опущенными из концов дуги на диаметр. Ось вращения – прямая, проходящая через диаметр диаметр
Рисунок фигуры, полученной в результате вращения:
Вращаемая фигура и ось вращения:
Круговой сектор Круговой сектор вращается вокруг прямой, проходящей через один из радиусов, радиусов, ограничивающих сектор
Рисунок фигуры, полученной в результате вращения:
Тела вращения
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости
Сегментная поверхность
Часть сферы, отделяемая от нее секущей плоскостью, называется сегментной поверхностью.
Площадь сегментной поверхности
Шаровой сегмент
Часть шара отделяемая от него секущей плоскостью, называется шаровым сегментом.
Отрезок радиуса, перпендикулярного к секущей плоскости, заключенный между этой плоскостью и сегментной поверхностью, называется высотой этой поверхности и шарового сегмента.
Площадь полной поверхности шарового сегмента
Объем шарового сегмента
Шаровой сектор
Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.
Поверхность шарового сектора складывается из кривых поверхностей шарового сегмента и конуса.
Объем шарового сектора равен объёму пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.
Шаровой слой.
Часть шара, заключенная между двумя параллельными секущими плоскостями, называется шаровым слоем.
Отрезок перпендикуляра, заключенный между параллельными секущими плоскостями, называется высотой шарового слоя и шарового пояса.
Площадь внешней поверхности шарового слоя
Площадь полной поверхности шарового слоя
Объём шарового слоя
Прямой круговой цилиндр
Цилиндр называется круговым, если его направляющая является окружностью.
Цилиндр называется прямым, если его образующая перпендикулярна основаниям.
Конус
Конус или коническая поверхность представляет собой пространственную фигуру, образованную движением прямой, проходящей через некоторую определенную точку (вершину конуса) и пересекающую заданную линию, которая называется направляющей конуса. Указанная прямая называется образующей.
Часто конусом называется пространственная фигура, ограниченная внутренней частью плоскости, пересекающей коническую поверхность, и частью конической поверхности, заключенной между вершиной и границей пересечения. Часть указанной плоскости, лежащая внутри конической поверхности, называется основанием конуса, а часть конической поверхности − боковой поверхностью.
Конус называется круговым, если в его основании лежит круг.
Конус является прямым, если его вершина проецируется в центр основания.
Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Прямой усечённый конус
Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
$P=B_1+B_2+M \Rightarrow P=r_1^2\pi+r_2^2\pi+s\pi(r_1+r_2)=\pi(r_1^2+r_2^2+s(r_1+r_2))$
$V=\frac
Осни пресек зарубљене купе:
Шар и многогранники
Призма вписанная в шар
Призма вписана в шар, если все ее вершины лежат на поверхности шара (на сфере). В этом случае также говорят, что шар описан около призмы (или сфера описана около призмы).
Призма может быть вписана в шар тогда и только тогда, когда
2) около ее основания можно описать окружность.
-Правильная треугольная призма вписана в шар:
—Правильная четырёхугольная призма вписана в шар:
—Правильная шестиугольная призма вписана в шар
—Треугольная призма, у которой в основании произвольный треугольник вписана в шар:
Пирамида вписана в шар
Если пирамида вписана в шар, то все ее вершины лежат на поверхности этого шара (на сфере), соответственно, расстояния от центра шара до вершин равны радиусу шара.
Каждая грань вписанной в шар пирамиды является вписанным в некоторую окружность многоугольником. Основания перпендикуляров, опущенных из центра шара на плоскости граней, являются центрами этих описанных окружностей. Таким образом, центр описанного около пирамиды шара — точка пересечения перпендикуляров к граням пирамиды, проведенных через центры описанных около граней окружностей.
Чаще центр описанного около пирамиды шара рассматривают как точку пересечения перпендикуляра, проведенного к основанию через центр описанной около основания окружности, и серединного перпендикуляра к боковому ребру (серединный перпендикуляр лежит в плоскости, проходящей через это боковое ребро и первый перпендикуляр (проведенный к основанию). Если около основания пирамиды нельзя описать окружность, то эта пирамида не может быть вписана в шар. Отсюда следует, что около треугольной пирамиды всегда можно описать шар, а вписанная в шар четырехугольная пирамида в основании имеет прямоугольник или квадрат.
Центр описанного около пирамиды шара может лежать внутри пирамиды, на поверхности пирамиды (на боковой грани, на основании), и вне пирамиды. Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
Около любой правильной пирамиды можно описать шар. Его центр — точка пересечения прямой, содержащей высоту пирамиды, и серединного перпендикуляра к боковому ребру.
-Правильная четырёхугольная пирамида вписанная в шар:
$r_o$- радиус окружности, описанной около основанияполупречник кружнице описане око основе
Шар, вписанный в призму
Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.
-Шар, вписан в призму, в основании которой произвольный треугольник
—Шар, вписан в призму, в основании которой квадрат
—Шар, вписан в призму, в основании которой правильный шестиугольник
Шар, вписанный в пирамиду
Шар вписан в пирамиду — значит, шар касается каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
-Шар, вписанный в правильную четырёхугольную пирамиду:
Правильный многогранник
Многогранник называется правильным, если его грани одинаковые правильные многоугольники.
Существует пять различных многогранников.
Обозначения
Тела вращения и их сечения
Телом вращения называется тело, образованное в результате вращения какой-либо линии вокруг прямой.
Примеры тел вращения.
Шар − образован полукругом, вращающимся вокруг диаметра разреза.
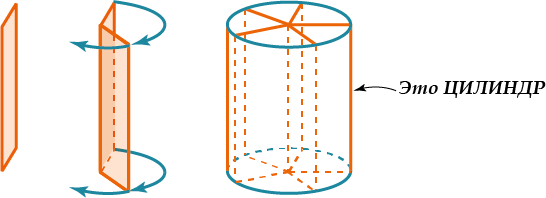
Цилиндр − образован прямоугольником, вращающимся вокруг одной из сторон.
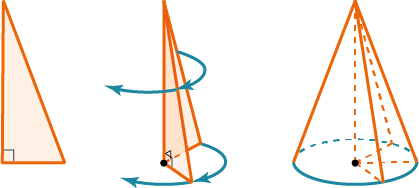
Конус − образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
При пересечении тела вращения плоскостью получается плоская фигура, ограниченная в большинстве случаев кривой линией. В частных случаях фигурой сечения может быть прямоугольник (для цилиндра) и треугольник (для конуса).
Осевым сечением цилиндра называется сечение плоскостью, проходящей через ось цилиндра. Осевое сечение цилиндра – прямоугольник, две стороны которого – образующие цилиндра, а две другие стороны – диаметры оснований цилиндра.
Секущая плоскость, перпендикулярная оси цилиндра, пересекает его по кругу.
Если плоскость проходит через высоту конуса FO, то сечение конуса этой плоскостью называют осевым и оно представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса, а боковыми сторонами – образующие конуса.
Сечение поверхности цилиндра
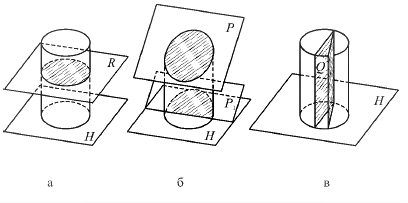
Бывают следующие случаи сечения поверхности прямого кругового цилиндра плоскостью:
1) окружность, если секущая плоскость Р перпендикулярна оси цилиндра, причем она параллельна основанию цилиндра;
2) эллипс, если секущая плоскость Р не перпендикулярна и не параллельна оси цилиндра;
3) пара прямых, если секущая плоскость Q содержит ось цилиндра или параллельна ей.
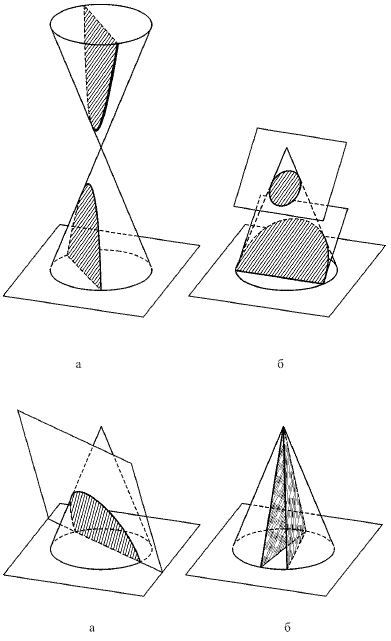
Рис. 104. Возможные случаи сечения поверхности цилиндра плоскостью: а – окружность; б – эллипс; в – пара прямых
Сечение поверхности конуса
В общем случае круговая коническая поверхность включает в себя две совершенно одинаковые полости, которые имеют общую вершину. Образующие одной полости представляют собой продолжение образующих другой полости.
Бывают различные случаи сечения поверхности кругового конуса плоскостью.
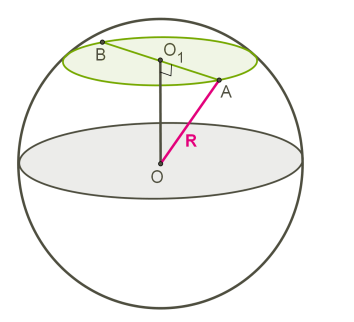
1. Эллипс, если секущая плоскость не параллельна ни одной образующей (рис. 107 б). Здесь секущая плоскость пересекает поверхность только одной полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса меньше угла, который образующая конуса составляет с основанием конуса. Здесь угол является углом, который образующая составляет с основанием.
Рис. 107. Различные случаи сечения поверхности кругового конуса плоскостью: а – гипербола; б – эллипс; в – парабола; г – пара прямых
2. Парабола, если секущая плоскость параллельна только одной образующей (рис. 107 в).
3. Гипербола, если секущая плоскость параллельна двум образующим (рис. 107 а). При этом секущая плоскость пересекает обе полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса больше угла.
4. Пара прямых, если секущая плоскость проходит через вершину конуса и угол ее наклона к основанию конуса больше угла. Этот случай иногда рассматривают как частный случай гиперболы.
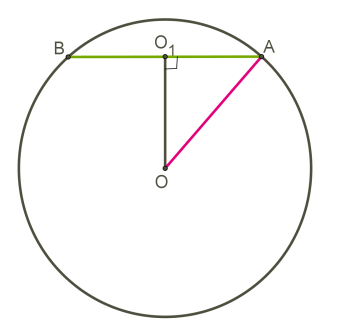
Сечение шара
Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара). Основание перпендикуляра, проведенного из центра шара к пересекаемой плоскости, есть центр круга, полученного в сечении.
При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).