тело лежит на наклонной плоскости составляющей с горизонтом угол 30 при каком
Тело лежит на наклонной плоскости составляющей с горизонтом угол 30 при каком
наклонная плоскость составляет горизонтом угол
Через блок, укрепленный на вершине двух наклонных плоскостей, составляющих с горизонтом углы α = 28° и β = 40°, перекинута нить, к которой прикреплены грузы с одинаковыми массами. Считая нить и блок невесомыми и пренебрегая трением, определите ускорение a грузов.
Тело лежит на наклонной плоскости, составляющей с горизонтом угол α = 4°. Ускорение, с которым скользит тело, а. Коэффициент трения равен k = 0,03. За время t тело проходит 100 м пути. Найти время t, скорость v, ускорение a.
Тело лежит на наклонной плоскости, составляющей с горизонтом угол α. Ускорение, с которым скользит тело, а. Коэффициент трения равен k. За время t тело проходит 100 м пути. Найти угол α, скорость v, ускорение a.
На вершине наклонной плоскости, составляющей с горизонтом угол 19 град., укреплен невесомый блок. Две гири равной массы 5 кг соединены нитью, перекинутой через блок. При этом одна из гирь лежит на наклонной плоскости, а другая висит на нити вертикально, не касаясь плоскости. Найти натяжение нити. Трением в блоке и трением о плоскость пренебречь.
Тело лежит на наклонной плоскости, составляющей с горизонтом угол α = 4°. При каком предельном коэффициенте трения к тело начнет скользить по наклонной плоскости? С каким ускорением а будет скользить тело по плоскости, если коэффициент трения k = 0,03? Какое время t потребуется для прохождения при этих условиях пути s = 100 м? Какую скорость v будет иметь тело в конце пути?
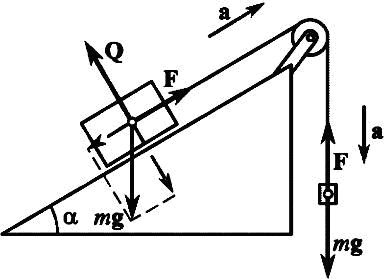
Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α = 30°. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити T. Трением гири о наклонную плоскость и трением в блоке пренебречь.
Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α = 30°. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити T. Коэффициент трения гири 2 о наклонную плоскость k = 0,1.
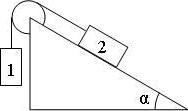
Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы α = 30° и β = 45°. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити T. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы α = 30° и β = 45°. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити T. Коэффициенты трения гирь 1 и 2 о наклонные плоскости k1 = k2 = 0,1.
Определить работу силы трения при спуске тела массой 5 кг по наклонной плоскости, составляющей с горизонтом угол 60°. Длина наклонной плоскости 1 м. Коэффициент трения равен 0,2.
Тело лежит на наклонной плоскости, составляющей с горизонтом угол α = 4°. Ускорение, с которым скользит тело, а. Коэффициент трения равен k = 0,3. За время t тело проходит 100 м пути. Найти время t, скорость v, ускорение a.
Тело лежит на наклонной плоскости, составляющей с горизонтом угол α. Ускорение, с которым скользит тело, а. Коэффициент трения равен k. За время t тело проходит 100 м пути. Найти угол α, скорость v, ускорение a.
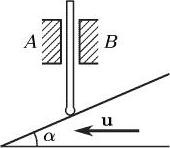
На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству АВ. С какой скоростью v поднимается стержень, если наклонная плоскость движется влево со скоростью u?
Шарик скатывается с высоты 16 см по наклонной плоскости, составляющей угол 48 градусов с горизонтом. Скатившись, он тут же поднимается по другой наклонной плоскости, наклоненной под тем же углом к горизонту. Найти частоту колебаний шарика. Трение не учитывать.
Брусок скатывается ускоренно с наклонной плоскости, составляющей с горизонтом угол α = 30°. Определить скорость v бруска у основания наклонной плоскости, если коэффициент трения μ = 0,1, а высота, наклонной плоскости Н = 2 м.
С наклонной плоскости, составляющей с горизонтом угол 45° скатывается диск. Длина плоскости 3 м. Пренебрегая трением, вычислите линейное ускорение центра массы диска, время скатывания и скорость в конце наклонной плоскости.
С наклонной плоскости, составляющей с горизонтом угол 60°, скатывается обруч. Длина плоскости 6 м. Пренебрегая трением, вычислите линейное ускорение центра масс обруча, время скатывания и скорость в конце наклонной плоскости.
По наклонной плоскости, составляющей с горизонтом угол 30°, спускается без начальной скорости тело. Коэффициент трения f = 1/(2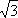
Тело лежит на наклонной плоскости составляющей с горизонтом угол 30 при каком
Тело массой покоится на наклонной плоскости, составляющей с горизонтом угол
Коэффициент трения равен
Чему равна сила трения, действующая на тело?
1)
2)
4)
Тело покоится, следовательно, его ускорение равно нулю. На него действует три силы: сила тяжести, направленная вниз, сила реакции опоры, направленная перпендикулярно плоскости, и сила трения покоя, мешающая телу скатиться и направленная вверх вдоль плоскости. Рассмотрим второй закон Ньютона в проекции на ось, параллельную плоскости: Таким образом, сила трения равна
Нет, так нельзя. То, что Вы пишете — это сила трения скольжения, такую формулу можно использовать только тогда, когда тело движется. А у нас тело покоится, значит, возникает сила трения покоя, которая попросту уравновешивает внешнее воздействие.
Вот смотрите, рассмотрим книгу, лежащую на горизонтальной поверхности. Величина в этом случае, естественно, отлична от нуля. А вот сила трения равна нулю. Действительно, на книгу не действует никаких внешних сил в горизонтальном направлении, если бы на нее начала действовать сила трения, то, по второму закону Ньютона, книга начала бы сама по себе двигаться по столу 🙂 Да и вообще, в этом примере даже непонятно, куда направить эту силу, ведь все направления тут эквивалентны.
Посмотрите в связи с этим еще задачу 3512.
то есть при силе трения покоя коэффициент трения не учитывается не пойму
Коэффициент трения и сила реакции определят максимальную силу трения покоя. Формула работает только для силы трения скольжения. Представьте себе книгу на горизонтальном шероховатом столе. Вы ведь согласитесь с тем, что коэффициент трения есть, сила реакции опоры есть, а силы трения нет?
ведь если не учитывать коэффицент трения то на наклонной плоскости тело в любом случае будет скатываться вниз под действием силы тяжести
Коэффициент трения как раз отличен от нуля, более того, он достаточен для того, чтобы удерживать тело на наклонной плоскости. То есть косвенным образом ответ зависит от
В задаче 3556 на самом деле два правильных ответа: 2 и 4.
Номер 4 соответствует приведенному на сайте решению, а номер 2 соответствует, если решать задачу через формулу Fтр=ϻN и выражать N через проекцию второго закона Ньютона на ось Y. А N в этом случае будет как раз равна mgcosα. Правильность решения подтверждается еще и тем, что коэффициент трения по наклонной плоскости определяется еще и как тангенс угла наклона. Если мы приравняем оба выражения для Fтр и выразим ϻ, то как раз и получим тангенс угла наклона.
Тело лежит на наклонной плоскости составляющей с горизонтом угол 30 при каком
Тело массой покоится на наклонной плоскости, составляющей с горизонтом угол
Коэффициент трения равен
Чему равна сила трения, действующая на тело?
1)
2)
4)
Тело покоится, следовательно, его ускорение равно нулю. На него действует три силы: сила тяжести, направленная вниз, сила реакции опоры, направленная перпендикулярно плоскости, и сила трения покоя, мешающая телу скатиться и направленная вверх вдоль плоскости. Рассмотрим второй закон Ньютона в проекции на ось, параллельную плоскости: Таким образом, сила трения равна
Нет, так нельзя. То, что Вы пишете — это сила трения скольжения, такую формулу можно использовать только тогда, когда тело движется. А у нас тело покоится, значит, возникает сила трения покоя, которая попросту уравновешивает внешнее воздействие.
Вот смотрите, рассмотрим книгу, лежащую на горизонтальной поверхности. Величина в этом случае, естественно, отлична от нуля. А вот сила трения равна нулю. Действительно, на книгу не действует никаких внешних сил в горизонтальном направлении, если бы на нее начала действовать сила трения, то, по второму закону Ньютона, книга начала бы сама по себе двигаться по столу 🙂 Да и вообще, в этом примере даже непонятно, куда направить эту силу, ведь все направления тут эквивалентны.
Посмотрите в связи с этим еще задачу 3512.
то есть при силе трения покоя коэффициент трения не учитывается не пойму
Коэффициент трения и сила реакции определят максимальную силу трения покоя. Формула работает только для силы трения скольжения. Представьте себе книгу на горизонтальном шероховатом столе. Вы ведь согласитесь с тем, что коэффициент трения есть, сила реакции опоры есть, а силы трения нет?
ведь если не учитывать коэффицент трения то на наклонной плоскости тело в любом случае будет скатываться вниз под действием силы тяжести
Коэффициент трения как раз отличен от нуля, более того, он достаточен для того, чтобы удерживать тело на наклонной плоскости. То есть косвенным образом ответ зависит от
В задаче 3556 на самом деле два правильных ответа: 2 и 4.
Номер 4 соответствует приведенному на сайте решению, а номер 2 соответствует, если решать задачу через формулу Fтр=ϻN и выражать N через проекцию второго закона Ньютона на ось Y. А N в этом случае будет как раз равна mgcosα. Правильность решения подтверждается еще и тем, что коэффициент трения по наклонной плоскости определяется еще и как тангенс угла наклона. Если мы приравняем оба выражения для Fтр и выразим ϻ, то как раз и получим тангенс угла наклона.
Тело лежит на наклонной плоскости составляющей с горизонтом угол 30 при каком
Небольшое тело кладут на наклонную плоскость, угол при основании которой можно изменять. Если угол при основании наклонной плоскости равен 30°, то тело покоится и на него действует такая же по модулю сила трения, как и в случае, когда угол при основании наклонной плоскости равен 45°. Чему равен коэффициент трения между наклонной плоскостью и телом? Ответ округлите до десятых долей.
Запишем второй закон Ньютона в первом случае, когда тело покоится
В проекции на ось, параллельную наклонной плоскости
Если бы во втором случае тело тоже покоилось, то сила трения была бы и не могла бы равняться
Значит, при угле 45° тело скользит. Запишем второй закон Ньютона во втором случае в проекции на ось, перпендикулярную плоскости
Сила трения скольжения равна
Приравнивая силы, получаем
Выразим отсюда коэффициент трения между наклонной плоскостью и телом
Некоторые читатели могут задаться вопросом, почему не выразить силу трения в первом случае как Дело в том, что сила трения равна
только в том случае, когда тело движется, в этом случае сила трения равна силе трения скольжения. В первом же случае тело покоится и сила трения равна не силе трения скольжения, а силе трения покоя:
Тело лежит на наклонной плоскости, составляющей с горизонтом угол. При каком предельном значении коэффициента
Часть текста скрыта. После покупки Вы получаете полную версию
Тело лежит на наклонной плоскости, составляющей с горизонтом угол.…
Тело лежит на наклонной плоскости, составляющей с горизонтом угол. При каком предельном значении коэффициента трения тело начнет скользить по наклонной плоскости? С каким ускорением будет двигаться оно по плоскости, если коэффициент трения равен 0,03? Сколько времени потребуется для прохождения при этих условиях 100 м пути?
Сила, скатывающая тело с поверхности
Соскальзывание возможно до тех пор, пока сила трения меньше или равна скатывающей силе
По второму закону Ньютона ускорение соскальзывающего тела
Так как движение равноускоренное, считая начальную скорость тела равной нулю, зависимость пройденного пути имеет вид:
По закону сохранения энергии
Определить частоту гармонических колебаний диска радиусом 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
Период колебаний физического маятника
Сколько атомов содержится в 1 г ртути? Считая атомы шариками, соприкасающимися друг с другом, найдите их диаметр. Значение плотности ртути возьмите из справочных таблиц.
Количество вещества, соответствующее данной массе
Плотность ртути. так как N молекул имеют массу m
Баллон объемом 0,02 м3, содержащий воздух под давлением. Па, соединяют с пустым баллоном объемом 0,04 м3. Найти, какое давление установится в сосудах. Молярная масса воздуха равна.
Когда заполнен один баллон, уравнение состояния газа имеет вид
Так как масса и температура газа остаются неизменными
Определить молярные теплоемкости газа, если его удельные теплоемкости.
Молярные теплоемкости по определению
Они связаны с удельными соотношениями
Решив полученную систему относительно. (количество степеней свободы молекулы газа) и М (молярная масса газа), найдем
В цикле Карно газ получил от нагревателя при температуре 400К количество тепла, равное 500 Дж, и совершил работу 100 Дж. Определить: 1) термический КПД цикла; 2) температуру холодильника; 3) переданное холодильнику количество тепла.
По определению КПД тепловой машины
КПД тепловой машины, работающей по циклу Карно, можно определить по формуле