Tgx 3 чему равен
tg x = 3 решение
Доброй ночи!У меня снова возникли проблемы с решением тригонометрических уравнений, и я до сих пор не могу понять, как и в какой последовательностью что-то надо делать. Надеюсь Вы мне поможете решить вот такое уравнение: tg x = 3. Надеюсь, хоть Вы сможете мне это объяснить
Доброй Вам ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение. Но это, на самом деле, не так страшно и не так сложно. Прежде, чем разобраться с Вашей уравнением tg x = 3, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло. Но для решения этого уравнения есть определённое правило решения подобных уравнений, которое примет такой общий вид:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
если бы у нас было классическое число из таблицы, которое нужно было бы найти, то мы бы с Вами воспользовались уже известной Вам таблицей. И уже исходя из этого получили бы какое-то значение, которое могли бы с Вами использовать.
И мы бы С вами продолжали решать наше уравнение. Но так как с этим не сложилось, то мы с Вами просто напросто ничего не меняем и записываем ответ в таком виде: :
Ответ: 
Надеюсь, Вы поняли почему, зачем и как мы с Вами делали. Удачи Вам в решении подобных заданий. Удачи Вам!
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a
Уравнение sin(х) = а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Уравнение вида a sin(x) + b cos(x) = c
Используя формулы \( \sin(x) = 2\sin\frac
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, \( \sqrt
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Объяснение и обоснование
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2

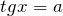
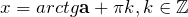






.png)