треугольники с какими сторонами будут прямоугольными

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Источник

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

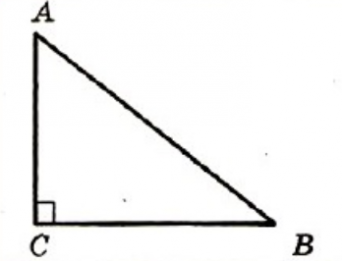
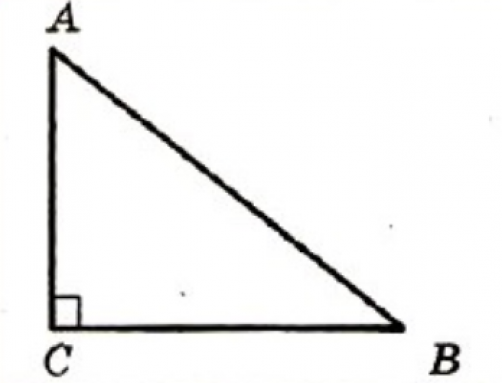
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

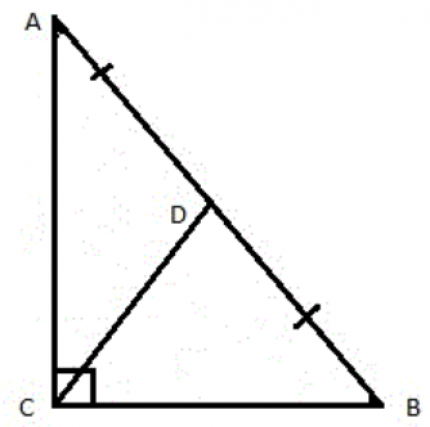
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Источник

Прямоугольный треугольник, свойства, признаки и формулы

Прямоугольный треугольник, свойства, признаки и формулы.

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Прямоугольный треугольник (понятие, определение):

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Сторона, противоположная прямому углу, называется гипотенузой. Гипотенуза (с греч. ὑποτείνουσα – «натянутая») – это самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

Рис. 1. Прямоугольный треугольник

АВ, АС – катеты прямоугольного треугольника, ВС – гипотенуза прямоугольного треугольника, ∠ ВАС = 90°

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый острый угол равен 45°.

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.

1. Равенство по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Рис. 2. Равенство прямоугольных треугольников по двум катетам

2. Равенство по катету и прилежащему острому углу.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу

3. Равенство по гипотенузе и острому углу.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу

4. Равенство по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету

5. Равенство по катету и противолежащему острому углу.

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу

Свойства прямоугольного треугольника:

1. В прямоугольном треугольнике сумма двух острых углов равна 90°.

И наоборот, если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

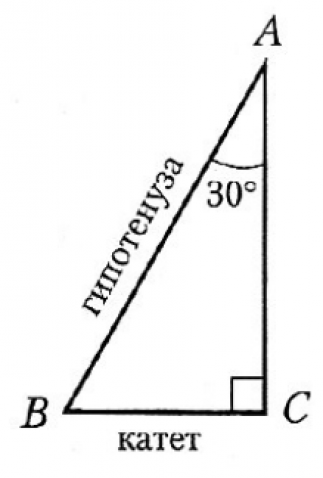
Рис. 7. Прямоугольный треугольник с острым углом 30˚

3. Теорема Пифагора:

Сумма квадратов катетов равна квадрату гипотенузы.

где a, b – катеты, c – гипотенуза.

4. В прямоугольном треугольнике центр описанной окружности – есть середина гипотенузы.

И соответственно радиус описанной окружности (R) равен половине гипотенузы.

,

Рис. 9. Прямоугольный треугольник и описанная окружность

5. В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы.

Рис. 10. Прямоугольный треугольник и медиана, падающая на гипотенузу

АМ – медиана прямоугольного треугольника, падающая на гипотенузу, АМ = ВМ = МС, АМ = ВС/2

6. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника подобные исходному.

Рис. 11. Прямоугольный треугольник и высота, проведенная из вершины прямого угла

Формулы прямоугольного треугольника:

Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).

Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:

a​ 2 ​​ = c​ 2 ​​ – b​ 2 ​​ ,

b​ 2 ​​ = c​ 2 – a​ 2 ​​.

Формула радиуса вписанной окружности (r):

.

Рис. 12. Прямоугольный треугольник и вписанная окружность

Формула радиуса описанной окружности (R):

.

Формулы площади (S) прямоугольного треугольника:

.

Формулы высоты (h)прямоугольного треугольника:

.

Источник

Прямоугольные треугольники

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

Площадь прямоугольного треугольника равна половине произведения его катетов

Подставим найденное значение в формулу косинуса

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Источник

Треугольники общего вида

Треугольники общего вида.

Основные свойства треугольников:

Свойства медиан:

1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.

2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.

3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.

Свойства высот:

1. Три высоты (или их продолжения) пересекаются в одной точке.

2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.

3. Высоты треугольника обратно пропорциональны его сторонам:

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.

2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)

4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

Значения тригонометрических функций некоторых углов:

Тригонометрические тождества:

1. Основное тригонометрическое тождество:

2. Связь между тангенсом и косинусом одного и того же угла:

3. Связь между котангенсом и синусом одного и того же угла:

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Признаки подобия треугольников:

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Источник