у каких фигур все стороны равны

Какие фигуры, у которых все стороны равны?

Какие фигуры, у которых все стороны равны?

Это любые правильные многоугольники

Какую фигуру можно построить последовательно соединяя середины сторон параллелограмма?

Какую фигуру можно построить последовательно соединяя середины сторон параллелограмма.

Чему равно соотношение площадей подобных фигур, если отношение их сторон равно 2 / 3 (дробь)?

Чему равно соотношение площадей подобных фигур, если отношение их сторон равно 2 / 3 (дробь).

Может ли быть, что у четырёхугольника две противоположные стороны равны а две другие нет и как называется эта фигура?

Может ли быть, что у четырёхугольника две противоположные стороны равны а две другие нет и как называется эта фигура?

Какие фигуры называются равными?

Какие фигуры называются равными.

В прямоугольнике одна из его сторон равна 5?

В прямоугольнике одна из его сторон равна 5.

Найдите другую сторону, если площадь данной фигуры равна 30.

Какие фигуры называются равными?

Какие фигуры называются равными?

Какие фигуры являются равными?

Какие фигуры являются равными.

Какие фигуры называются равными?

Какие фигуры называются равными?

СРОЧНО?

Сторона квадрата равна 12см.

Каждая из сторон квадрата разделена на три равные части.

Найдите площадь закрашенной фигуры.

Какие фигуры называются равными?

Какие фигуры называются равными?

Билет 2 1)диагонали параллелограмма точкой пересечения делятся попалам 2)любая диагональ параллелограмма делит его на два равных треугольника 3)сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон 4)площа..

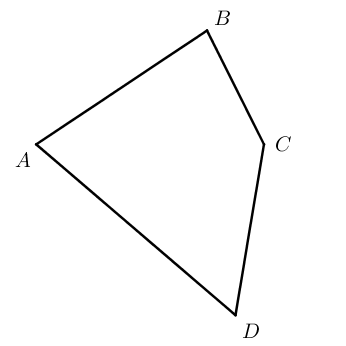
По первой картинке : 1) и 3), второе неверно, т. К. против меньшего угла лежит меньшая сторона. По второй картинке : 3), возможно 1)но это не точно, так что говори 3).

Источник

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
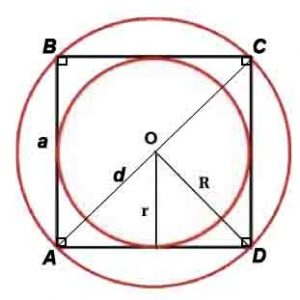
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
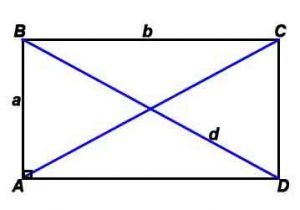
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
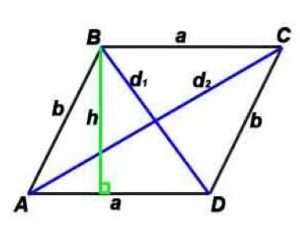
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

Свойства:

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

Свойства:

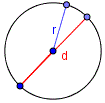
Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
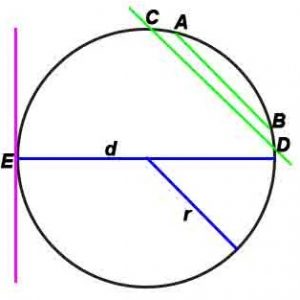
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Геометрия. Урок 4. Четырехугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

Площадь параллелограмма можно найти по трём формулам.

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

Площадь ромба можно найти по трём формулам.

Как произведение стороны ромба на высоту ромба.

Как квадрат стороны ромба на синус угла между двумя сторонами.

Как полупроизведение диагоналей ромба.

Прямоугольник

Свойства прямоугольника:

Площадь прямоугольника можно найти по двум формулам:

Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

Площадь квадрата можно вычислить по двум формулам:

Как квадрат стороны.

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Свойства трапеции:

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Источник