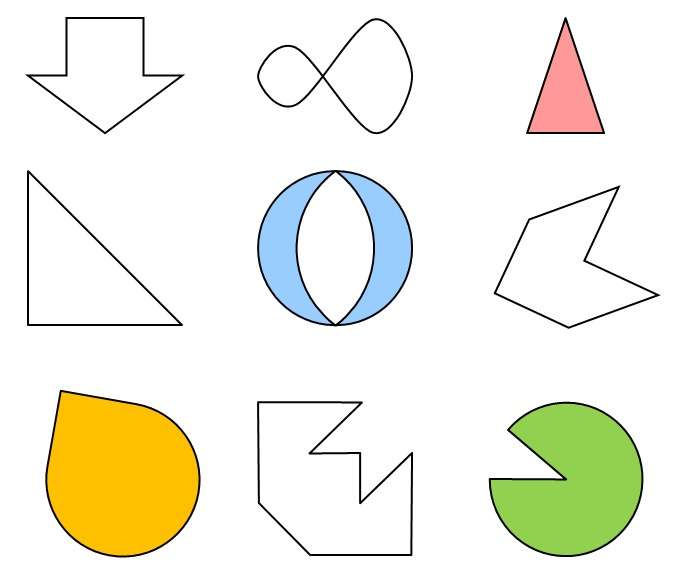
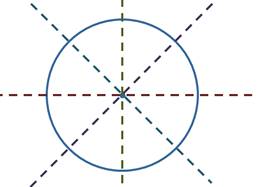
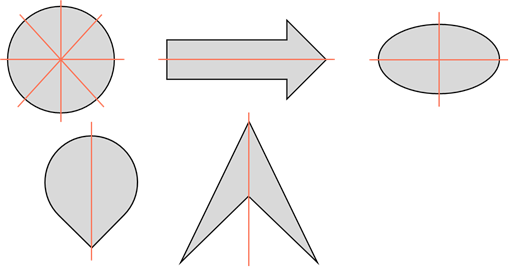
у какой фигуры четыре оси симметрии

Симметрия

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

Вывод

Источник

Осевая и центральная симметрии

Урок 8. Геометрия 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Осевая и центральная симметрии»

Наверняка, каждый из вас не раз слышал слово «симметричный». К чему же это интересное слово можно отнести?

Возьмем, к примеру, листок какого-нибудь растения. Если сложить его пополам, то можно заметить, что каждая из получившихся частей (левая и правая) окажутся одинаковыми, т.е. симметричными.

Аналогично можно поступить и с некоторыми цветами.

В животном мире также можно заметить такую особенность. Вот, например, посмотрим на бабочку. Ее крылья симметричны относительно тельца.

А если посмотреть на здания, которые нас окружают? То снова заметим симметричные части. То же самое вы можете обнаружить в искусстве, да и просто в быту.

Теперь поговорим о том, что же в математике понимают под словом «симметричный», или «симметрия».

В переводе с греческого слово «симметрия» означает соразмерность, то есть схожесть, одинаковость. Это свойство геометрических объектов сохранять расположение элементов фигуры относительно оси или центра симметрии в неизменном состоянии при некоторых преобразованиях.

На этом уроке мы поговорим об осевой симметрии (симметрии относительно прямой) и о центральной симметрии (симметрии относительно точки).

Начнём с осевой симметрии.

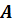
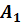
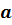
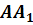
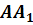
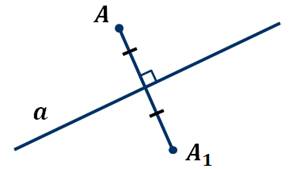
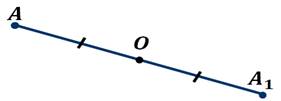
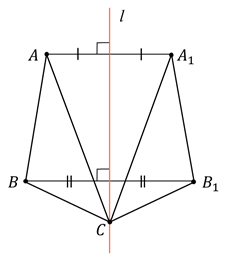
Точки и называются симметричными относительно прямой , если эта прямая проходит через середину отрезка и перпендикулярна отрезку .

Давайте найдём точку симметричную данной относительно прямой.

Возьмём прямую а и точку А. Проведём через точку А прямую АО, перпендикулярную прямой а. Затем отложим на прямой АО отрезок ОА₁, равный отрезку АО.

Таким образом, получили точку А₁ симметричную точке А относительно прямой а.

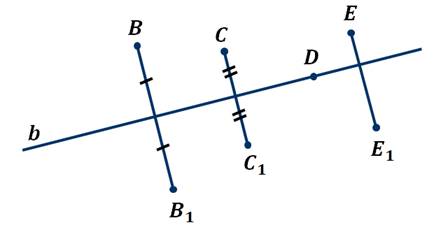
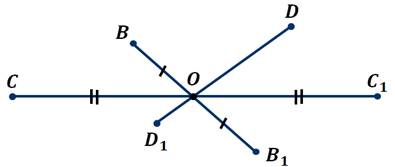
На следующем рисунке точки B и B₁ симметричны относительно прямой b, точки C и C₁ также симметричны относительно прямой b, а вот точка D симметрична самой себе относительно прямой b. Точки Е и E₁ не симметричны относительно прямой b, так как прямая b проходит не через середину отрезка EE₁.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.

Прямую а называют осью симметрии фигуры.

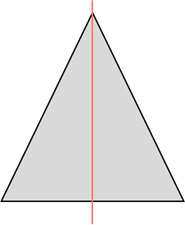
Осевой симметрией обладает равнобедренный треугольник.

Он имеет одну ось симметрии, на которой расположена биссектриса, проведённая из вершины к основанию. То есть, если мы перегнём равнобедренный треугольник по оси симметрии, то каждая точка одной половины будет иметь симметричную ей точку на второй половине.

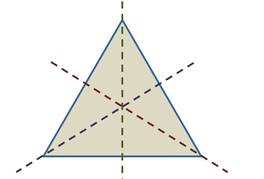
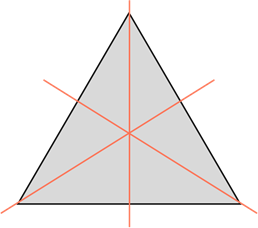
Равносторонний треугольник также обладает осевой симметрией и имеет три оси симметрии, на которых расположены биссектрисы углов треугольника.

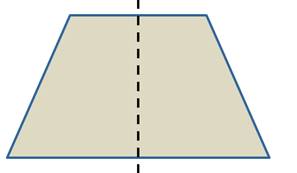
Равнобедренная трапеция имеет ось симметрии, на которой лежит прямая проходящая через середины её оснований.

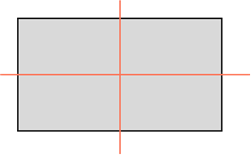
Прямоугольник имеет две оси симметрии, которые проходят через середины его противолежащих сторон.

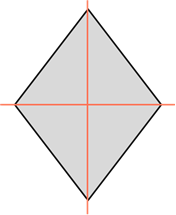
Ромб также имеет две оси симметрии, на которых расположены его диагонали…

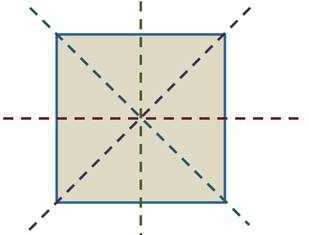
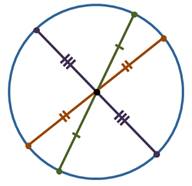
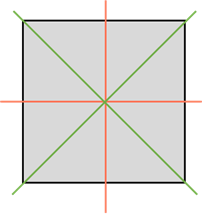
Квадрат имеет четыре оси симметрии, так как одновременно является и прямоугольником и ромбом.

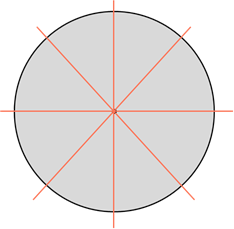
А вот у окружности каждая прямая, проходящая через её центр, является осью симметрии. Так как таких прямых можно провести бесконечно много, то и осей симметрии у окружности бесконечно много.

Но есть и фигуры, у которых нет ни одной оси симметрии. Примерами таких фигур являются разносторонний треугольник. Или параллелограмм, который не является прямоугольником или ромбом.

Теперь поговорим о центральной симметрии, то есть симметрии относительно точки.

Точки А и A₁ называются симметричными относительно точки О, если точка О – середина отрезка АА₁.

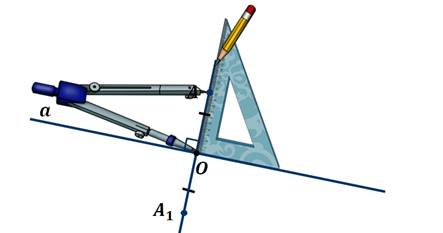
Давайте найдём точку симметричную данной относительно точки О.

Возьмём произвольные точки А и О. И проведём через них прямую АО. Затем на этой прямой отложим отрезок ОА₁ равный отрезку АО.

Таким образом, мы получили точку А₁ симметричную точке А относительно точки О.

Посмотрите на следующий рисунок.

Здесь точка B симметрична точке B₁ относительно точки О. Точки C и C₁ также симметричны относительно точки О. Точка О симметрична сама себе. А точки D и D₁ не симметричны относительно точки О, так как отрезки DO и OD₁ не равны.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Точку О называют центром симметрии фигуры.

Центральной симметрией обладает окружность.

Её центр является центром симметрии. То есть, для любой точки окружности существует ей симметричная относительно центра.

Параллелограмм также обладает центральной симметрией. Центром его симметрии является точка пересечения диагоналей.

Раз параллелограмм обладает центральной симметрией, то известные нам прямоугольник, ромб и квадрат также обладают центральной симметрией, центром которой является точка пересечения их диагоналей.

Центральной симметрией обладает и прямая, причём любая точка прямой является центром её симметрии.

Примером фигуры, не обладающей центральной симметрией, является произвольный треугольник.

А вот, например, такие фигуры, как прямоугольник, ромб, квадрат, окружность имеют обе симметрии (осевую и центральную).

Источник

Учебник Моро 4 класс 1 часть. Страница 31

СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ

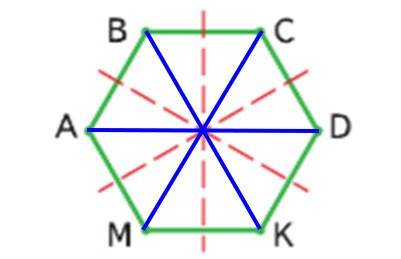
1. Задание «Проведи в шестиугольнике с равными сторонам все оси симметрии» ученик выполнил так.

Все ли оси симметрии этой фигуры он провёл? Нет, можно провести ещё три оси симметрии (синие отрезки):

Запиши названия тех отрезков, которые будут осями симметрии шестиугольника ABCDKM, и которых нет на чертеже.

2. Выбери все высказывания, верные для этого рисунка.

1) Если фигура не жёлтого цвета, то это многоугольник — неверно, так как красная фигура является кругом, а не многоугольником.

2) Если фигура синего цвета, то это четырёхугольник — неверно, так как одна из синих фигур — пятиугольник.

3) Если фигура не закрашена, то это прямоугольный треугольник — верно.

4) Если фигура зелёного цвета, то у неё 6 осей симметрии — неверно, так как у квадрата 4 оси симметрии.

Ответ: верное высказывание № 3.

Закончи высказывания, верные для данного рисунка.

3. Вычислительная машина работает так:

1) Какое число будет получаться на выходе из машины, если в неё ввели число: 2; 200; 100; 50; 300?

Ответ: 199, 19 999, 9 999, 4 999, 29 999.

2) Какое число ввели в машину, если на выходе получили число: 199; 5999; 399?

Источник

Симметрия

Урок 29. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Симметрия»

Опыты с зеркалами, которые мы проводили на прошлом занятии, позволили нам прикоснуться к удивительному миру симметрии.

В переводе с греческого слово «симметрия» означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то, что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким образом…

А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура).

Поэтому такая симметрия называется зеркальной (или осевой, если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии.

Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.

С симметрией мы постоянно встречаемся в повседневной жизни. Люди используют симметрию в орнаментах, предметах быта, технике. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придаёт гармоничность, законченность. Симметрия также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.

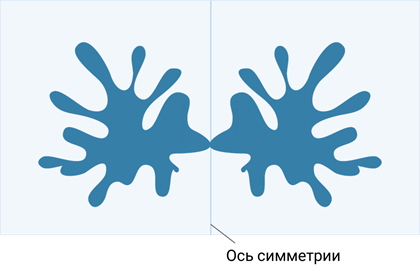
Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил. Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии кляксы.

Получается, что клякса имеет одну (вертикальную) ось симметрии.

А вот у снежинки 6 линий сгиба и все они являются осями симметрии.

У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.

Так, прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон. То есть, вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии, половинки фигуры совпадут.

Ромб также обладает двумя осями симметрии. Это прямые, которые содержат его диагонали.

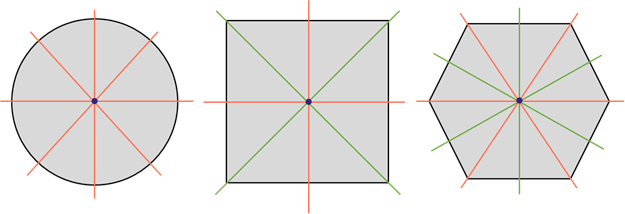
Квадрат имеет четыре оси симметрии. Две проходят через середины его противоположных сторон. И ещё две – это прямые, которые содержат его диагонали.

Круг. Его осью симметрии является любая прямая, которая проходит через его центр, то есть содержит диаметр круга. А значит, круг имеет бесконечно много осей симметрии

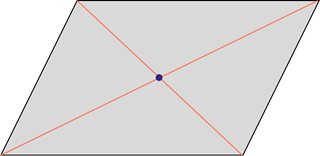
Теперь посмотрите на следующую фигуру. Это произвольный параллелограмм. У него нет ни одной оси симметрии.

У произвольного треугольника тоже нет осей симметрии.

У равнобедренного треугольника есть одна ось симметрии.

У равностороннего (то есть у правильного) треугольника – три оси симметрии.

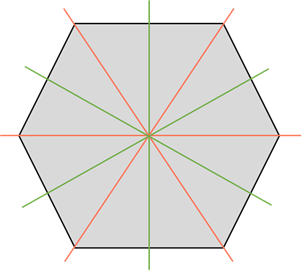
Теперь посмотрите на шестиугольник. У него три оси симметрии, которые проходят через противоположные вершины, и ещё три оси, которые проходят через середины противоположных сторон. То есть всего шесть осей симметрии.

Таким образом, мы можем сказать, что круг – «самая симметричная» фигура из рассмотренных, так как он имеет бесконечно много осей симметрии.

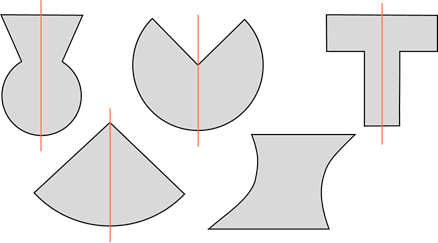
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из них лишняя.

Итак, первая фигура напоминает замочную скважину. Она имеет одну ось симметрии.

Вторая фигура тоже имеет одну ось симметрии.

У третьей фигуры (в виде буквы Т) одна ось симметрии.

У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси симметрии. И поэтому она лишняя.

Теперь давайте посмотрим на следующие пять фигур. Что у них общего?

Первая фигура – круг. Выше мы выяснили, что у круга бесконечно много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая фигура имеет хотя бы одну ось симметрии.

На предыдущем занятии мы с вами проводили опыт с двумя плоскими зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали симметричные фигуры.

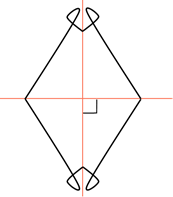
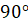
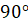
Давайте изобразим в виде прямых два зеркала под углом друг к другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно, что угол ними равен .

Посмотрите на рассмотренные выше фигуры, которые имеют две оси симметрии. Угол между осями равен .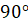

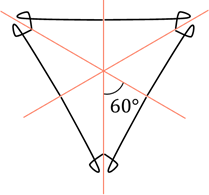
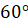
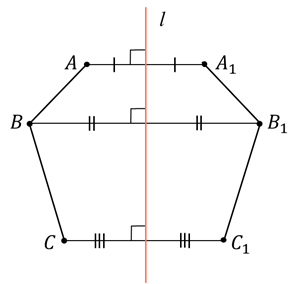
Если, например, мы поставим зеркала под углом друг к другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси симметрии.

Давайте научимся точно строить отражение фигуры в зеркале. Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную 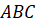и построим её отражение в зеркале.

Итак, из вершин , и опускаем перпендикуляры на прямую l. Затем продолжаем их «за зеркало» на такое же расстояние (равное длине соответствующего отрезка). Получаем точки , и . Соединяем эти точки. Ломаная является отражение ломаной .

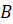
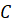
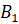
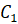
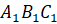
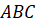
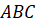
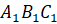
Можно сказать, что ломаная симметрична ломаной относительно прямой l.

Построим с вами треугольник, симметричный треугольнику 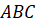относительно прямой l.

Из вершин и опустим перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние (равное длине соответствующего отрезка). Получим точки и .

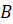
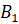
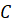
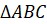
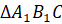
При этом точка осталась на месте. Она лежит на оси симметрии. Она симметрична сама себе. и симметричны относительно прямой l.

А сейчас посмотрите на рисунок.

Давайте выясним, симметрична ли точка точке относительно прямой l. Для этого мы соединим точки и . Затем с помощью угольника проверим, перпендикулярна ли прямая l отрезку . Перпендикулярна.

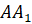
Потом с помощью линейки проверим, делит ли прямая l отрезок и пополам. Делит.

Значит, точки и симметричны относительно прямой l.

Кроме симметрии относительно прямой существует ещё симметрия относительно точки, так называемая центральная симметрия. Она характеризуется наличием центра симметрии – точки О, которая обладает определённым свойством. Можно сказать, что точка О является центром симметрии, если при повороте вокруг точки О на 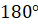фигура переходит сама в себя.

Понятие центральной симметрии распространяется и на трёхмерное пространство.

Проверить, является ли фигура центрально-симметричной или нет, можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем, проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру на 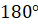вокруг иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.

Сейчас посмотрите на плоские фигуры, которые имеют и центр симметрии, и оси симметрии.

Это круг. Выше мы сказали, что он имеет бесконечно много осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии круга является его центр.

Квадрат имеет четыре оси симметрии. Центром симметрии квадрата является точка пересечения его диагоналей.

У шестиугольника шесть осей симметрии. Центром его симметрии является точка пересечения его диагоналей.

Выше мы сказали, что произвольный параллелограмм не имеет ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его диагоналей.

А вот, например, равнобедренный треугольник имеет ось симметрии, но не имеет центра симметрии. То же самое можно сказать и про пятиугольник, у которого есть оси симметрии, но центра симметрии нет.

Источник