у какой фигуры шесть сторон

Столбы базальтов от извержения старого вулкана. Снежинка. Пчелиные ульи. Кораллы, кристаллы и множество других структур, как биологических, так и небиологических, имеют форму шестиугольника. Почему природа, которая часто кажется такой беспорядочной и неправильной, предпочитает именно эту форму? Оказывается, все дело в геометрии и физике.

Соты строятся из пчелиного воска, вырабатываемого рабочими пчелами. Они вырабатывают воск из специальных желез в своем теле, которые затем смешивают с небольшим количеством меда и пыльцы, которую они разжевывают, чтобы получить пчелиный воск. Соты будут служить сосудами для хранения меда, а также камерами для выращивания молодых пчел.

Все это хорошо и замечательно, но почему шестиугольники?

Вымерший коралл Cyathophyllum hexagonum даже назван в честь своей шестиугольной формы, а некоторые диатомовые водоросли (основная группа водорослей) также имеют шестиугольную форму. Но, пожалуй, ни одна биологическая структура не имеет такой поразительной шестиугольной формы, как глаза стрекоз.

Глаза, состоящие примерно из 30 000 шестиугольников, переплетенных в ослепительное множество, являются одними из лучших в животном мире. Фактически, глаза стрекоз состоят из правильных шестиугольников, причем только три из этих шестиугольников встречаются в любой данной точке пересечения (или вершине).

У стрекоз два больших сложных глаза с тысячами шестиугольных линз (а также три глаза с простыми линзами, но оставим их пока в стороне). Шестиугольные линзы соединены между собой длинным тонким сетчатым каналом. На самом деле, у многих насекомых глаза имеют шестиугольную форму, и правило всегда гласит, что только три стенки клетки могут встречаться в любой вершине.

На самом деле, если мы на мгновение отойдем от биологического мира, то обнаружим, что точно такое же правило управляет чем-то совершенно другим: пеной из пузырьков.

Хотя пена пузырьков остается трудноразрешимой математической задачей, известно, что пена часто имеет тенденцию образовывать шестиугольные формы. В данном случае речь идет о поиске структуры с наименьшим общим поверхностным натяжением (что означает наименьшую площадь стены из мыльной пленки), и эта форма оказывается шестиугольником.

Конечно, структуры пены редко бывают идеально шестиугольными (а иногда они вообще не шестиугольные), потому что они также должны быть механически устойчивыми (и противостоять таким вещам, как ветер). Что еще более усложняет ситуацию, трехмерное расположение делает проблему еще более сложной. Несмотря на склонность к шестиугольникам, пена редко бывает упорядоченной.

На самом деле было удивительно много споров о том, какие формы может принимать пена, исследователи предлагали трехмерные 14-гранные многогранники и даже некоторые более безумные и беспорядочные формы. Но именно здесь становится интересно. Правила, управляющие формой ячеек в пене, похоже, также управляют некоторыми формами живых клеток. Дело не только в том, что глаза некоторых мух имеют такие же шестиугольные узоры, как и пена пузырьков, но и в том, что клетки внутри отдельных линз сгруппированы таким образом, что, похоже, повторяют геометрию пены пузырьков. Это поразительный случай, когда физика и математика направляют формы в биологическом мире.

Соединение колонн в Дороге гигантов в Северной Ирландии.

Но не вся лава остывает в одно и то же время, и некоторые участки могут все еще течь, в то время как другие уже затвердели, что может сделать формы более несовершенными. Поразительно, что часто угол удивительно близок к 120 градусам.

Если вы все еще не верите в существование шестиугольников в природе, вот еще один пример: снежинки.

Конечно, каждая снежинка уникальна, но все снежинки имеют шесть сторон или точек, и это связано с тем, как они формируются. Внешняя форма снежинок отражает их внутреннюю структуру. Гексагональная структура позволяет молекулам воды (с одним атомом кислорода и двумя атомами водорода) группироваться вместе наиболее эффективным образом.

Можете ли вы заметить шестиугольную структуру в этой снежинке?

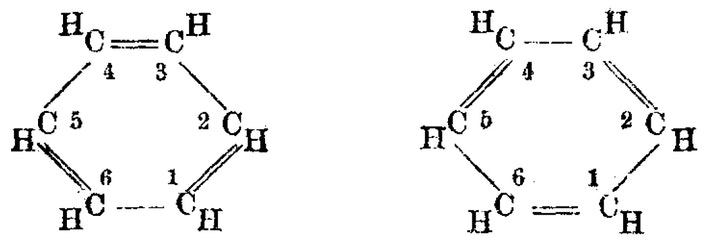
Если мы еще больше увеличим масштаб, то обнаружим еще одну форму шестиугольника. Как быстро отметит любой студент-химик, шестиугольники являются основой органической химии. Когда шесть атомов углерода соединяются, угол составляет 120 градусов, что уже должно быть знакомо. Шесть соединенных атомов углерода образуют идеальный шестиугольник, который также называется бензольным кольцом.

Есть еще один пример, который мы должны рассмотреть, и мы перейдем от очень маленьких к очень большим. Планета Сатурн имеет один из самых необычных шестиугольников в Солнечной системе: облачный узор длиной около 14 500 км; он больше, чем весь диаметр Земли. Шестиугольник состоит из газов, движущихся со скоростью 320 км/ч, и, как полагают, имеет толщину до 300 км.

Исследователи точно не знают, почему так происходит, но уже выдвинуто несколько теорий.

Почему же шестиугольники так часто встречаются в природе? Это зависит от того, как на это посмотреть. Это может быть эффективный способ сохранения массы или энергии, или просто способ расположить атомы таким образом, чтобы они были стабильны. Это может быть просто что-то, обусловленное геометрией.

Источник

Как найти периметр фигуры

Определение периметра

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра

Рассмотрим пять фигур.

Треугольник

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.

P = 3 * a, где a — длина стороны.

Квадрат и ромб

Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.

P = 4 * a, где a — длина стороны.

Прямоугольник и параллелограмм

Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.

P = 2 * (a + b), где a — ширина, b — высота.

Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!

Равнобедренная трапеция

Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.

P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Задачи на нахождение периметра и площади для 4 класса с ответами

Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:

Формулы площади и периметра для квадрата

P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата

Формулы площади и периметра для прямоугольника

P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника

Примеры решения задач разной сложности на нахождение периметра и площади

Задача 1

Каков периметр треугольника ABC?

Ответ: периметр треугольника равен 125 см.

Задача 2

Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?

Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.

Задача 3

Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?

Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.

Задача 4

У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?

Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.

Задача 5

В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?

Ответ: Периметр прямоугольника равен 60 см.

Задача 6

Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?

Ответ: Площадь прямоугольника 56 м².

Задача 7

Площадь витрины квадратной формы 64м². Узнай ее периметр.

Ответ: Периметр витрины равен 32 м.

Задача 8

Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.

Ответ: Площадь прямоугольника равна 630 см².

Задача 9

Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?

Ответ: 42 дерева.

Задача 10

Каков периметр синей фигуры?

Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.

Задача 11

Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?

Ответ: Длина второго участка 40 м.

Задача 12

Найди периметр квадрата со стороной 8 см.

Ответ: Периметр квадрата 32 см.

Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.

Решение:

120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)

Ответ: Периметр бассейна 46 метров

Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.

Решение:

8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)

Ответ: Периметр прямоугольника 16 см.

Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?

Решение:

5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)

Ответ: Ученик ошибся на 3 см²

Ответ: Ширина другого участка 24 м.

У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?

Ответ: Площадь квадрата больше на 4 см.

Задача 20

Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.

У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.

Задача 22

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?

1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36

Ответ: Незабудками засажено 36 м².

Задача 23

Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18

Ответ: Площадь прямоугольника 18 м².

Задача 24

Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?

1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см

Ответ: Периметр стола 280 см.

Задача 25

Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?

1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75

Ответ: Площадь прямоугольника 75 см².

Площадь квадрата 49 кВ дм. Узнайте его периметр.

1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)

Ответ: Периметр квадрата равен 28 дм.

Задача 27

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32

Ответ: Площадь окна равна 32 м².

Задача 28

Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?

1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152

Ответ: Капустой засадили 1152 м².

Найди периметр квадрата со стороной 16 см.

Ответ: Периметр квадрата 64 см.

Задача 30

Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.

(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13

Ответ: Длина прямоугольника 13 см.

Задача 31

Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.

Ответ: Ширина прямоугольника 5 см.

Задача 32

Периметр квадрата 24 см. Найди его площадь.

24 : 4 = 6 (см)
6 · 6 = 36 (см²)

Ответ: Площадь квадрата 36 см².

Задача 33

Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.

Ответ: Площадь прямоугольника 56 см².

Задача 34

Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?

40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)

Ответ: Периметр прямоугольника 28 см.

Задача 35

Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.

Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.

У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).

Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)

Ответ: Площадь всех граней куба равна 24 см².

Задача 36

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Ответ: Площадь получившейся фигуры равна 44.

Задача 37

Площадь одной клетки равна 1см.

Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².

Задача 38

Найдите площади и периметры фигурок. Сделайте вывод.

Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²

Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.

Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.

Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.

Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.

Задача 39

Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?

Ответ: Периметр красной фигуры равен 27 см.

Задача 40

Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?

Ответ: Периметр равен 36 см.

Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?

Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.

Задача 42

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.

Ответ: Периметр прямоугольника равен 24 см.

Задача 43

Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?

Ответ: Расстояние пройденное улиткой будет равно 28 см.

Задача 44

В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?

Задача 45

Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?

Ответ: Периметр зеленой зоны равен 100 метров.

Источник

Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями

Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Простейшие четырёхугольники

Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.

Наиболее часто приходится сталкиваться со следующими видами:

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.

Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.

Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Треугольный многоугольник

Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.

В зависимости от особенностей, фигура может называться:

Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.

Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.

Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.

Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Теорема об углах

Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.

Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

Источник