Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Параллелограмм. Свойства и признаки параллелограмма

Определение параллелограмма

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма

1. Противоположные стороны параллелограмма попарно равны

2. Противоположные углы параллелограмма попарно равны

3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов

4. Сумма всех углов равна 360°

5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

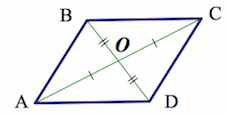
6. Точка пересечения диагоналей является центром симметрии параллелограмма

7. Диагонали параллелограмма и стороны
связаны следующим соотношением:

8. Биссектриса отсекает от параллелограмма равнобедренный треугольник

Признаки параллелограмма

Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Противоположные стороны попарно равны:

2. Противоположные углы попарно равны:

3. Диагонали пересекаются и в точке пересечения делятся пополам

4. Противоположные стороны равны и параллельны:

5.

Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:

Формулы площади параллелограмма смотрите здесь.

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.

Источник

Параллелограмм: свойства и признаки

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

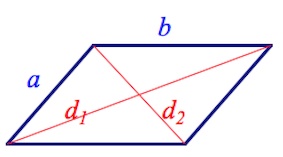
Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Как найти площадь параллелограмма:

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные занятия по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Четырехугольники

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Виды четырёхугольников

Параллелограмм

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма

d 1 2 +d 2 2 =2(a 2 +b 2 ).

Признаки параллелограмма

Четырехугольник является параллелограммом, если:

Трапеция

Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны.

Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.

Трапеция называется равнобедренной (или равнобокой ), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства трапеции

Признаки трапеции

Четырехугольник является трапецией, если его параллельные стороны не равны

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Признаки прямоугольника

Параллелограмм является прямоугольником, если:

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба

Признаки ромба

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства квадрата

Признаки квадрата

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

Основные формулы

Источник

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

S=ab, где a и b соседние стороны прямоугольника.

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

pазбирался: Даниил Романович | обсудить разбор | оценить

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

pазбирался: Даниил Романович | обсудить разбор | оценить

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Для выполнения данного задания надо подставить все известные данные в формулу:

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объекты	яблони	теплица	сарай	жилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объекты	яблони	теплица	сарай	жилой дом
Цифры	3	5	1	7

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина	Расход краски	Масса краски в одной банке	Стоимость одной банки краски	Стоимость доставки заказа
1	0,25 кг/кв.м	6 кг	3000 руб.	500 руб.
2	0,4 кг/кв.м	5 кг	1900 руб.	800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник