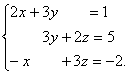угол образован векторами и найдите какой нибудь вектор биссектрисы этого угла

Пример 4. Найти вектор а, коллинеарный вектору с = 3i — 6j + 2k, составляющий с осью Ох тупой угол, если |a| = 14.

Решение. Искать вектор а будем исходя из формулы a = |a| a₀. Так как вектор a коллинеарен вектору c и образует тупой угол с осью Ох, а вектор c образует острый угол с осью Ох

Пример 5. Найти вектор с, направленный по биссектрисе угла, образованного векторами

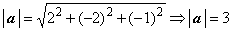
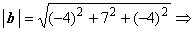
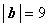
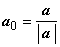
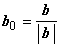
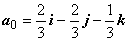
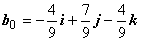
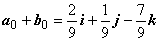
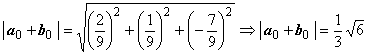
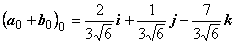
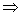
Решение. Чтобы вектор c был направлен по биссектрисе, он должен быть диагональю ромба. Найдём модули векторов: и и орты и : и . Тогда вектор направлен по биссектрисе. Найдем модуль вектора a₀ + b₀: и орт . Находим вектор с = |с| (a₀ + b₀) c = 2 i + j – 7 k.

Задачи для самостоятельной работы.

7. Разложить вектор d = 2 i – 6 j по векторам , , .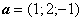

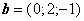
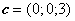
Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Определить координаты вектора с, направленного по биссектрисе угла между векторами а и b

Помогите с решением этой довольно распространенной задачи.

Два вектора а = <2; — 3; 6> и b = <— 1; 2; —2> приложены к одной точке. Определить координаты вектора с, направленного по биссектрисе угла между векторами а и b, при условии, что длина вектора c= оо

P.S. Не обязательно само решение, достаточно будет пару дельных советов или подсказок по решению.

Найти проекцию вектора, имеющего некоторую длину и направленного по биссектрисе угла
Здравствуйте! Объясните, пожалуйста, алгоритм решения подобных задач: Найти проекцию вектора A.

Заданы два вектора. Определить угол между векторами
№1 Вычисления в математических задачах Заданы два вектора с координатами (X1, Y1, Z1) и (X2, Y2.

Определить вектор, коллинеарный биссектрисе угла треугольника
Определить вектор, коллинеарный биссектрисе угла A треугольника ABC, если А(1,3,5) B(3,5,6).

Решение

Указание к решению задачи:

1) Найдите координаты единичных векторов e_a и e_b сонаправленных с векторами a и b соответственно.
2) Суммарный вектор e_a + e_b будет направлен по биссектрисе угла между векторами a и b.
3) Зная координаты вектора e_a + e_b, найдите сонаправленный с ним единичный вектор e_c.
4) «Растяните» вектор e_c на длину вектора c, тогда получится вектор с.

Источник

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Решение

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Решение

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Решение

и отсюда выведем формулу косинуса угла:

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Источник

3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

При умножении вектора на число все его координаты

Умножаются на это число, при сложении векторов складываются их соответствующие координаты.

Координаты коллинеарных векторов пропорциональны.

Если A || B, то . Отсюда:

Ответ: .

Направляющие косинусы являются координатами орта (единичного вектора) данного направления.

Найдем модуль вектора А:

Разделив все координаты вектора А на его модуль, получим координаты орта:

Ответ:

Система векторов называется линейно независимой, если равенство

Вычислим главный определитель Δ системы уравнений

По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).

Поскольку других решений нет, данная система векторов линейно независима.

Ответ: Система векторов линейно независима.

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Найдем координаты этих векторов:

Из последней пропорции получаем, что Z = 1 – 2Y. Тогда

Но при этих значениях неизвестных

Условие задачи выполнено.

Используйте определение скалярного произведения:

Используем свойства скалярного произведения:

По определению скалярного произведения

Сложим левые и правые части полученных равенств:

Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.

Используем свойства скалярного произведения:

Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.

Ответ: .

Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Ответ: K = .

Используйте свойство направляющих косинусов:

Найдем cosγ: cos260o + cos245o + cos2γ = 1,

Тогда проекция А на заданную ось равна:

Источник

Задачник «Векторный метод решения задач»

Ищем педагогов в команду «Инфоурок»

Задачник «Векторный метод решения задач»

Составила: Казакова Ольга Сергеевна,

учитель математики МОУ «СОШ № 75» г. Саратова.

Данный задачник предназначен для изучения тем: «Векторы», «Действия с векторами», «Векторный метод решения задач». Инструктивное изложение материала, при постоянной практической пробе, даёт возможность изучить темы самостоятельно.

№ 1.Заполните таблицу. Основные понятия.

Решение и изображение

3)Построен вектор , его можно обозначить и однострочной латинской буквой, например, , которая записывается над изображением вектора.

Сколько векторов можно провести, выбирая начало и конец среди данных на плоскости:

2)трёх точек, не лежащих на одной прямой;

3)четырёх точек, не лежащих на одной прямой?

Обозначение нулевого вектора: или символом .

2)Постройте вектор .

Обозначение: = AB = 4.

Чему равна длина нулевого вектора?

3)Постройте вектор , длиной 7 см.

2)На прямой p постройте:

а)вектор , произвольной длины и направления;

б)вектор , произвольной длины и направления;

3)На прямой m постройте: вектор , произвольной длины и направления.

Нулевой вектор считается коллинеарным любому вектору.

4)Выпишите попарно коллинеарные векторы.

5)Постройте и обозначьте два произвольных вектора, которые являются не коллинеарными вектору . Будут ли они являться коллинеарными векторам , ?

Постройте два коллинеарных вектора.

Полученные векторы направлены одинаково или противоположно?

Если одинаково, то вы построили сонаправленные векторы. Обозначение:

 .

Если противоположно, то вы построили противоположно направленные векторы. Обозначение:  .

1)коллинеарными друг другу;

Постройте векторы и , так, чтобы:

1)  ;

2) .

Вы построили равные векторы.

№ 2.Заполните таблицу. Операции над векторами.

Решение и изображение

Можно отложить от другой точки плоскости, вектор, равный данному вектору ?

Допустим, что вектор ненулевой, а точки A и B – его начало и конец.

Среди построенных векторов выберите тот, что сонаправлен с вектором , он и будет являться искомым вектором, равным вектору . К тому же такой вектор только один, что следует из построения.

А если вектор – нулевой? Ответьте самостоятельно.

Итак, от любой точки M можно отложить вектор, равный данному вектору , и при том только один.

1)Векторы и .

3)От точки A отложите вектор , равный вектору .

4)От точки B отложите вектор , равный вектору .

5)Вектор .

Докажем, что если и , то .

а) ;

б) ;

в)Соединим точки A и , B и , C и ;

2)  – параллелограмм  ;

3)  – параллелограмм  ;

4)Из 2) и 3)   – параллелограмм;

5)Значит, . Доказано.

Вывод: при необходимости можно работать как с данными векторами, так и с равными им.

Законы сложения векторов.

Для любых векторов , и справедливы равенства:

(переместительный закон)

(сочетательный закон)

Доказательство законов проведите самостоятельно, опираясь на подсказки:

Для доказательства первого закона можете достроить треугольник до параллелограмма и работать как с самими векторами, так и с равными им.

Для доказательства второго закона достаточно несколько раз применить правило треугольника для сложения векторов, последовательно отложенных от концов предыдущих векторов.

1)Произвольная точка A ;

2)Неколлинеарные векторы и ;

3) От точки A отложите вектор , равный вектору .

4)От точки A отложите вектор , равный вектору .

5)Постройте параллелограмм ABCD ;

6) .

Вы построили сложение векторов и по правилу параллелограмма сложения неколлинеарных векторов.

Как сложить несколько векторов?

Последовательное применение правила треугольника для сложения векторов даёт возможность сложить любое количество векторов. Причём порядок сложения не важен. Сложение нескольких векторов производится следующим образом: два вектора складываются, получившаяся сумма складывается с третьим и т.д.

Выполните сложение пяти любых векторов, используя то, что несколько векторов можно расположить таким образом: первый вектор откладывается от любой точки, второй – от конца первого и т.д. Сумма всех векторов – вектор, направленный от начала первого вектора к концу последнего.

Подумайте, чему будет равна сумма векторов, если начало первого вектора совпадает с концом последнего?

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены. Обозначение: . .

Докажите, что . Для этого воспользуйтесь определением разности векторов и прибавлением к обеим частям равенства вектора.

На прямой p от любой точки O отложите вектор , от конца вектора отложите вектор . Длина построенного суммарного вектора, равна или .

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причём векторы и сонаправлены при k  0 и противоположно направлены при k .

Произведением нулевого вектора на любое число считается нулевой вектор.

Из определения следует:

1)произведение любого вектора на число нуль есть нулевой вектор;

2)для любого числа k и любого вектора векторы и коллинеарны.

Свойства умножения вектора на число.

(сочетательный закон)

(первый распределительный закон)

(второй распределительный закон)

На прямой p от произвольно выбранной точки O отложите: вектор , длиной 1 см; вектор , сонаправленный с вектором , длиной 2 см; вектор , противоположно направленный с вектором , длиной 3 см.

Попробуем выразить векторы и через вектор .

Во сколько раз длины этих векторов отличаются от длины вектора ?

; ;

 ,  , т. е. векторы , и коллинеарны друг другу, значит, можно воспользоваться леммой.

Если векторы и коллинеарны и , то существует такое число k , что .

Итак, можем выразить: , .

Если  , то

Если , то векторы и называются перпендикулярными.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Напишите формулу скалярного произведения для случаев, когда:

;

;

.

Сделайте вывод, о том, в каком случае скалярное произведение двух векторов равно нулю.

Итак, перечислите все операции над векторами.

№ 3.Решая задачи, заполните пустые ячейки в таблице.

точки M и N совпадают

точка C принадлежит прямой AB

, или
, или

точка С – середина отрезка AB

точка D разбивает отрезок AC так, что AD : DC = m : n

Заполняя таблицу, вы пользовались векторным методом решения задач.

Векторный метод – один из наиболее общих методов решения геометрических задач.

Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.

Далее вам необходимо самостоятельно решать задачи. После решения каждой задачи делайте вывод о её значимости. Если результат задачи возможно использовать для решения других, то заносите его в таблицу № 3. Таким образом, вы получите набор базовых задач, на основании которых решаются более сложные.

1)Докажите, что средняя линия треугольника параллельна его третьей стороне и равна её половине.

2)Докажите, что средняя линия трапеции параллельна её основанию и её длина равна полусумме длин её оснований.

3)Если средняя линия четырёхугольника равна полусумме длин её оснований (сторон, не имеющих общей точки со средней линией), то этот четырёхугольник является трапецией или параллелограммом.

5)Докажите, что биссектриса угла треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам. Выразите биссектрису через угол треугольника, который она делит пополам, и через стороны этого угла.

7)В треугольнике ABC через M обозначена точка пересечения медиан. Докажите, что .

11)Докажите, что центр описанной окружности

12)Докажите, что если точки пересечения диагоналей четырёхугольника и середины двух его противоположных сторон лежат на одной прямой, то этот четырёхугольник – трапеция или параллелограмм.

13)Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

14)Докажите, что биссектрисы треугольника пересекаются в одной точке.

15)Докажите, что высоты треугольника пересекаются в одной точке.

16)Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда его диагонали в точке пересечения делятся пополам.

17)Докажите, что в произвольном четырёхугольнике средние линии (т. е. отрезки, соединяющие середины противоположных сторон) точкой их пересечения делятся пополам.

19)Докажите, что диагонали ромба взаимно перпендикулярны.

25)Докажите, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.

26)Докажите, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин её боковых сторон плюс удвоенное произведение длин оснований.

27)Доказать, что большей медиане треугольника соответствует меньшая сторона и обратно.

28)Докажите, диагонали прямоугольника равны между собой.

29)Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.

45)Докажите, что точки пересечения диагоналей трапеции, боковых сторон, а также середины оснований лежат на одной прямой.

49)Докажите, что прямая, соединяющая середины оснований трапеции, и продолжения боковых сторон трапеции пересекаются в одной точке.

50)На сторонах параллелограмма заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки деления служат вершинами параллелограмма, а центры этих параллелограммов совпадают.

51)На сторонах треугольника заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки пересечения медиан данного треугольника и треугольника, имеющего вершинами точки деления, совпадают.

53)Найдите косинус угла между медианами прямоугольного равнобедренного треугольника, проведёнными к его катетам.

54)Найти косинус угла между медианами равнобедренного треугольника, проведёнными к его боковым сторонам, при условии, что угол при вершине равен α.

55)Найти косинус угла при вершине равнобедренного треугольника, если медианы, проведённые к его боковым сторонам, а) перпендикулярны; б) образую угол .

56)В треугольнике две стороны равны 2 и 4, а угол между ними равен . Найти угол ψ между короткой стороной и медианой, проведённой к третьей стороне.

Список использованной литературы

Атанасян Л.С. и др. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2003.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2009.

Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Шестаков С.А., Юдина И.И. Планиметрия. Пособие для углубленного изучения математики – М.: ФИЗМАТЛИТ, 2005.

Василевский А.Б. Методы решения геометрических задач. – Минск: Вышэйш. школа, 1965.

Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996.

Гордин Р.К. Геометрия. Планиметрия 7-9 кл. – М.: МЦНМО, 2006.

Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 кл. – М.: Просвещение, 1979.

Гусев В. А. и др. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей. – М.: Просвещение, 1992.

Зеленяк О. П. Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Моделирование в среде Turbo Pascal. – Киев, Москва: ДиаСофтЮП, ДМК Пресс, 2008.

Шарыгин И. Ф. Геометрия. 7 – 9 кл.: Учеб. для общеобразоват. учеб. завед. – М.: Дрофа, 2001.

Шарыгин И.Ф. Решение задач: Учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.

Шестаков С. А. Векторы на экзаменах. Векторный метод в стереометрии. – М.: МЦНМО, 2005.

Источник