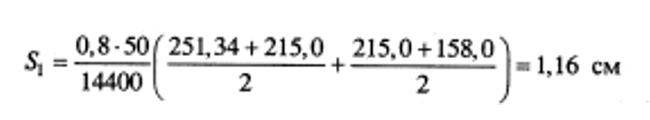укажите какие напряжения учитываются при расчете осадки методом послойного суммирования
5.5.4. Расчет деформаций основания (ч. 1)
А. ОСАДКИ ФУНДАМЕНТОВ
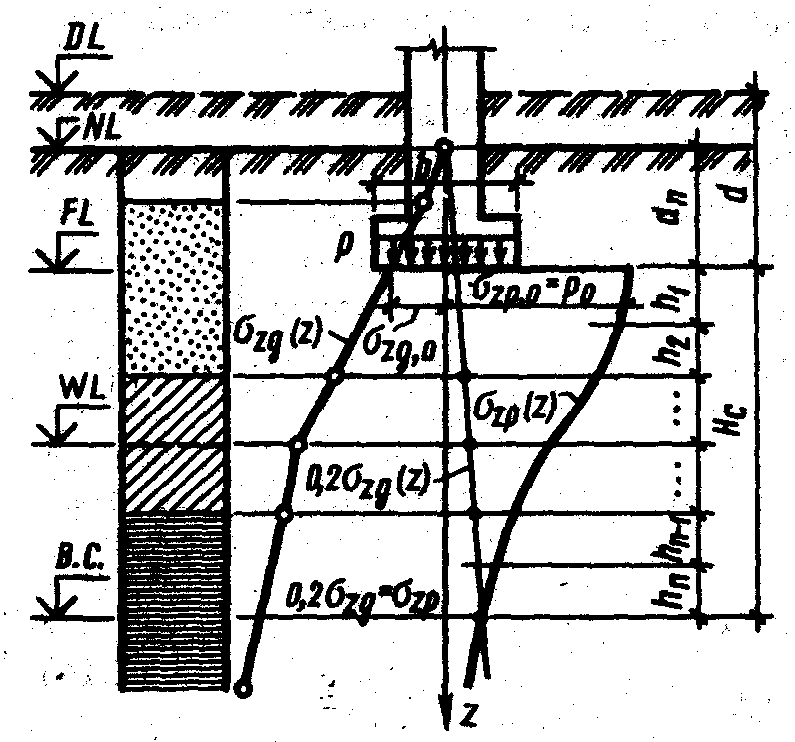
Определение осадки методом послойного суммирования. В методе послойного суммирования приняты следующие допущения:
Осадка основания s методом послойного суммирования определяется по формуле
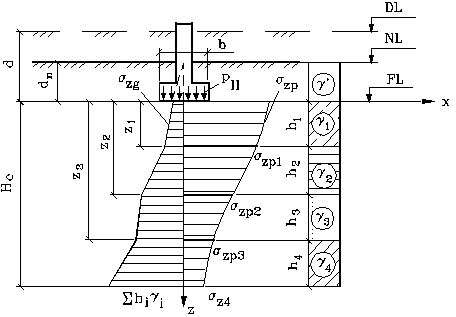
При этом распределение вертикальных нормальных напряжений по глубине основания принимается в соответствии со схемой, приведенной на рис. 5.26.
Дополнительные вертикальные нормальные напряжения по вертикали, проходящей через центр рассматриваемого фундамента, на глубине z от его подошвы определяются:
Суммарное дополнительное напряжение по оси рассчитываемого фундамента с учетом влияния нагрузок от соседних фундаментов определяется по формуле (5.19).
Пример 5.12. Рассчитать осадку фундамента Ф-1 здания с гибкой конструктивной схемой с учетом влияния нагрузки на фундамент Ф-2 по условиям примера 5.2 (см. рис. 5.11) при следующих данных. С поверхности до глубины h + h1 = 6 м залегает песок пылеватый со следующими характеристиками, принятыми по справочным таблицам (см. гл. 1): γs = 26,6 кН/м 3 ; γ = 17,8 кН/м 3 ; ω = 0,14; е = 0,67; сII = 4 кПа; φII = 30°; E = 18 000 кПа. Ниже залегает песок мелкий с характеристиками: γs = 26,6 кН/м 3 ; γ = 19,9 кН/м 3 ; ω = 0,21; е = 0,62; сII = 2 кПа; φII = 32°; E = 28 000 кПа. Уровень подземных вод находится на глубине 6,8 м от поверхности. Суммарная нагрузка на основание от каждого фундамента (с учетом его веса) N = 5,4 МН.
Решение. По формуле (5.21) удельный вес песка мелкого с учетом взвешивающего действия воды
По табл. 5.11 находим: γc1 = 1,2 и γc2 = 1. По табл. 5.12 при φII = 30° находим: Mγ = 1,15; Мq = 5,59; Мc = 7,95. Поскольку характеристики грунта приняты по таблицам, k = 1,1.
По формуле (5.29) получаем:

Среднее давление под подошвой
р = 5400/4 2 = 338 кПа R = 341 кПа;
дополнительное давление на основание
Дополнительные вертикальные нормальные напряжения в основании фундаментов Ф-1 и Ф-2 подсчитаны в примере 5.2, приведены в табл. 5.6 и показаны на рис. 5.11. Дополняем табл. 5.6 подсчетом напряжений от собственного веса грунтов σzg для определения нижней границы сжимаемой толщи (табл. 5.16).
Из табл. 5.16 видно, что нижняя граница сжимаемой толщи под фундаментом Ф-1 находится на глубине z1 = 8,0 м (при учете нагрузки только на этот фундамент) и на глубине z2 = 8,8 м (при учете влияния фундамента Ф-2).
ТАБЛИЦА 5.16. К ПРИМЕРУ 5.12
Примечание. Значения напряжений и модуля даны в кПа.
Определяем осадку фундамента Ф-1 по формуле (5.60):
без учета влияния Ф-2

с учетом влияния Ф-2

Определение осадки основания с использованием схемы линейно-деформируемого слоя.
Средняя осадка фундамента на слое конечной толщины (рис. 5.27) определяется по формуле [4]
Формула (5.61) служит для определения средней осадки основания, загруженного равномерно распределенной по ограниченной площади нагрузкой. Эту формулу допускается применять для определения осадки жестких фундаментов.
ТАБЛИЦА 5.17. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА kc
| Относительная толщина слоя ζ´ = 2H/b | kс |
| 0 ζ´ ≤ 0,5 | 1,5 |
| 0,5 ζ´ ≤ l | 1,4 |
| 1 ζ´ ≤ 2 | 1,3 |
| 2 ζ´ ≤ 3 | 1,2 |
| 3 ζ´ ≤ 5 | 1,1 |
| ζ´ > 5 | 1,0 |
ТАБЛИЦА 5.18. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА km
Расчетная толщина линейно-деформируемого слоя H (см. рис. 6.27) принимается до кровли малосжимаемого грунта (см. п. 5.1), а при ширине (диаметре) фундамента b > 10 м и среднем значении модуля деформации грунтов основания E > 10 МПа вычисляется по формуле
где H0 и ψ — принимаются соответственно равными для оснований, сложенных пылевато-глинистыми грунтами 9 м и 0,15, а сложенных песчаными грунтами 6 м и 0,1; kp — коэффициент, принимаемый; kp = 0,8 при среднем давлении под подошвой фундамента p = 100 кПа; kp = 1,2 при р = 500 кПа; при промежуточных значениях — по интерполяции.
Если основание сложено и пылевато-глинистыми, и песчаными грунтами, значение Н определяется по формуле
ТАБЛИЦА 5.19. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА k
| ζ = 2z/b | k для фундаментов | |||||||
| круглых | прямоугольных с соотношением сторон η = l/b | ленточных ( η ≥ 10) | ||||||
| 1 | 1,4 | 1,8 | 2,4 | 3,2 | 5 | |||
| 0,0 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,4 | 0,090 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,104 |
| 0,8 | 0,179 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,208 |
| 1,2 | 0,266 | 0,299 | 0,300 | 0,300 | 0,300 | 0,300 | 0,300 | 0,311 |
| 1,6 | 0,348 | 0,380 | 0,394 | 0,397 | 0,397 | 0,397 | 0,397 | 0,412 |
| 2,0 | 0,411 | 0,446 | 0,472 | 0,482 | 0,486 | 0,486 | 0,486 | 0,511 |
| 2,4 | 0,461 | 0,499 | 0,538 | 0,556 | 0,565 | 0,567 | 0,567 | 0,605 |
| 2,8 | 0,501 | 0,542 | 0,592 | 0,618 | 0,635 | 0,640 | 0,640 | 0,687 |
| 3,2 | 0,532 | 0,577 | 0,637 | 0,671 | 0,696 | 0,707 | 0,709 | 0,763 |
| 3,6 | 0,558 | 0,606 | 0,676 | 0,717 | 0,750 | 0,768 | 0,772 | 0,831 |
| 4,0 | 0,579 | 0,630 | 0,708 | 0,756 | 0,796 | 0,820 | 0,830 | 0,892 |
| 4,4 | 0,596 | 0,650 | 0,735 | 0,789 | 0,837 | 0,867 | 0,883 | 0,949 |
| 4,8 | 0,611 | 0,668 | 0,759 | 0,819 | 0,873 | 0,908 | 0,932 | 1,001 |
| 5,2 | 0,624 | 0,683 | 0,780 | 0,834 | 0,904 | 0,948 | 0,977 | 1,050 |
| 5,6 | 0,635 | 0,697 | 0,798 | 0,867 | 0,933 | 0,981 | 1,018 | 1,095 |
| 6,0 | 0,645 | 0,708 | 0,814 | 0,887 | 0,958 | 1,011 | 1,056 | 1,138 |
| 6,4 | 0,653 | 0,719 | 0,828 | 0,904 | 0,980 | 1,031 | 1,090 | 1,178 |
| 6,8 | 0,661 | 0,728 | 0,841 | 0,920 | 1,000 | 1,065 | 1,122 | 1,215 |
| 7,2 | 0,668 | 0,736 | 0,852 | 0,935 | 1,019 | 1,088 | 1,152 | 1,251 |
| 7,6 | 0,674 | 0,744 | 0,863 | 0,948 | 1,036 | 1,109 | 1,180 | 1,285 |
| 8,0 | 0,679 | 0,751 | 0,872 | 0,960 | 1,051 | 1,128 | 1,205 | 1,316 |
| 8,4 | 0,684 | 0,757 | 0,881 | 0,970 | 1,065 | 1,146 | 1,229 | 1,347 |
| 8,8 | 0,689 | 0,762 | 0,888 | 0,980 | 1,078 | 1,162 | 1,251 | 1,376 |
| 9,2 | 0,693 | 0,768 | 0,896 | 0,989 | 1,089 | 1,178 | 1,272 | 1,404 |
| 9,6 | 0,697 | 0,772 | 0,902 | 0,998 | 1,100 | 1,192 | 1,291 | 1,431 |
| 10,0 | 0,700 | 0,777 | 0,908 | 1,005 | 1,110 | 1,205 | 1,309 | 1,456 |
| 11,0 | 0,705 | 0,786 | 0,922 | 1,022 | 1,132 | 1,233 | 1,349 | 1,506 |
| 12,0 | 0,710 | 0,794 | 0,933 | 1,037 | 1,151 | 1,257 | 1,384 | 1,550 |
Примечание. При промежуточных значениях ζ и η коэффициент k определяется по интерполяции.
Решение. Расчетную толщину слои определяем но формуле (5.62) для двух случаев: основание сложено только песчаными и только пылевато-глинистыми грунтами (при р = 0,3 МПа коэффициент kр = 1):
Тогда по формуле (5.63)
H = 8 + 7/3 = 10,3 м ≈ 10 м.
При ζ´ = 2 · 10/20 = 1 по табл. 5.17 kc = 1,4; при Е > 10 МПа и b > 15 м по табл. 5.18 коэффициент km = 1,5.
Определяем коэффициенты ki по табл. 5.19, учитывая, что η = 100/20 = 5:
Тогда по формуле (5.61)

Осадки центра, середин сторон и угловых точек прямоугольной площади размером b×l при действии на нее равномерного давления р определяются по формуле [2]:
где E — модуль деформации грунта основания, принимаемый средним в пределах сжимаемой толщи; k´ = k0 коэффициент, принимаемый по табл. 5.20 для центра прямоугольника; k´ = k1 — то же, для середины большей стороны; k´ = k2 — то же, для середины меньшей стороны; k´ = k3 — то же, для угловой точки.
Осадки поверхности основания при действии на него равномерного давления р по круглой площадке радиусом r на расстоянии R от центра этой площадки также можно определить по формуле (5.64), в которой коэффициент k´ = kr принимается по табл. 5.21 [2]. Указанным способом допускается определять осадки поверхности основания за пределами жесткого круглого фундамента.
Влияние на осадку рассчитываемого фундамента других фундаментов, нагрузок на полы и т.п. может быть оценено по формуле (5.64) с использованием схемы фиктивных фундаментов аналогично определению напряжений в основании методом угловых точек либо с помощью ЭВМ по стандартной программе. Дополнительную осадку рассчитываемого фундамента от влияния других фундаментов допускается принимать равной дополнительной осадке его центра.
ТАБЛИЦА 5.20. ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ k0, k1, k2, k3
| η | ζ´ = 2H/b | k0 | k1 | k2 | k3 | η | ζ´ = 2H/b | k0 | k1 | k2 | k3 |
| 1 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,236 0,464 0,701 0,801 0,892 0,928 0,955 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,024 0,056 0,115 0,231 0,305 0,380 0,416 0,444 | 3 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,019 1,238 1,338 1,420 | 0,045 0,109 0,227 0,464 0,655 0,855 0,955 1,037 | 0,045 0,107 0,225 0,400 0,510 0,656 0,742 0,815 | 0,024 0,056 0,115 0,231 0,325 0,460 0,545 0,617 |
| 1,5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,773 0,910 1,037 1,092 1,137 | 0,045 0,109 0,236 0,446 0,564 0,682 0,737 0,783 | 0,045 0,108 0,231 0,404 0,508 0,617 0,669 0,712 | 0,024 0,056 0,115 0,231 0,323 0,426 0,478 0,518 | 5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,454 0,801 1,028 1,310 1,456 1,592 | 0,045 0,109 0,227 0,464 0,655 0,919 1,065 1,192 | 0,045 0,107 0,225 0,400 0,511 0,656 0,752 0,852 | 0,024 0,056 0,115 0,231 0,326 0,462 0,555 0,652 |
| 2 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,792 0,974 1,128 1,201 1,265 | 0,045 0,109 0,227 0,464 0,610 0,755 0,837 0,883 | 0,044 0,107 0,225 0,403 0,514 0,641 0,708 0,762 | 0,024 0,056 0,115 0,231 0,324 0,448 0,512 0,565 | 10 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,028 1,319 1,492 1,702 | 0,045 0,109 0,227 0,464 0,655 0,928 1,110 1,310 | 0,045 0,107 0,225 0,400 0,511 0,658 0,756 0,858 | 0,024 0,056 0,115 0,231 0,326 0,463 0,558 0,659 |
ТАБЛИЦА 5.21. ЗНАЧЕНИЕ КОЭФФИЦИЕНТА kr
| ζ´ = H/r | kr при ρ = R/r | |||||||||||
| 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,25 | 0,12 | 0,12 | 0,12 | 0,12 | 0,05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,5 | 0,24 | 0,24 | 0,23 | 0,22 | 0,11 | 0,01 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,75 | 0,35 | 0,35 | 0,34 | 0,29 | 0,16 | 0,03 | 0,01 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,45 | 0,44 | 0,42 | 0,35 | 0,21 | 0,07 | 0,02 | 0 | 0 | 0 | 0 | 0 |
| 1,5 | 0,58 | 0,57 | 0,53 | 0,45 | 0,28 | 0,13 | 0,07 | 0,02 | 0 | 0 | 0 | 0 |
| 2 | 0,65 | 0,64 | 0,60 | 0,52 | 0,34 | 0,17 | 0,10 | 0,04 | 0,01 | 0 | 0 | 0 |
| 3 | 0,74 | 0,73 | 0,68 | 0,59 | 0,41 | 0,23 | 0,16 | 0,08 | 0,04 | 0,02 | 0 | 0 |
| 5 | 0,81 | 0,79 | 0,74 | 0,66 | 0,47 | 0,30 | 0,22 | 0,13 | 0,09 | 0,06 | 0,02 | 0,01 |
| 7 | 0,84 | 0,82 | 0,77 | 0,69 | 0,50 | 0,33 | 0,24 | 0,15 | 0,11 | 0,08 | 0,04 | 0,02 |
| 10 | 0,85 | 0,83 | 0,79 | 0,71 | 0,52 | 0,35 | 0,27 | 0,18 | 0,13 | 0,10 | 0,06 | 0,04 |
| ∞ | 0,91 | 0,89 | 0,84 | 0,76 | 0,58 | 0,40 | 0,32 | 0,23 | 0,18 | 0,15 | 0,11 | 0,09 |
ТАБЛИЦА 5.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ω
| Форма загруженной площади | η | ω для определения | |||
| осадки равномерно загруженной площади | осадки абсолютно жесткого фундамента ωconst | ||||
| в угловой точке ωc | в центре ω0 | в средней ωm | |||
| Прямоугольная | 1 | 0,5 ω0 | 1,12 | 0,95 | 0,88 |
| 1,5 | 1,36 | 1,15 | 1,08 | ||
| 2 | 1,53 | 1,30 | 1,22 | ||
| 3 | 1,78 | 1,53 | 1,44 | ||
| 4 | 1,96 | 1,70 | 1,61 | ||
| 5 | 2,10 | 1,83 | 1,72 | ||
| 6 | 2,23 | 1,96 | 1,83 | ||
| 7 | 2,33 | 2,04 | 1,92 | ||
| 8 | 2,42 | 2,12 | 2,00 | ||
| 9 | 2,49 | 2.19 | 2,06 | ||
| 10 | 2,53 | 2,25 | 2,12 | ||
| Круглая | – | 0,64 | 1,00 | 0,85 | 0,79 |
Определение осадки путем непосредственного применения теории линейно-деформируемой среды. Для предварительной оценки осадок фундаментов допускается пользоваться формулой
где ω — коэффициент, принимаемый по табл. 5.22; v — коэффициент Пуассона.
Во всех случаях формула (5.65) приводит к преувеличению расчетных осадок (по сравнению с методами, рекомендуемыми нормами). Достаточно удовлетворительные результаты эта формула дает при ширине фундамента b η = l/b
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Порядок расчета осадки фундаментов
Осадка фундамента
Вы здесь: Реконструкция деревянного дома =>Основания и фундаменты =>Пример расчета основания =>Осадка фундамента
Пример расчета
Ниже, в качестве примера, приведен расчет осадки основания фундамента реконструируемого деревянного дома. (см. описание фундамента и грунтовые условия на площадке строительства см. столбчатый фундамент на песчаной подушке).
Решение
Осадку основания фундамента s, см, с использованием расчетной схемы в виде линейно деформируемого полупространства (см. п. 5.6.31) определяют методом послойного суммирования по формуле (5.16 )
s = β∑ni=1 (σzp,I — σγ,i)hi / Ei + β∑ni=1 σzγ,Ihi / Eв,i (5.16)
γ’ =(γ’1h1 +γ’2h2)/(h1+h2) = (12,0×0,2 + 18,4×0,4) / (0,2×0,4) = 1,63 кН / м3
σzg,0 = γ’d = 18,4 кН/м3 × 0,6 м = 11,6 кПа.
По формуле (5.8) определяем величены напряжений σzg,i в элементарных слоях от собсвенного веса вышележажих слоев грунта и от внешней нагрузки σzp,i на глубине z. Нижняя границы сжимаемой толщи основания Hс определяется графическим способом как ордината точка пересечения кривой σzp с прямой 0,5σzg. Для упрощения расчета пренебрегаем снижением напряжений от собсвенного веса вынутого в котловане грунта. Результаты расчета приведены в нижеледующей таблице.
| z, м | ξ | α(η=1,8) | α(η=2,4) | α(η=2,0) | σzp,кПа | σzp,ср,кПа | σzg,кПа | σzg,ср,кПа | 0,5σzg,ср,кПа | s, см |
| 1 | 1 | 1 | 100,30 | 99,06 | 9,76 | 9,95 | 4,97 | 0,02 | ||
| 0,04 | 0,4 | 0,975 | 0,976 | 0,975 | 97,82 | 92,51 | 10,52 | 10,89 | 5,45 | 0,02 |
| 0,08 | 0,8 | 0,866 | 0,876 | 0,869 | 87,19 | 79,92 | 12,03 | 12,60 | 6,30 | 0,02 |
| 0,12 | 1,2 | 0,717 | 0,739 | 0,724 | 72,65 | 65,88 | 14,30 | 15,05 | 9,13 | 0,01 |
| 0,16 | 1,6 | 0,578 | 0,612 | 0,589 | 59,11 | 53,47 | 17,18 | 17,57 | 8,69 | 0,01 |
| 0,2 | 2 | 0,463 | 0,505 | 0,477 | 47,84 | 43,43 | 21,10 | 22,23 | 11,12 | 0,01 |
| 0,24 | 2,4 | 0,374 | 0,419 | 0,389 | 39,01 | 35,50 | 25,64 | 26,96 | 13,48 | 0,01 |
| 0,28 | 2,8 | 0,304 | 0,349 | 0,319 | 31,99 | 29,30 | 30,93 | 32,44 | 16,22 | 0,01 |
| 0,32 | 3,2 | 0,251 | 0,294 | 0,265 | 26,61 | 24,47 | 36,98 | 38,68 | 19,34 | 0,00 |
| 0,36 | 3,6 | 0,209 | 0,25 | 0,223 | 22,33 | 20,63 | 43,78 | 45,67 | 22,84 | 0,00 |
| Средняя осадка фундамента, см | 0,10 |
Нижняя граница сжимаемой толщи основания Hc = 0,35 м. Средняя осадка фундамента s = 0,10 см и относительная разность осадок Δs/Lu = 0,10/170 = 0,0006 не превышает предельных деформаций основания фундаментов здания с деревянными конструкциями на столбчатых фундаментах. Согласно п.6.8.10 при заложении фундаментов выше расчетной глубины промерзания пучинистых грунтов (малозаглубленные фундаменты) необходимо производить расчет деформаций морозного пучения грунтов основания с учетом касательных и нормальных сил морозного пучения.
Порядок расчета осадки фундаментов
Разрушение стен дома от неравномерной осадки фундамента
Любое строение со временем подвержено проседанию. Фундамент здания должен осесть в расчётных пределах. Если основание дома опустилось равномерно по всей площади опирания, то расчёт осадки фундамента произведён правильно.
В противном случае неравномерное проседание фундамента или свайного поля может привести к деформации несущих конструкций сооружения, что приведёт к повреждению строения.
Особенно велик риск неравномерного проседания оснований большой площади опирания, поэтому необходимо точно рассчитать допустимую осадку основания здания.
Применение метода
Методом послойного суммирования рекомендуется пользоваться, если нужно определить не только основные факторы осадок, но и вторичные или дополнительные, возникающие только в конкретных ситуациях.
Такие осадки часто возникают от соседних фундаментов, ведь с ростом нагрузки на площадку неизбежно возникают просадки почвы, особенно при использовании мощных тяжелых конструкций. Но тут часто проектировщики сталкиваются с проблемой именно создания этюдов осадок, ведь нужно четко определить по оси вертикали именно те силы, которые возникли от воздействия соседних оснований.
Расчет осадки ленточного фундамента
Расчетная схема методом послойного суммирования осадки ленточного фундамента
Для примера можно взять ленточный фундамент, который имеет ширину 120 см (b ) и глубину залегания 180 см (d). Он устроен на трех слоях грунта. Общее давление под подошвой на почву составляет 285 кПа.
Каждый слой грунта имеет следующие показатели:
По данным геодезической службы и топографической разведки, грунтовые воды в расчетном регионе расположены на глубине 3,8 метра, поэтому их влияние на основание можно считать практически нулевым.
Итак, учитывая, что метод послойного суммирования – это создание нескольких графических этюдов вертикального напряжения в грунтах, тогда пора их создать для расчета допустимой нагрузки на почву.
На поверхности земли σzg = 0, а вот на глубине 1,8 метра (уровень подошвы), σzg 0 = γ1d = 18,7Κ·1,8 = 33,66 кПа.
Теперь нужно рассчитать ординаты эпюры вертикального напряжения на стыках нескольких грунтовых слоев:
Также стоит учесть, что второй слой грунта насыщен водой, поэтому тут не обойтись без расчета допустимого давления столба воды:
Теперь внимание. В примере четко указано, что третий слой грунта принимает на себя не только давление двух верхних слоев, но и столба воды, поэтому этими параметрами пренебрегать нельзя
Таким образом, напряжение по подошве фундамента будет рассчитано по формуле:
Дополнительное давление под подошвой:
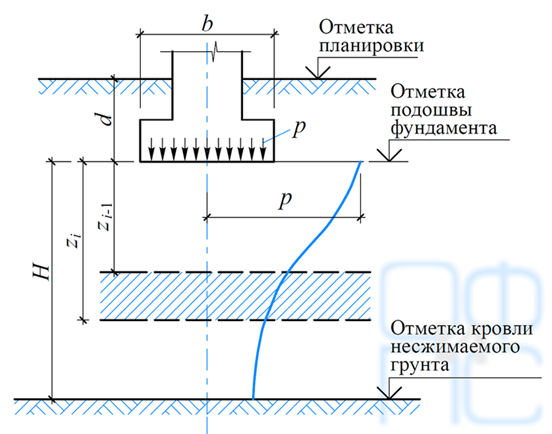
Далее все параметры этюдов напряжения нужно выбирать с расчетных таблиц СНиПа. В итоге получается, что осадка S1 первого слоя песка будет составлять:
Осадка более крупного песка:
Полная осадка фундамента, посчитанная методом послойного суммирования, будет составлять:
По параметрам, указанным в СНиП 2.02.01—83* для сооружений, возведенных на ленточных фундаментах с учетом указанных типов грунтов, параметр усадки соответствует норме.







Нюансы расчёта свайного фундамента
Некоторые особенности влияния нагрузки существуют для свайного фундамента. Поэтому рассмотрим пример вычисления.
Основные показатели, которые фигурируют в расчётах:
Данный пример предусматривает упрощённые вычисления.
Начнём с вопроса, каким должен быть радиус винтовых свай:
Расстояние между сваями также зависит от предполагаемой нагрузки. Если для постройки здания применяется газобетон или шлакоблоки, то шаг составляет 2 м, для более лёгких каркасных строений, не более 3 м.
Расчет осадки фундамента
Рассчитать осадку фундамента можно несколькими способами. Основным и самым проверенным способом определения конечной, полной осадки является метод суммирования осадок отдельных слоев. Для каждого из слоев необходимо определить свое значение степени деформации. Слои следует рассматривать в пределах определенной толщи грунта — в активной зоне, а деформации, которые происходят ниже этого уровня грунта, можно исключить. Метод суммирования осадок отдельных слоев можно использовать для определения любых осадок.
Также рассчитать осадку можно методом эквивалентного слоя, который позволяет определить осадку с учетом ограниченного бокового расширения. Эквивалентный слой — это такая толщина грунта, которая в условиях невозможности бокового расширения (при загруженности всей поверхности сплошной нагрузкой) дает осадку, которая равна по величине осадке фундамента, имеющего ограниченные размеры при нагрузке той же интенсивности. То есть, в этом случае пространственная задача расчета осадок может заменяться одномерной.
Расчёт осадки ленточного фундамента
Кроме метода послойного суммирования существуют различные методики определения величины проседания здания. При условиях отдельно стоящего строения с учётом сопротивления грунтового основания и других сил, только использование метода послойного суммирования будет наиболее верным расчётом.
Способ основан на создании эпюр напряжений в многослойной почве по каждой вертикальной оси.

Определение осадки ленточного фундамента производится с целью, чтобы:
Данная методика расчета определяет показатели основания по каждому сочетанию вертикальных осей, без учёта угловых переменных, используя периферийные значения и центральный показатель. Сделать это возможно при залегании по периметру основания строения равномерных структурных слоёв почвы.
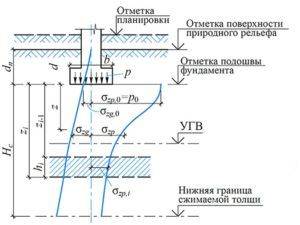
Обозначения по СНиП 2.02.01-83:
Ширина ленточного монолитного фундамента – 1200 мм (b), глубина заложения составит 1800 мм (d).
Видео «Расчёт сопротивления грунта»:
Пример определения величины осадки ленточного фундамента
Общая нагрузка от веса здания на почву составит 285000 кг•м−1•с−2. По каждому слою отмечают такие значения:

Результаты исследований грунта взяты в местном геолого-геодезическом управлении. Грунтовые воды на территории застройки находятся на расстоянии от поверхности земли 3800 мм. глубина залегания грунтовых вод такой величины не имеет значения даже для заглубленного фундамента здания. В этом случае воздействие грунтовых вод на осадку здания считают мизерным, то есть практически никаким.
Для нанесения графика эпюр и расчета критических нагрузок на грунт производят действия согласно СНиП 2.02.01-83.
В результате получают следующие показатели по каждому слою почвы: S1 = 11,5 мм; S2 = 13,7мм; S3 = 1,6 мм.
Суммарное проседание основания здания составит:
Расчёт осадки свайного основания
Определяют осадки свайного фундамента методом послойного суммирования.

Полный расчёт осадки свайного основания выполняется проектной организацией на протяжении от нескольких дней до 2-х недель. Проектировщики пользуются специальными компьютерными программами. Человеку, не имеющему специального образования, сделать это самостоятельно практически невозможно.
Произвести расчёт осадки свайного основания небольшого частного дома можно упрощённым способом, что под силу каждому застройщику.
Используя схемы расположения различных видов свай и расчётных формул, указанных в СП 24.13330.2011, можно определить как величину осадки одиночной сваи, так и степень проседания всего свайного поля.
Применяют различные методики определения величин осадки разных типов фундаментов, в основном, для крупных объектов промышленного и гражданского назначения.
Особенности расчёта нагрузки от типа основания
После того как определились с глубиной заложения фундамента необходимо рассчитать его ширину и другие параметры в зависимости от его вида. Перед тем, как рассчитать нагрузку на фундамент, определяемся с глубиной его заложения с учетом типа почвы. После этого стараемся определить остальные параметры. Для этого выполняем сбор нагрузок:





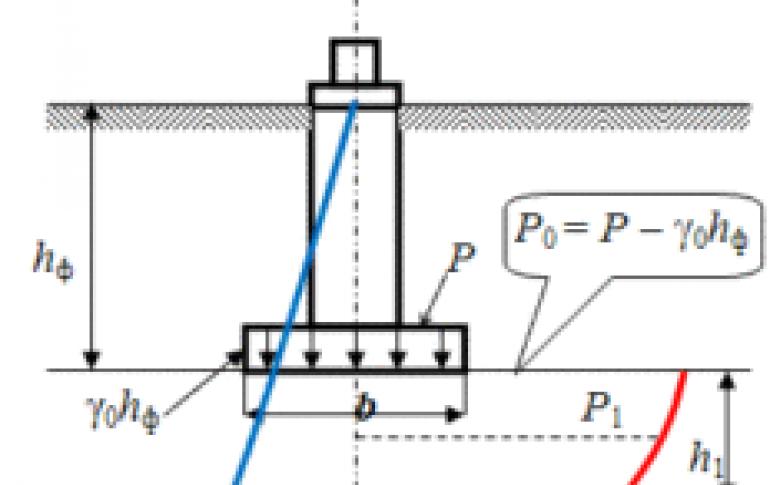



Определив все составляющие, необходимо высчитать количество материала и его вес. Полученные результаты умножают на показатель надежности статических нагрузок. Для каждого вида он различен:
Несколько советов по заложению фундамента
Многие, особенно начинающие строители, стремясь повысить качество и надёжность основания, допускают некоторые ошибки. Попробуем указать на основные нюансы:
Увеличивая высоту ленты основания можно добиться высокой степени жёсткости. Но данный показатель не всегда приводит к положительным результатам и уменьшает влияния на него нагрузок. Приходиться выполнять армирование фундаментов, которое повышает степень напряжения. Основанию необходимо придать гибкость, тем самым снизить коэффициент жёсткости.
Сложно выполнить расчёты деформаций от нагрузки, которые оказывают такие факторы, как морозное пучение или влияния грунтовых вод. Они могут со временем меняться. Поэтому лучше всего обращаться к специалистам для определения типа грунта и влияния климатических условий
Для предотвращения возникновения деформаций основания, следует обратить внимание на мероприятия по усилению, как самого фундамента, так и цоколя со стенами.
Для снижения воздействия на основание морозов в зимнее время и демисезонной влаги рекомендуется провести ряд мероприятий по утеплению и гидроизоляции. В том случае, когда они запланированы, то данный фактор надо учесть при расчёте нагрузки.
Если же к этой ответственной задаче приступили самостоятельно, то можно использовать специальные программы например Лира. Это компьютерная программа, которая позволяет выполнять строительные расчёты. Необходимо только правильно ввести все параметры, а техника посчитает и выдаст результат: расчёт фундамента при горизонтальной нагрузке, площадь подошвы и толщину подушки. К тому же, это отличная проверка самостоятельных расчётов. Не стоит забывать и об онлайн калькуляторах.
Предельно допустимые осадки фундаментов
На сегодняшний день отсутствуют убедительно обоснованная нормативная величина предельно допустимой дополнительной осадки зданий. Нормативные документы, как правило, не делают различия между первоначальной, полученной при строительстве, и дополнительной осадкой. Предельная средняя осадка кирпичного здания по документам составляет примерно 10-12 см.
Стоит отметить, что первоначальные осадки фундамента на однородном грунтовом основании равномерны по пятну застройки, поэтому даже при большой допустимой средней осадки (10-12 см), также удовлетворяются и требования в отношении неравномерности осадок. А, как известно, результатом неравномерности являются перекосы здания и возникновение трещин.
По стандартам, предельно допустимая осадка для зданий 1-ой категории технического состояния составляет 5 см, а для зданий 2-ой и 3-ей категории, уже имеющих деформации — 3 и 2 см.
Как показывают наблюдения, кирпичные здания 1-й и 2-й категории состояния при локальной дополнительной осадке 5 см могут получить серьезные повреждения. В стенах будут образовываться сквозные трещины, а при возникновении вертикальной трещины ее раскрытие сопоставимо с величиной осадки. Сдвиг плит сборных перекрытия при этом по площадкам опирания очень близок к предельному. В этом случае ремонт здания потребует выселения жильцов, выборочного усиления конструкции и восстановление внутреннего и наружного декора. При осадках 3 и 2 см потребуется ремонт меньшего объема. Так можно ли считать допустимой осадку фундамента 2-5 см? Конечно, если за критерий допустимости принимать отсутствие обрушения конструкций, и нельзя, если за критерий допустимости принимать отсутствие повреждений, которые требуют ремонта.
Исходные данные
Справка и принятые обозначения (нажать, чтобы открыть/закрыть)
В расчетах приняты следующие единицы измерений: тонны, метры.
Согласно СП 22.13330.2011 коэффициент к природному давлению для определения глубины сжимающей толщи принимается равным 0.5. Поправка коэффициента до значения 0.2 производится автоматически в том случае, когда нижняя граница сжимаемой толщи находится в слое грунта с модулем деформации E 2
Если в пределах глубины сжимаемой толщи залегает слой грунта с модулем деформации Е > 10000 т/м2, то она принимается до кровли этого грунта
При указании того, что слой обводнен, следующий слой без воды принимается водоупором с получением соответствующего скачка на эпюре природного давления. При этом обозначение слоя в виде водоупора в сводной таблице без подробной разбивки не выводится.
Ei — модуль деформации составляющего слой грунта, т/м2
kE,e,i — множитель к модулю деформации для перехода к модулю деформации по вторичной ветви (для сооружений нормального уровня ответственности допускается принимать равным 5.0)
γi — удельный вес грунта, т/м3
γs,i — удельный вес частиц грунта, т/м3
hi — толщига слоя грута, м
e — коэффициент пористости
Данные по первому слою приведены в качестве примера.
Расчетная нагрузка на основание Fz (т):
Коэффициент к природному давлению для определения глубины сжимающей толщи (от 0.2 до 1.0, по СП рекомендуется принимать 0.5):
Дополнительное давление к эпюре природного давления (т/м2):
Глубина заложения фундамента (м):
Ширина или диаметр фундамента (м):
Длина фундамента (м, только для прямоугольного типа):
Число слоев грунта (n ≤ 10):
Причины появления осадки фундамента
Состав грунта – это одна из самых главных причин, из-за которой возникает осадка основания дома. Почва делится на виды и каждый обладает своей прочностью. Самыми прочными видами почвенного покроя являются скальный грунт и дисперсная почва. По-другому эти почвы называют несвязными, так как они не сохранят в себе влагу.








В основе первого вида почвы лежат монолиты, а второй вид состоит из минерального зерна различного размера. Но существуют связные виды почву, они поглощают и сохраняют в себе влагу, поэтому основной составляющей этих типов почвенного покроя является глина, из-за чего слой грунта приобретает свойство подвижности и деформации. В холодное время года, содержащаяся в таких типах почвы влага, замерзает и слой грунта расширяется. Первая причина – связный слой грунта почвы. Вторая причина – особенности конструкции основания дома. Третья причина – неправильно распределенное давление стен на фундамент. При строительстве дома следует учитывать все эти факторы, чтобы в будущем не столкнуться с данной проблемой.
Данные по составу грунтового массива основания
Наличие воды:Без водыВодонасыщенныйВодоупор