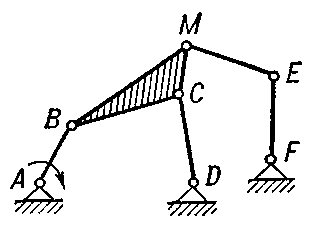
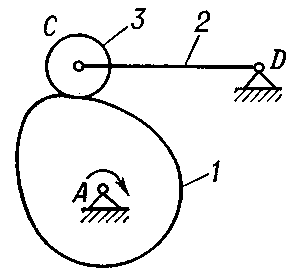
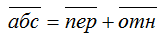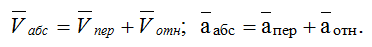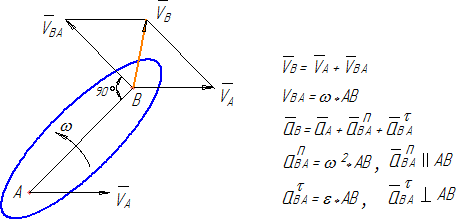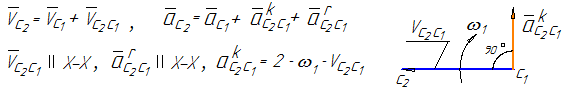ускорение 2го порядка в кинематике определяют для каких механизмов

Кинематика механизмов

Полезное

Смотреть что такое «Кинематика механизмов» в других словарях:

КИНЕМАТИКА МЕХАНИЗМОВ — раздел машин и механизмов теории, в котором изучается движение звеньев механизма независимо от приложенных к ним сил. Основные задачи: определение движения звеньев механизма по заданному движению одного или нескольких звеньев, называемые… … Большой Энциклопедический словарь

КИНЕМАТИКА МЕХАНИЗМОВ — (Engineering kinematics) часть прикладной механики, изучающая движение механизмов независимо от действующих сил. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь

кинематика механизмов — раздел машин и механизмов теории, в котором изучается движение звеньев механизма независимо от приложенных к ним сил. Основные задачи: определение движения звеньев механизма по заданному движению одного или нескольких звеньев, называется… … Энциклопедический словарь

кинематика механизмов — Раздел теории механизмов, в котором изучается движение звеньев механизма независимо от приложенных к ним сил … Политехнический терминологический толковый словарь

Кинематика (значения) — Кинематика совокупность дисциплин, изучающая математическое описание движения. Кинематика в физике раздел механики, изучающий математическое описание движения идеализированных объектов: Кинематика точки; Кинематика твёрдого тела;… … Википедия

Кинематика — Кинематика совокупность дисциплин, изучающая математическое описание движения. Кинематика в физике раздел механики, изучающий математическое описание движения идеализированных объектов: Кинематика точки; Кинематика твёрдого тела; Кинематика… … Википедия

КИНЕМАТИКА — (от греч. kinema, род. п. kinematos движение), раздел механики, посвящённый изучению геом. св в движений тел, без учёта их масс и действующих на них сил. Методы и зависимости, устанавливаемые в К., используются при кинематич. исследованиях… … Физическая энциклопедия

Кинематика — (от греч. kínema, родительный падеж kinematos движение) раздел механики (См. Механика), посвященный изучению геометрических свойств движений без учета их масс и действующих на них сил. Излагаемое ниже относится к К. движений,… … Большая советская энциклопедия

КИНЕМАТИКА — ЦИНЕМАТИКА или КИНЕМАТИКА (греч.). Учение с движениях, независимо от рассмотрения сил, производящих эти движения. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КИНЕМАТИКА (греч.). Наука, изучающая состояние,… … Словарь иностранных слов русского языка

КИНЕМАТИКА — [от греч. kinema (kinematos) движение] раздел механики, в к ром изучаются геом. св ва механич. движения тел без учёта действующих на них сил. К. механизмов раздел машин и механизмов теории, в к ром изучается движение звеньев механизма независимо… … Большой энциклопедический политехнический словарь

Источник

iSopromat.ru

Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов в теории механизмов и машин.

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное — движение данной точки относительно той, движение которой принято за переносное:

Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

Планы скоростей и ускорений обладают следующими свойствами:

При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:

1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).

В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.

Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;

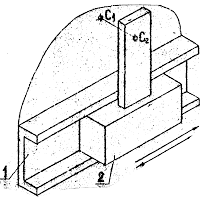
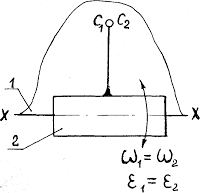
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).

Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С₁, принадлежащей этой направляющей.

Движение точки С₁ принимается в качестве переносного. Движение точки С₂, принадлежащей ползуну, относительно точки С₁ получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С₁ и С₂ совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).

Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.

Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.

Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов

Источник

Тема 1.6. Основные понятия кинематики

§1. Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Рис.1. Система отчета

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Рис.2. Радиус-вектор

Рис.3. Координаты точки М

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движе­нии все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Видео-урок «Механическое движение»

§2. Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Рис.4. Движение точки М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Рис.5. Движение точки М

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).

§3. Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.

Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.

Источник

Ускорение 2го порядка в кинематике определяют для каких механизмов

Геометрические и кинематические характеристики механизмов.

Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты.

Геометрические и кинематические характеристики механизма

Рис. 3.1

Схема механической системы

Рис. 3.2

Рис. 3.3

Функции положения в механизмах

Рис. 3.4

Методы геометро-кинематического исследования механизмов

Связь кинематических и передаточных функций

Линейные скорости и ускорения

Угловые скорости и ускорения

Так как данные формулы получены как производные от скалярных величин, то при операциях с векторными величинами они применимы только для проекций этих величин на оси координат.

1. Метод проекций векторного контура. (Рычажные механизмы).

Рассмотрим простейший кулисный механизм.

Рис. 3.5

Заменим кинематическую схему механизма эквивалентным векторным контуром

Тогда уравнение замкнутости векторного контура запишется:

1. 1. Задача о положениях звеньев механизма

Рис. 3.6

Проецируем векторный контур на оси координат и получаем координаты точки В механизма:

1. 2. Задача о первых кинематических передаточных функциях механизма

Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим

1. 3. Задача о вторых передаточных функциях механизма.

Вторично продифференцируем уравнения проекций векторного контура по обобщенной координате и получим

Цикловые кинематические (геометрические) диаграммы для кулисного механизма.

Циклом называется период времени или изменения обобщенной координаты по истечении которого все параметры системы принимают первоначальные значения. Поэтому значения величин в начале и в конце цикла одинаковы. 2.Метод центроид (Зубчатые передачи). Центроидой (полоидой) называется геометрическое место центров (полюсов) относительного вращения в системах координат связанных со звеньями механизма. В зубчатом механизме при передаче движения центроиды колес перекатываются друг по другу без скольжения. Схема зубчатого механизма Рис. 3.8 где: Откуда: Функция положения для выходного звена зубчатой передачи Вторая передаточная функция для выходного звена зубчатой передачи Механизм зубчатой передачи не является цикловым механизмом, так как угловое перемещение выходного звена увеличивается при увеличении углового перемещения входного. Поэтому кинематические диаграммы построим только для одного оборота входного звена. Диаграммы функции положения и передаточных функций для зубчатой передачи. Рис. 3.9 Рис. 3.10 Рис. 3.11 m S = y hb / h B мм/м; m f = b / f р мм/рад; m t = b/t р мм/с; m Vq = k 1 * m S / m f мм/м; m aq = k 2 * m Vq / m f мм/м; 4. Метод преобразования координат (Манипуляторы) При использовании метода преобразования координат задача о положении выходного звена решается путем перехода из системы в которой это положение известно в систему в которой его требуется определить. Переход от системы к системе осуществляется перемножением матриц перехода в соответствующей последовательности. 4. 1. Формирование матрицы перехода для плоских механизмов. Рис. 3.12 Координаты точки М в системе i через координаты этой точки в системе j определятся следующей системой уравнений: Тогда векторы столбцы координат точки М и матрица перехода из системы j в систему i Векторное уравнение перехода из системы j в систему i Пример применения метода преобразования координат для плоского трехподвижного манипулятора: Рис. 3.13 5. Экспериментальный метод кинематического исследования. Рис. 3.14 В этой экспериментальной установке: для измерения перемещения выходного звена используется потенциометрический датчик перемещения, в котором пропорционально положению движка потенциометра изменяется его сопротивление; для измерения скорости выходного звена используется идукционный датчик скорости, в котором напряжение на концах катушки движущейся в поле постоянного магнита пропорционально скорости катушки; Передаточные функции механизмов с несколькими подвижностями (W>1). Рассмотрим простой двухподвижный манипулятор Рис. 3.15 Функция положения для выходного звена этого механизма является функцией двух переменных и ее производная определится как производная функции двух переменных: Контрольные вопросы к лекции 3. Источник Основы механики для чайников. Часть 1: Кинематика В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи. Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам. Траектория, радиус-вектор, закон движения тела Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел. Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно. Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении. Радиус-вектор – вектор, задающий положение точки в пространстве. Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени. Перемещение и путь Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения. В системе СИ перемещение и длина пути измеряются в метрах. Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора. Скорость и ускорение Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной. Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории. В системе СИ скорость измеряется в метрах в секунду Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение. Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное. Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка. Здесь R – радиус окружности, по которой движется тело. Закон равноускоренного движения Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x. Производная по скорости от времени даст значение ускорения a, которое является константой. Пример решения задачи Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше. Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени. Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины. Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее. Источник ← Акцептировано что это значит Антижизнь лига справедливости что → Вам также понравится узи органов брюшной полости это какие органы 10.10.202319.07.2022 admin 0 у какого дерева нет годичных колец 05.10.202318.07.2022 admin 0 Как называется мультик про пингвинов 07.10.202315.07.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email *